2006届高三期末三校（国光中学、德化一中、晋江一中）
联考文科数学试卷
姓名：_________ 学号：__________ 班次：__________ 成绩：_________
卷Ⅰ 选择题
1、已知集合
，则有（ ）
A、M∪N=M B、M∪N=N C、M∩N=M D、M∩N
2、过点A（1，2）且在两坐标轴上的截距的绝对值相等的直线共有（ ）条
A、1 B、2 C、3 D、4
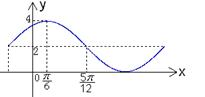3、已知函数
的一部分图象如右图所示，如果
，则（ ）
A、
B、
C、
D、
4、若直线
到直线
的角为
，则实数
等于（ ） A、0 B、
C、0或 D、0或
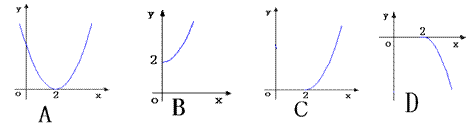
5、函数f（x）=
+2（x
0）的反函数f
（x）的图象是（ ）
6、已知双曲线是以椭圆
的两个顶点为焦点，以椭圆的焦点为顶点，那么双曲线的方程为（ ）
A、
B、
C、
D、
7、把一个函数的图像按
=（
，2）平移后得到的图像的函数为y=sin（x＋）＋2，那么原来函数的解析式为（ ）
A、y=sinx B、y=cosx C、y=sinx＋2 D、y=cosx＋4
8、在以下关于向量的命题中，不正确的是（ ）
A、若向量
＝（x，y），向量
＝（－y，x）(x、y≠0)，则⊥
B、
C、△ABC中，
和
的夹角等于
－A
D、点G是△ABC的重心，则
+
－
=
9、若等差数列中，前3项和为34，后3项和为146，所有项和为390，则数列共有（ ）
A、13项 B、12项 C、11项 D、10项
10、一张报纸，其厚度为a，面积为b，现将此报纸对折，（即沿对边中点的连线折叠）7次，这时报纸的厚度和面积分别为（ ）
A、
B、
C、
D、
11、已知
，
，则x，y的大小关系是（ ）A、
Ｂ、
Ｃ、
Ｄ、不能确定
12、一个圆心在曲线
上的动圆恒过点(0，1)，且恒与定直线l相切，则直线l的方程为（ ）
A、x＝l
B、x＝
C、y＝－1
D、y＝－
卷Ⅱ 非选择题
13、设集合
，
， 若
，则实数
的取值范围是_____________
14、已知
，则不等式
的解集是__________
15、给出下列命题：
①函数
是偶函数；
②函数
在闭区间
上是增函数；
③直线
是函数
图象的一条对称轴；
④将函数
的图象向左平移
单位，得到函数
的图象。
其中正确的命题的序号是_____________
16、
的三顶点为
（2，4）、
（－1，2）、
（1，0），则的内部可用二元一次不等式组表示为
17、（本题满分12分）已知
，求实数a的取值范围
18、（本题满分12分）设正数数列{
}的前n项和Sn满足
。
（1）求数列{}的通项公式；
（2）设
的前n项和为Tn，求证：
19、（本题满分12分）在中，a、b、c分别是角A、B、C的对边，且
。
（1）求∠A的度数；
（2）若
，求
的最大值，并判断当取得最大值时的形状。
20、（本题满分12分）已知向量
，
，
满足
，且
，
。
（1）求向量；
（2）若映射
①求映射f下（1，2）原象；
②若将（x、y）作点的坐标，问是否存在直线l使得直线l上任一点在映射f的作用下，仍在直线上，若存在求出l的方程，若不存在说明理由
21、（本题满分12分）已知双曲线
的两条渐近线过坐标原点，且与以点
为圆心，
为半径的圆相切，双曲线的一个顶点
与点关于直线
对称，设直线
过点，斜率为
。
（1）求双曲线的方程；
（2）当
时，若双曲线的上支上有且只有一个点到直线的距离为
，求斜率的值和相应的点的坐标。
22、（本题满分14分）已知函数
是定义域为R的奇函数，且它的图象关于直线x＝1对称。
（1）求
的值；
（2）证明函数是以4为周期的周期函数；
（3）若
，求x∈[－1，3]时，函数的解析式，并求方程
在实数集上的解集。
2005年秋季国光中学、晋江一中、德化一中三校联考
高三年级数学（文科）考试卷参考解答
一、选择题：（本题共12题，每题5分，共60分请将唯一正确答案的编号填入答题卡的相应位置上）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | C | A | C | B | B | D | A | C | A | C |
二、填空题：（本题共4题，每题4分，共16分，请将你认为正确的答案填写在答题卡相应位置的横线上）
13、m
-1 14、
15、①③ 16、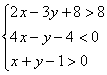
三、解答题：（本大题共6小题，共74 分，解答应写出文字说明．证明或演算步骤）
17、由
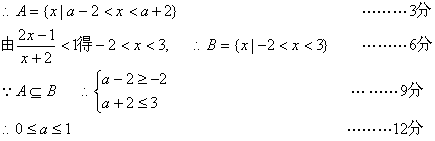
18、解：（1）
①
②
…………2分
①－②得
，
整理得
…………4分
是等差数列。…………6分
又
…………8分
（2）
……10分
…………12分
19、解：（1）由4sin2
－cos2A＝
及A＋B＋C＝180°，
得2［1－cos(B＋C)］－2cos2A＋1＝，…………………2分
4(1＋cosA)－4cos2A＝5。…………………4分
∴4cos2A－4cosA＋1＝0，∴cosA＝
。
∵0°＜A＜180°，∴A＝60°。…………………6分
（2）由余弦定理得：cosA＝
。
∵cosA＝，∴＝ ，且a＝…………………8分
∴
又
∴
∴
当
，即
时，bc取得最大值3，…………………11分
此时，a=，故bc取得最大值时，△ABC是正三角形。………………12分
20、解：（1）设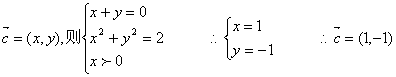
………………4分
（2）①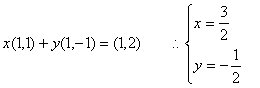
………………6分
②假设l存在，设其方程为
………………7分
………………8分
点
………………9分
即（1+k）
………………10分
………………11分
………………12分
21、解：（1）设双曲线的渐进线方程是
与圆
相切，………………1分
渐进线方程为
，………………3分
又双曲线的一个顶点关于的对称点为
双曲线的方程为
。………………6分
（2）直线
，………………7分
设在上方与平行且相距的直线
的直线方程是
………………8分
由
的方程是
代入，………………9分
解得（Ⅰ）当
时方程只有一组解，符合题意。此时
（Ⅱ）当
时，由与有且只有一个公共点，
得
综上所述：
……………12分
22、（1）解：∵ 函数f（x）是奇函数，∴f（－x）＝－f（x）………………2分
令x＝0，f（0）＝－f（0），2f（0）＝0，
∴ f（0）＝0…………………………4分
（2）证明：∵ 函数f（x）是奇函数，∴f（x）＝－f（－x）
∵函数f(x)的图象关于直线x=1对称，所以f(1+x)=f(1-x) ………………………6分
∴ f（x）是以4为周期的周期函数。…………………………9分
（3）解：
…………………………12分
在
时，f(x)=1的解为x=1，又f(x)是周期为4的函数，∴f(x)=1在R上的解集为
…………………………14分