高三数学第二次月考试题 2005.10.25
姓名:___________总分:____________
一![]() 选择题(每小题5分,共60分)
选择题(每小题5分,共60分)
1![]() 下列四组函数中,表示同一函数的是( )
下列四组函数中,表示同一函数的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2![]() (文科学生做)“
(文科学生做)“![]() ”的一个充分条件是( )
”的一个充分条件是( )
A. ![]() B.
B. ![]() C.
C.![]() D.
D.![]()
*2![]() (理科学生做)已知
(理科学生做)已知![]() , 在下列不等式中成立的一个是( )
, 在下列不等式中成立的一个是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3![]() (文科学生做)二次函数
(文科学生做)二次函数![]() 中,若
中,若![]() ,则其图象与
,则其图象与![]() 轴交点个数是( )
轴交点个数是( )
A.1个 B.2个 C.没有交点 D.无法确定
*3![]() (理科学生做)已知一个二次函数的对称轴为x=2,它的图象经过点(2, 3),且与某一次函数的图象交于点(0, -1),那么已知的二次函数的解析式是( )
(理科学生做)已知一个二次函数的对称轴为x=2,它的图象经过点(2, 3),且与某一次函数的图象交于点(0, -1),那么已知的二次函数的解析式是( )
A . f (x)=-x2-4x-1 B. f (x)=-x2+4x+1
C. f (x)=-x2+4x-1 D. f (x)=x2-4x+1
4![]() 函数f (x)=4x2-mx+5,当x∈(-2, +∞)时是增函数,当x∈(-∞, -2)时是减函数,则f (1)的值是( )
函数f (x)=4x2-mx+5,当x∈(-2, +∞)时是增函数,当x∈(-∞, -2)时是减函数,则f (1)的值是( )
A -7 B 25 C 1 7 D 1
5![]() 命题p:若a
命题p:若a![]() b∈R,则a+b>1是a+b>1的充分而不必要条件;命题q:函数y=
b∈R,则a+b>1是a+b>1的充分而不必要条件;命题q:函数y=![]() 的定义域是(-∞,-1
的定义域是(-∞,-1![]() ∪[3,+∞
∪[3,+∞![]() ,则(
)
,则(
)
(A)“p或q”为假 (B)“p且q”为真 (C) p真q假 (D) p假q真
6![]() (文科学生做)如果奇函数
(文科学生做)如果奇函数![]() 在
在![]() 上是增函数且最小值是5,那么
上是增函数且最小值是5,那么![]() 在
在![]() 上是( )
上是( )
A.增函数且最小值是![]() B.增函数且最大值是
B.增函数且最大值是![]() .
.
C.减函数且最小值是![]() D.减函数且最大值是
D.减函数且最大值是![]()
*6![]() (理科学生做)函数
(理科学生做)函数![]() 在
在![]() 上是增函数,那么实数
上是增函数,那么实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7![]() 设f(x)=
设f(x)=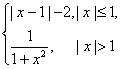 ,则f[f(
,则f[f(![]() )]= ( )
)]= ( )
A.![]() B.
B.![]() C.-
C.-![]() D.
D.
![]()
8![]() 已知实数a, b满足等式
已知实数a, b满足等式![]() 下列五个关系式①0<b<a ②a<b<0
下列五个关系式①0<b<a ②a<b<0
③0<a<b ④b<a<0 ⑤a=b 其中不可能成立的关系式有( )
A.1个 B.2个 C.3个 D.4个
9![]() (文科学生做)函数
(文科学生做)函数![]() 的图象必不过( )
的图象必不过( )
 A.第一象限 B.第二象限 C.第三象限 D.第四象限
A.第一象限 B.第二象限 C.第三象限 D.第四象限
*9![]() (理科学生做)
(理科学生做)![]() 是
是![]() 的导函数,
的导函数,![]() 的图象如图所示,
的图象如图所示,
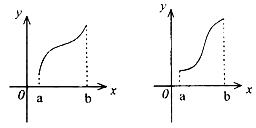
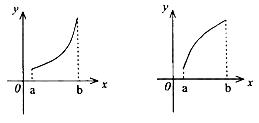 则
则![]() 的图象只可能是( )
的图象只可能是( )
A B C D
10![]() 已知函数
已知函数![]() 有负值,那么实数
有负值,那么实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B.![]() C.
C. ![]() D.
D.![]()
11![]() 下列各图象表示的函数中,存在反函数的只能是( )
下列各图象表示的函数中,存在反函数的只能是( )
A 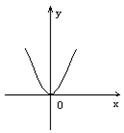 B
B 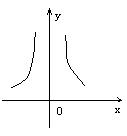 C
C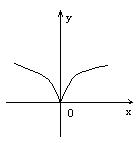 D
D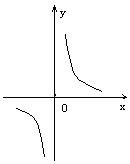
12![]() (文科学生做)若函数
(文科学生做)若函数![]() 是定义在R上的偶函数,在
是定义在R上的偶函数,在![]() 上是减函数,且
上是减函数,且![]() ,则使得
,则使得![]() 的x的取值范围是( )
的x的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.(-2,2)
D.(-2,2)
*12![]() (理科学生做)设
(理科学生做)设![]() 的值为( )
的值为( )
A![]() 1 B
1 B![]() -1 C
-1 C![]()
![]() D
D![]()
![]()
二![]() 填空题 (每小题4分,共16分)
填空题 (每小题4分,共16分)
13![]() 已知
已知![]() ,则实数
,则实数![]()
![]()
14![]() 函数
函数![]() 的图象与其反函数的图象的交点的坐标为______________
的图象与其反函数的图象的交点的坐标为______________
15![]() (文科学生做)
若
(文科学生做)
若![]() ,且
,且![]() 恒成立,则
恒成立,则![]() 的取值范围是_______________
的取值范围是_______________
*15![]() (理科学生做)若
(理科学生做)若![]() ,则
,则![]() 的最小值为________________
的最小值为________________
16![]() (文科学生做)定义运算
(文科学生做)定义运算![]() ,例如1
,例如1![]() 2=1, 则
2=1, 则![]() 的取值范围是________
的取值范围是________
*16![]() (理科学生做)设
(理科学生做)设![]() 表示不大于
表示不大于![]() 的最大整数,如
的最大整数,如![]() ,
,
则使 [![]() ]=3成立的
]=3成立的![]() 的取值范围是_____________
的取值范围是_____________
三![]() 解答题
解答题
17. (本题满分12分)
已知集合![]() ,
,
集合![]() 满足
满足![]() ,求实数
,求实数![]() 的值
的值![]()
18![]() (本题满分12分)设函数
(本题满分12分)设函数![]() ,函数
,函数
![]()
![]() 的图像过点A(
的图像过点A(![]() )及B(
)及B(![]() ),
),
(1)求![]() 和
和![]() 的表达式;
的表达式;
(2)求函数![]() 的定义域和值域
的定义域和值域
19![]() (本题满分12分)某种汽车购买时费用为10万元,每年应交保险费
(本题满分12分)某种汽车购买时费用为10万元,每年应交保险费![]() 养路费及汽油合计为9千元,汽车维修费平均为:第一年2千元,第二年4千元,第三年6千元,…依次成等差数列逐年递增.问:这种汽车使用多少年报废最合算(即使用多少年的平均费用最少)?
养路费及汽油合计为9千元,汽车维修费平均为:第一年2千元,第二年4千元,第三年6千元,…依次成等差数列逐年递增.问:这种汽车使用多少年报废最合算(即使用多少年的平均费用最少)?
20![]() (本题满分12分)已知函数
(本题满分12分)已知函数![]() ,
,![]() (
(![]() 为正常数),且函数
为正常数),且函数![]() 与
与![]() 的图象在
的图象在![]() 轴上的截距相等
轴上的截距相等![]() ⑴求
⑴求![]() 的值;
的值;
⑵求函数![]() 的单调递增区间
的单调递增区间![]()
21![]() (文科学生做(本题满分12分)已知函数
(文科学生做(本题满分12分)已知函数![]() 是函数
是函数![]() 图像上的点
图像上的点![]() (Ⅰ)求实数
(Ⅰ)求实数![]() 的值及函数
的值及函数![]() 的表达式
的表达式![]()
(Ⅱ)将函数![]() 的图像沿
的图像沿![]() 轴向右平移3个单位,得到函数
轴向右平移3个单位,得到函数![]() 的图像
的图像![]() 求函数
求函数![]() 的最小值
的最小值![]()
*21![]() (理科学生做)(本题满分12分)设函数
(理科学生做)(本题满分12分)设函数![]()
(1)求函数![]() 的极大值和极小值;
的极大值和极小值;
(2)当![]() ∈[
∈[![]() ]时,不等式
]时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
22![]() (文科学生做) (本小题满分14)已知函数
(文科学生做) (本小题满分14)已知函数![]() 的定义域为
的定义域为![]() ,且满足条件:①
,且满足条件:①![]() ,②
,②![]() ③当
③当![]()
⑴求证:函数![]() 为偶函数;
为偶函数;
⑵讨论函数![]() 的单调性;
的单调性;
⑶求不等式![]() 的解集
的解集![]()
*22![]() (理科学生做) (本小题满分14)设函数
(理科学生做) (本小题满分14)设函数![]() 的定义域是R,对于任意实数
的定义域是R,对于任意实数![]() ,恒有
,恒有
![]()
(1)求证:![]()
(2)判断函数![]() 在R上的单调性;
在R上的单调性;
(3)设集合![]() ,集合
,集合![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围
的取值范围![]()
参考答案
一![]() 选择题: DC(D)B©BD B(A)BBA(D)A DD(D)
选择题: DC(D)B©BD B(A)BBA(D)A DD(D)
二![]() 填空题:(13)0,2 (14)(0,0),(1,1)
填空题:(13)0,2 (14)(0,0),(1,1)
(15)(文科)![]() ,(理科)
,(理科)![]()
(16)(文科)(0,1],(理科)![]()
三![]() 解答题:
解答题:
17![]() a=-2
a=-2
18![]() (1)
(1)![]()
(2)定义域为(-1,3)
值域为(-∞,2]
19![]() 使用10年最合算
使用10年最合算
20![]() 解:⑴由题意,
解:⑴由题意,![]() ,
,![]() 又
又![]() ,所以
,所以![]()
![]()
⑵![]()
当![]() 时,
时,![]() ,它在
,它在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,它在
,它在![]() 上单调递增
上单调递增![]()
21![]() (文科)(1)由题知,点
(文科)(1)由题知,点![]()
所以 ![]()
(2)![]()
=![]() 当且仅当x=3时,取“=”
当且仅当x=3时,取“=”
所以F(x)的最小值为![]()
(理科)解(1)∵f′(x)=-x2+4ax-3a2=-(x-3a)(x-a),由f′(x)>0得:a<x<3a
由f′(x)<0得,x<a或x>3a,
则函数f(x)的单调递增区间为(a, 3a),单调递减区间为(-∞,a)和(3a,+∞)
列表如下:
| x | (-∞,a) | a | (a, 3a) | 3a | (3a,+ ∞) |
| f′(x) | — | 0 | + | 0 | — |
| f(x) |
| - |
| b |
|
∴函数f(x)的极大值为b,极小值为-![]() a3+b…………………………(6分)
a3+b…………………………(6分)
(2)![]() 上单调递减,因此
上单调递减,因此![]()
∵不等式f′(x)≤a恒成立,
![]()
即a的取值范围是![]() ……………………………………(12分)
……………………………………(12分)
22![]() (文科)1)在①中令x=y=1, 得f(1)= f(1)+ f(1)
(文科)1)在①中令x=y=1, 得f(1)= f(1)+ f(1)![]() f(1)=0,
f(1)=0,
令x=y=-1, 得f(1)=
f(-1)+ f(-1)![]() f(-1)=0,
f(-1)=0,
再令y=-1, 得f(-x)= f(x)+ f(-1)![]() f(x), ∴f(x)为偶函 数;
f(x), ∴f(x)为偶函 数;
(2)在①中令![]()
先讨论![]() 上的单调性, 任取x1
上的单调性, 任取x1![]() x2,设x2>x1>0,
x2,设x2>x1>0,
![]()
由③知:![]() >0,∴f(x2)>f(x1), ∴f(x)在(0,+∞)上是增函数,
>0,∴f(x2)>f(x1), ∴f(x)在(0,+∞)上是增函数,
∵偶函数图象关于y轴对称 ,∴f(x)在(-∞,0)上是减函数;
(3)∵f[x(x-3)]= f(x)+ f(x-3)≤2, 由①![]() ②得2=1+1= f(2)+ f(2)=
f(4)= f(-4),
②得2=1+1= f(2)+ f(2)=
f(4)= f(-4),
1)若x(x-3)>0 , ∵f(x)在(0,+∞)上为增函数,
由f[x(x-3)] ≤f(4) 得

2)若x(x-3)<0, ∵f(x)在(-∞,0)上为减函数;
由f[x(x-3)] ≤f(-4)得 ![]()
∴原不等式的解集为:
![]()
![]()
(理科)解:⑴f(m+n)=f(m)f(n),令m=1,n=0,则f(1)=f(1)f(0),且由x>0时,0<f(x)<1,∴f(0)=1;设m=x<0,n=-x>0,∴f(0)=f(x)f(-x),∴f(x)=![]() >1
>1![]()
⑵设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1,∴f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)f(x1)-f(x1)=f(x1)[f(x2-x1)-1]<0,∴f(x)在R上单调递减![]()
⑶∵f(x2)f(y2)>f(1),∴f(x2+y2)>f(1),由f(x)单调性知x2+y2<1,又f(ax-y+2)=1=f(0),
∴ax-y+2=0,又A∩B=![]() ,∴
,∴![]() ,∴a2+1≤4,从而
,∴a2+1≤4,从而![]()
![]()