2006届高三起点考试数学试卷(广东卷)
命 题:江苏宿迁中学 陈炳堂 湖北团风中学 王志明
审 定:黄冈市文海教科所
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟![]()
参考公式:
如果事件A![]() B互斥,那么
B互斥,那么
![]()
![]() 球的表面积公式
球的表面积公式
如果事件A![]() B相互独立,那么
B相互独立,那么
![]()
![]() 球的体积公式
球的体积公式
如果事件A在一次试验中发生的概率是P,那
![]()
么n次独立重复试验中恰好发生k次的概率 其中R表示球的半径
第Ⅰ卷(选择题,共50分)
一、选择题:本大题共有10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的![]()
1.![]()
![]() C
1
D -1
C
1
D -1
2.![]()
A![]() 0 B
0 B![]()
![]() C
C ![]() 1 D
1 D![]() -1
-1
3.“直四棱柱ABCD—A1B1C1D1各条棱长相等”是“直四棱柱ABCD—A1B1C1D1为正方体”的
A![]() 充分但不必要条件
B
充分但不必要条件
B![]() 必要但不充分条件
必要但不充分条件
C![]() 充要条件
D
充要条件
D![]() 既不充分也不必要条件
既不充分也不必要条件
4.设函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域是
的定义域是
A![]() (2,3] B
(2,3] B![]() [2,3] C
[2,3] C![]()
![]() D
D![]() 不存在函数
不存在函数![]()
5.点P从(0,1)出发,沿单位圆![]() 逆时针方向运动
逆时针方向运动![]() 弧长到达Q点,则Q点的坐标为
弧长到达Q点,则Q点的坐标为
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
6.![]() ,可以推出
,可以推出
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
7.函数![]() 的初相是
的初相是
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
8.如果函数![]() ,那么
,那么![]() 的图象是
的图象是
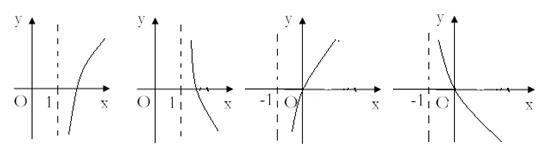
A B C D
9![]() 设椭圆
设椭圆![]() ,双曲线
,双曲线![]() ,抛物线
,抛物线![]() 的离心率分别为
的离心率分别为![]() ,
,![]() ,
,![]() ,则
,则
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]() 与
与![]() 的大小关系不能确定
的大小关系不能确定
10.已知向量![]() 且
且![]() ;a=3,b=4,c=5
;a=3,b=4,c=5![]() 设
设![]() 的夹角为
的夹角为![]() ,
,![]() 的夹角为
的夹角为![]() ,
,![]() 的夹角为
的夹角为![]() ,则的大小关系是
,则的大小关系是
A![]()
![]() <
<![]() <
<![]() B
B![]()
![]() <
<![]() <
<![]() C
C![]()
![]() <
<![]() <
<![]() D
D![]()
![]() <
<![]() <
<![]()
第Ⅰ卷答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
第Ⅱ卷(非选择题,共100分)
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在横线上![]()
11.不等式![]() 的解集为_______________________________
的解集为_______________________________![]()
12.兄弟三人同在某公司上班,该公司规定,每位职工可以在每周7天中任选2天休息(如选定星期一![]() 星期三),以后不再改动,则每位职工休息的种数为_____________;他们三兄弟同时工作
星期三),以后不再改动,则每位职工休息的种数为_____________;他们三兄弟同时工作![]() 同时休息的概率是_______________
同时休息的概率是_______________![]()
13![]() 一个正方体的全面积为
一个正方体的全面积为![]() ,它的顶点都在同一个球面上,则这个球的体积是__________
,它的顶点都在同一个球面上,则这个球的体积是__________![]()
14![]() 某班一周内每天做一次数学小练习,每次练习都是由15个选择题构成,每小题10分,满分为150分,且每个选择题有4个选项,其中有且有一个选项是正确答案
某班一周内每天做一次数学小练习,每次练习都是由15个选择题构成,每小题10分,满分为150分,且每个选择题有4个选项,其中有且有一个选项是正确答案![]() 学生A选对任一题的概率为
学生A选对任一题的概率为![]() ,学生B则每题都从4个选项中随机地选择一个,那么学生A
,学生B则每题都从4个选项中随机地选择一个,那么学生A![]() B在一周每次的分数期望分别为__________________
B在一周每次的分数期望分别为__________________![]()
三、解答题:本大题共6小题,共80分![]() 解答应写出文字说明,证明过程或演算步骤
解答应写出文字说明,证明过程或演算步骤![]()
15.(本小题满分12分) 设![]()
(1)
求![]()
(2)
若![]()
![]()
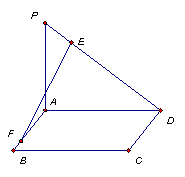
16(本小题满分14分)如图,ABCD是矩形,PA⊥平面ABCD,PA=AD=![]() ,AB=
,AB=![]() ,E是线段PD上的点,F是线段AB上的点,且
,E是线段PD上的点,F是线段AB上的点,且![]()
![]()
(1)![]() 时,求直线EF与平面ABCD所成的角的正弦值;
时,求直线EF与平面ABCD所成的角的正弦值;
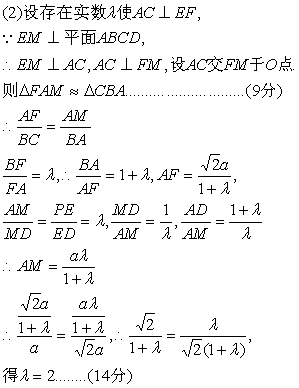
(2)是否存在实数![]() ,使AC⊥EF?若存在,试求出
,使AC⊥EF?若存在,试求出![]() 的值
的值![]() 若不存在,说明理由
若不存在,说明理由![]()
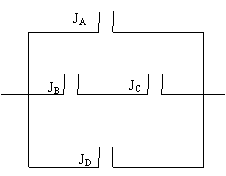
17.(本小题满分14分)在一段线路中有4个自动控制的常用开关![]() 如图连接在一起
如图连接在一起![]() 假定在2005年9月份开关
假定在2005年9月份开关![]() 能够闭合的概率都是0
能够闭合的概率都是0![]() 7,开关
7,开关![]() 能够闭合的概率都是0
能够闭合的概率都是0![]() 8
8![]()
 (1)求
(1)求![]() 所在线路能正常工作的概率;
所在线路能正常工作的概率;
(2)计算在9月份这段线路能正常工作的概率![]()
18.(本小题满分12分)已知抛物线![]() 的焦点为F,A是抛物线上一点,且纵坐标为4,A到抛物线准线的距离为5
的焦点为F,A是抛物线上一点,且纵坐标为4,A到抛物线准线的距离为5![]()
(1)求抛物线的方程;
(2)过点M(2,-1)作抛物线的两条切线分别交于B![]() C两点
C两点![]() 求证:
求证:![]()
19.(本小题满分14分)已知函数![]()
(1)求函数![]() 的值域;
的值域;
(2)设函数![]() 的定义域为D,若对任意的
的定义域为D,若对任意的![]() ,都有
,都有![]()
成立,则称函数![]() 为“标准函数”,否则称为“非标准函数”
为“标准函数”,否则称为“非标准函数”![]() 试判断函数
试判断函数![]() 是否为“标准函数”,如果是,请给出证明;如果不是,请说明理由
是否为“标准函数”,如果是,请给出证明;如果不是,请说明理由![]()
20.(本小题满分14分)已知数列{![]() }满足
}满足![]() ,且
,且![]()
(1)求证:数列{![]() }是等差数列;
}是等差数列;
(2)求数列{![]() }的通项公式;
}的通项公式;
(3)设数列{![]() }的前
}的前![]() 项之和
项之和![]() ,求证:
,求证:![]()
![]()
参考答案
一![]() 选择题
选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | D | B | D | A | B | A | B | B | B |
二![]() 填空题
填空题
11.{![]() } 12
} 12![]()
![]() 种
种 ![]() 13
13![]()
![]() 14
14![]() 120, 37
120, 37![]() 5
5
三![]() 解答题
解答题
15.(本小题满分12分)
解:(1)![]() 所以
所以![]()
![]() ………………………………3分
………………………………3分
所以当![]() 时,
时,![]() 为
为![]() ……………………………………6分
……………………………………6分
(2)由![]()
![]() 两边平方得
两边平方得![]() ,…………8分
,…………8分
即![]() ,
,
|
|
16.
解法一:(1) ![]() 时,
时,![]()
![]()
![]()
![]()

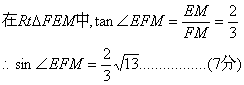

(2)设存实数![]() ,使
,使![]()
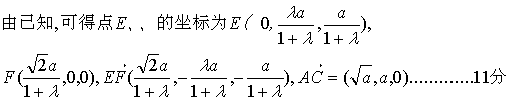
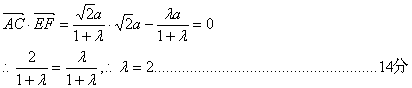
17![]() 设开关JA,JB ,JC ,JD 能够闭合的事件依次为A
设开关JA,JB ,JC ,JD 能够闭合的事件依次为A![]() B
B![]() C
C![]() D,则P(A)=P(D)=0
D,则P(A)=P(D)=0![]() 7,P(B)=P(C)=0
7,P(B)=P(C)=0![]() 8
8![]()
(1)P(B![]() C)=P(B)
C)=P(B)![]() P(c)=0
P(c)=0![]() 8╳0
8╳0![]() 8=0
8=0![]() 64…………………………5分
64…………………………5分![]()
(2)JA不能工作的概率为![]() JD不能工作的概率为
JD不能工作的概率为![]()
![]()
![]()
所以整条线路能正常工作的概率为0![]() 9676
9676
答:9月份这段线路能正常工作的概率为0![]() 9676
9676![]() …………………………14分
…………………………14分
18.解:(1)由题意知![]()

19.解:(1)![]() ,令
,令![]()
|
|
|
|
|
|
|
|
| + | 0 | - | 0 | + |
|
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
可见,当![]() 时,
时,
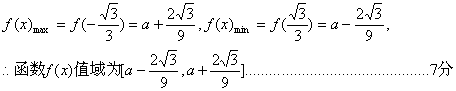
(2)如果对于任意![]() 即可证明
即可证明![]() 是“标准函数”;否则,
是“标准函数”;否则,![]() 不是“标准函数”
不是“标准函数”![]() …………………10分
…………………10分
![]()
![]() 所以
所以![]() 是“标准函数”
是“标准函数”![]() …………………14分
…………………14分![]()
20.![]()