广东省2006届高三年级五校联考
|
考试时间:120分钟 满分:150分
第Ⅰ卷(选择题 共50分)
一![]() 选择题(每小题5分,共10小题,共50分)
选择题(每小题5分,共10小题,共50分)![]() 把答案涂在答题卡上
把答案涂在答题卡上![]()
1.设![]() ,
,![]() ,则
,则![]() 是
是![]() 成立的
( )
成立的
( )
A.充分条件,但不是必要条件; B.必要条件,但不是充分条件;
C.充分且必要条件;
D.既不充分又不必要条件![]()
2.已知![]() ,
,![]() ,且
,且![]() 与
与![]() 平行,则
平行,则![]() ( )
( )
A.![]() ;
B.
;
B.![]() ;
C.
;
C.![]() ;
D.
;
D.![]()
![]()
3.函数![]() 是
( )
是
( )
A.周期为![]() 的奇函数;
B.周期为
的奇函数;
B.周期为![]() 的偶函数;
的偶函数;
C.周期为![]() 的奇函数;
D.周期为
的奇函数;
D.周期为![]() 的偶函数
的偶函数![]()
4.已知![]() ,则
,则![]() =
( )
=
( )
A.―1;
B.2;
C.![]() ;
D.―1或2
;
D.―1或2![]()
5.若![]() 是各项为正的等比数列,且公比
是各项为正的等比数列,且公比![]() ,则
,则![]() 与
与![]() 的大小关系是
( )
的大小关系是
( )
A.![]() ;
B.
;
B.![]() ;
;
C.![]() ;
D.不确定
;
D.不确定![]()
6.设全集![]() 是实数集
是实数集![]() ,
,![]() ,
,![]() ,则图中阴影部分所表示的集合是
( )
,则图中阴影部分所表示的集合是
( )
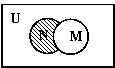 A.
A.![]() ;
B.
;
B.![]() ;
;
C.![]() ;
D.
;
D.![]()
![]()
7.若![]() ,则
,则![]() 的值等于
( )
的值等于
( )
A.![]() ;
B.
;
B.![]() ; C.
; C.![]() ;
D.
;
D.![]()
![]()
8.若![]() 是等差数列,
是等差数列,![]() 是其前
是其前![]() 项和,
项和,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,…,
,…,![]() 中最小的是
( )
中最小的是
( )
A.![]() ;
B.
;
B.![]() ; C.
; C.![]() ; D.
; D.![]()
![]()
9.设![]() 是定义在实数集
是定义在实数集![]() 上以2为周期的奇函数,已知
上以2为周期的奇函数,已知![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上
( )
上
( )
A.是减函数,且![]() ; B.是增函数,且
; B.是增函数,且![]() ;
;
C.是减函数,且![]() ; D.是增函数,且
; D.是增函数,且![]()
![]()
10.在△![]() 中,
中,![]() ,下列关系式中正确的是
( )
,下列关系式中正确的是
( )
A.![]() ;B.
;B.![]() ;
;
C.![]() ;D.
;D.![]()
![]()
2006 届 高 三 年 级 五 校 联 考
|
第Ⅱ卷(非选择题 共100分)
二.填空题:(本大题共4小题;每小题5分,共20分)
11.已知函数![]() ,则
,则![]()
![]()
12![]() 将函数
将函数![]() 的图象按向量
的图象按向量![]() (其中,
(其中,![]() )平移后与
)平移后与![]() 的图象重合,则向量坐标
的图象重合,则向量坐标![]() ,
,![]()
![]()
13.已知![]() 且
且![]() ,
,![]() ,当
,当![]() 时,均有
时,均有![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是
![]()
14.设函数![]()
![]() ,给出下列四个论断:
,给出下列四个论断:
①它的周期为![]() ;②在区间
;②在区间![]() 上是增函数;③它的图象关于点
上是增函数;③它的图象关于点![]() 成中心对称;④它的图象关于直线
成中心对称;④它的图象关于直线![]() 对称
对称![]()
请以其中两个论断为条件,另两个论断为结论,写出一个你认为正确的命题:
(请用如下形式答题:①②![]() ③④)
③④)![]()
三![]() 解答题:(共6小题,共80分)
解答题:(共6小题,共80分)
15.(本小题满分12分)若A![]() B
B![]() C是△ABC的内角,cosB=
C是△ABC的内角,cosB=![]() , sinC=
, sinC=![]() ,
,
求cosA的值![]()
16.(本小题满分12分)
已知数列![]() 满足:
满足: ![]() ,
,![]()
![]() 求证:数列
求证:数列![]() 是等比数列,并求其通项公式
是等比数列,并求其通项公式![]()
17![]() (本小题满分14分)已知函数:
(本小题满分14分)已知函数:![]()
![]()
(Ⅰ)求函数![]() 的最大值和最小值;
的最大值和最小值;
(Ⅱ)![]() 时,求函数
时,求函数![]() 满足
满足![]() 的x的集合
的x的集合![]()
18![]() (本小题满分14分)设函数
(本小题满分14分)设函数![]()
(Ⅰ)当![]() 求函数满足
求函数满足![]() 时的
时的![]() 的集合;
的集合;
(Ⅱ)求a的取值范围,使f(x)在区间(0,+∞)上是单调减函数![]()
19![]() (本小题满分14分)已知:f(x)=
(本小题满分14分)已知:f(x)=![]() ,数列{
,数列{![]() }的前n项和记为
}的前n项和记为![]() ,点
,点![]() (
(![]() ,
,![]() )在曲线y=f(x)上(n∈N+),且
)在曲线y=f(x)上(n∈N+),且![]() ,
, ![]()
![]()
(I)求数列{![]() }的通项公式;
}的通项公式;
(II)求证:![]()
![]()
(Ⅲ)数列{![]() }的前n项和为
}的前n项和为![]() ,且满足:
,且满足: ![]()
![]()
设定![]() 的值,使得数列{
的值,使得数列{![]() }是等差数列
}是等差数列![]()
20![]() (本小题满分14分)若定义在区间D上的函数
(本小题满分14分)若定义在区间D上的函数![]() 对于区间D上的任意两个值
对于区间D上的任意两个值![]() 总有以下不等式
总有以下不等式![]() 成立,则称函数
成立,则称函数![]() 为区间D上的凸函数;
为区间D上的凸函数;
(1)证明:定义在R上的二次函数![]() 是凸函数;
是凸函数;
(2)对于(1)中的二次函数![]() ,
,
若![]() ,求
,求![]() 取得最大值时函数
取得最大值时函数![]() 的解析式;
的解析式;
(3)定义在R上的任意凸函数![]() ,
,
若![]() ,证明:
,证明:![]()
![]()
广东省2006届高三五校联合考试
|
考试时间:120分钟 满分:150分
第Ⅰ卷(选择题 共60分)
一![]() 选择题(每小题5分,共10小题,共50分),把答案涂在答题卡上
选择题(每小题5分,共10小题,共50分),把答案涂在答题卡上![]()
1.( A )2.( C )3.( D )4.( B )5.( A )
6.( C )7.( B )8.( B )9.( D )10.( B )
第Ⅱ卷(非选择题 共100分)
二.填空题:(本大题共4小题;每小题5分,共20分)
11.
![]() 12
12![]()
![]()
![]() 1
1 ![]()
13. ![]()
![]() 14. ①④
14. ①④![]() ②③或 ①③
②③或 ①③![]() ②④
②④
三![]() 解答题:(共6小题,共74分)
解答题:(共6小题,共74分)
15.(本小题满分12分)若A![]() B
B![]() C是△ABC的内角,cosB=
C是△ABC的内角,cosB=![]() , sinC=
, sinC=![]() ,
,
求cosA的值![]()
解:∵ cosB=![]() , ∴sinB=
, ∴sinB=![]() , 又sinC=
, 又sinC=![]() , cosC=±
, cosC=±![]() , …………4分
, …………4分
若cosC=-![]() , 则角C是钝角,角B为锐角,π-C为锐角,而sin(π-C)=
, 则角C是钝角,角B为锐角,π-C为锐角,而sin(π-C)=![]() ,
,
sinB=![]() , 于是: sin(π-C)< sinB……(5分)
, 于是: sin(π-C)< sinB……(5分)
∴ B >π-C, B+C>π,矛盾,
∴ cosC≠-![]() , …………7分
, …………7分
cosC=![]() ,…………8分
,…………8分
![]()
故:cosA=-cos(B+C)=-(cosBcosC-sinBsinC)=![]() , …………12分
, …………12分
(说明:本题如果没有去掉cosC=![]() ,扣3分)
,扣3分)
16.(本小题满分12分)
已知数列![]() 满足:
满足: ![]() ,
,![]()
![]() 求证:数列
求证:数列![]() 是等比数列,并求其通项公式
是等比数列,并求其通项公式![]()
16![]() 解:
解:![]() 依题意得:
依题意得:
![]() …………2分
…………2分
![]()
![]() (n=1,2,…)…………5分
(n=1,2,…)…………5分
![]() …………8分
…………8分
故数列![]() 是等比数列
是等比数列![]() …………10分
…………10分
![]()
![]() …………12分
…………12分
17![]() (本小题满分14分)已知函数:
(本小题满分14分)已知函数:![]()
![]()
(Ⅰ)求函数![]() 的最大值和最小值;
的最大值和最小值;
(Ⅱ)当θ=![]() 时,求函数
时,求函数![]() 满足
满足![]() 的x的集合
的x的集合![]()
17. 解:(Ⅰ)![]() ] ………………2分
] ………………2分
![]() ……(4分)
……(4分)
= ![]() ……………6分
……………6分
![]() ………………8分
………………8分
(Ⅱ)由y =![]()
![]() ……………………12分
……………………12分
![]()
![]() …………14分
…………14分
18![]() (本小题满分14分)设函数
(本小题满分14分)设函数![]()
(Ⅰ)当![]() 求函数满足
求函数满足![]() 时的
时的![]() 的集合;
的集合;
(Ⅱ)求a的取值范围,使f(x)在区间(0,+∞)上是单调减函数![]()
18.解:(Ⅰ)当![]()
![]()
![]() ,化为
,化为![]() ……(3分)
……(3分)
![]()
![]()
故,满足(Ⅰ)条件的集合为![]()
![]() ……(5分)
……(5分)
(Ⅱ)在区间![]() 上任取
上任取![]() ,则
,则![]() ……(7分)
……(7分)![]() ……(8分)
……(8分)
因![]() 故
故![]() ,又在
,又在![]() 上
上![]() ,
,![]() ……(10分)
……(10分)
∴只有当![]() 时,即
时,即![]() 时
时![]()
才总有![]() , ……(12分)
, ……(12分)
∴当![]() 时,
时,![]() 在
在![]() 上是单调减函数
上是单调减函数![]() (14分)
(14分)
说明:本题若令![]() 求出
求出![]() ,没有考虑
,没有考虑![]() 的充分性扣2分
的充分性扣2分
19![]() (本小题满分14分)已知:f(x)=
(本小题满分14分)已知:f(x)=![]() ,数列{
,数列{![]() }的前n项和记为
}的前n项和记为![]() ,点
,点![]() (
(![]() ,
,![]() )在曲线y=f(x)上(n∈N+),且
)在曲线y=f(x)上(n∈N+),且![]() ,
, ![]()
![]()
(I)求数列{![]() }的通项公式;
}的通项公式;
(II)求证:![]()
![]()
(Ⅲ)数列{![]() }的前n项和为
}的前n项和为![]() ,且满足:
,且满足: ![]()
![]()
设定![]() 的值,使得数列{
的值,使得数列{![]() }是等差数列
}是等差数列![]()
19![]() 解:(Ⅰ)由于y=
解:(Ⅰ)由于y=![]()
∵点An(![]() ,
,![]() )在曲线y=f(x)上(n∈N+)
)在曲线y=f(x)上(n∈N+)
∴![]() = f(
= f(![]() )=
)= 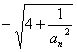 , 并且
, 并且![]() ……(2分)
……(2分)
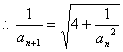 ,
, ![]()
∴数列{![]() }为等差数列,并且首项为
}为等差数列,并且首项为![]() =1,公差为4 ……(4分)
=1,公差为4 ……(4分)
∴![]() =1+4(n—1) ,
∴
=1+4(n—1) ,
∴![]()
∵ ![]() ,
,
∴![]() ……(5分)
……(5分)
(II)![]()
![]() ……(8分)
……(8分)
![]() ……(10分)
……(10分)
(Ⅲ)由![]() ,
, ![]()
得:![]()
![]() ……(12分)
……(12分)
![]()
![]() ,如果
,如果![]() ,此时
,此时![]()
![]() ……(13分)
……(13分)
![]()
![]() ,
,
此时,数列{![]() }是等差数列
}是等差数列![]() ……(14分)
……(14分)
20![]() (本小题满分14分)若定义在区间D上的函数
(本小题满分14分)若定义在区间D上的函数![]() 对于区间D上的任意两个值
对于区间D上的任意两个值![]() 总有以下不等式
总有以下不等式![]() 成立,则称函数
成立,则称函数![]() 为区间D上的凸函数 ;
为区间D上的凸函数 ;
(1)证明:定义在R上的二次函数![]() 是凸函数;
是凸函数;
(2)对于(1)中的二次函数![]() ,
,
若![]() ,求
,求![]() 取得最大值时函数
取得最大值时函数![]() 的解析式;
的解析式;
(3)定义在R上的任意凸函数![]() ,
,
若![]() ,证明:
,证明:![]()
![]()
20![]() 证明:(1)任取x1
证明:(1)任取x1![]() x2
x2![]() R,则
R,则
2f(![]() )-[f(x1)+f(x2)]
)-[f(x1)+f(x2)]
=2[a(![]() )2 + b
)2 + b![]() +c] -[a x12+bx1+c] - [a x22+bx2+c]
+c] -[a x12+bx1+c] - [a x22+bx2+c]
=![]() [(x1+x2)2-2(x12+x22)]=
-
[(x1+x2)2-2(x12+x22)]=
-![]() (x1-x2)2
……(2分)
(x1-x2)2
……(2分)
![]() a<0
a<0
![]() 2f(
2f(![]() )-[f(x1)+f(x2)]
)-[f(x1)+f(x2)] ![]() 0
0
![]()
![]()
![]() 由定义得 y = f(x)是R上的凸函数 ……(4分)
由定义得 y = f(x)是R上的凸函数 ……(4分)
(2)![]()
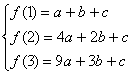 解得
解得 ……(5分)
……(5分)
![]() f(4)=16a+4b+c=f(1)-3f(2)+3f(3)
f(4)=16a+4b+c=f(1)-3f(2)+3f(3)![]() f(1)+3f(2)+3f(3)
f(1)+3f(2)+3f(3)
![]() f(1)
f(1) ![]() 1,f(2)
1,f(2) ![]() 2,f(3)
2,f(3) ![]() 3
3
![]() f(4)
f(4) ![]() f(1)+3f(2)+3f(3)
f(1)+3f(2)+3f(3) ![]() 16 ……(6分)
16 ……(6分)
![]() a<0时f(x)= ax2+bx+c开口向下,
a<0时f(x)= ax2+bx+c开口向下,
![]() 当且仅当
当且仅当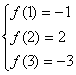 时取等号,代入上式得
时取等号,代入上式得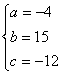
![]() f(x)= -4x2+15x-12
……(8分)
f(x)= -4x2+15x-12
……(8分)
(3)![]() p
p![]() q
q![]() m
m![]() n
n![]() 且p<m<n<q
且p<m<n<q
不妨设m = p+i, 其中i![]()
![]() p+q = m+n
p+q = m+n
![]() m-p = q-n = i
m-p = q-n = i
由定义知,任意x1![]() x2
x2![]() R,有f(x1)+f(x2)
R,有f(x1)+f(x2)![]() 2f(
2f(![]() ) ……(9分)
) ……(9分)
取x1 =
p![]() x2 = p+2则有f(p)+f(p+2)
x2 = p+2则有f(p)+f(p+2) ![]() 2f(p+1)
2f(p+1)
变形得f(p) -f(p+1) ![]() f(p+1) - f(p+2)
f(p+1) - f(p+2)
同理有 f(p+1) -f(p+2) ![]() f(p+2) - f(p+3)
f(p+2) - f(p+3)
f(p+2) -f(p+3) ![]() f(p+3) -f(p+4)
f(p+3) -f(p+4)
f(p+4) -f(p+5) ![]() f(p+5) - f(p+6)
f(p+5) - f(p+6)
… …
f(p+k-2) - f(p+k-1) ![]() f(p+k-1) -f(p+k)
f(p+k-1) -f(p+k)
累加求和得:f(p)-f(p+k-1) ![]() f(p+1) -f(p+k)
f(p+1) -f(p+k)
即 f(p)+ f(p+k) ![]() f(p+1)+ f(p+k-1) ……(11分)
f(p+1)+ f(p+k-1) ……(11分)
递推i次得
f(p)+ f(p+k) ![]() f(p+1)+ f(p+k-1)
f(p+1)+ f(p+k-1) ![]() f(p+2)+f(p+k-2)
f(p+2)+f(p+k-2) ![]() …
…![]() f(p+i)+f(p+k-i)
f(p+i)+f(p+k-i)
![]() f(p)+ f(p+k)
f(p)+ f(p+k)![]() f(p+i)+f(p+k-i)
f(p+i)+f(p+k-i)
令p+k = q,得f(p)+f(q) ![]() f(p+i) + f(q-i)
f(p+i) + f(q-i)
![]() m-p = q-n = i
m-p = q-n = i
![]() f(p)+f(q)
f(p)+f(q) ![]() f(m)+f(n)
……(14分)
f(m)+f(n)
……(14分)