2005-2006学年度九江中学高三数学检测2005
10
单选题(每道小题 5分 共 60分 )
1 下列不等式中，解集是空集的是 [
]
A．│x+2│>=0 B．x2+6x+9<=0
C，x2+3x-1<=0 D．x2-x+1<=0
2
3 若y = f ( x ) 的定义域是[0，1]，则 f ( x + a ) + f (2 x + a) ( 0 a 1)的定域 [
]
4 如果全集Ｉ＝{a,b,c,d,e}，M＝{a,c,d},N={b,d,e},那么，
[
]
A、
B、{d} C、{a,b} D、{b,e}
5 如果a、b是异面直线，下列判断中一定正确的是 [
]
A．过b的平面中，没有与a平行的
B．过b的平面中，有且只有一个与a平行
C．过b的平面中，没有与a垂直的
D．过b的平面中，有且只有一个垂直于a
6 把正方形ABCD沿对角线AC折起，当A、B C、D四点为顶点的三棱锥体积最大时，直线BD与平面ABC所成的角的大小为 （ ）
A．90° B．60° C．45° D．30°
7
8 椭圆
上的点到直线
的最大距离是[
]
（A）3（B）
（C）
（D）
9 从－3，－2，－1，1，2，3中任取三个不同的数作为椭圆方程
中的系数，则确定不同椭圆的个数为
（ ）
A．20 B．18 C．9 D． 16
10 设M、O、A、B、C是空间的点，则使M、A、B、C一定共面的等式是[ ]
A．
B．
C．
D．
11 从10名女学生中选2名，40名男生中选3名，担任五种不同的职务，规定女生不担任其中某种职务，不同的分配方案有
[ ]
A．P102P403 B．C102P31P44C103 C．C152C403P55 D．C102C403
12 设f(x)是定义在实数集上的函数，且满足下列关系f(10+x)=f(10-x),f(20-x)=-f(20+x),则f(x)是[ ]
(A)偶函数，又是周期函数
(B)偶函数，但不是周期函数
(C)奇函数，又是周期函数
(D)奇函数，但不是周期函数
二 填空题(每道小题6分 共30分)
13 函数
的值域为
14 等差数列{An}的前m项的和为30,前2m项的和为100,求它的前3m项的和______________
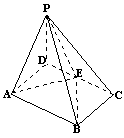
15 如图，在四棱锥P－ABCD中，E为CD上的动点，四边形ABCD为
时，体积VP－AEB恒为定值（写上你认为正确的一个答案即可）．
16 已知函数
给出下列命题：①f(x)必是偶函数；②f(0)=
f(2)时，f(x)的图象必关于直线x=1对称；③若
，则f(x)在区间
上是增函数；
④f(x)有最小值
其中正确命题的序号是
17 正三角形边长为1,且向量BC=a,CA=b,AB=c,求a+b+c=__________
三 解答题(18题10分,19题11分,20题12分,21题13分,22题14分)
18 
19 已知不等式
对于大于1的正整数n恒成立，试确定a的取值范围
20 在△ABC中，a，b，c分别是角A，B，C的对边，且8sin2
(I)求角A的大小；
(II) 若a=
，b+c=3，求b和c的值
21 如图，直三棱柱ABC-A1B1C1，底面△ABC中，CA=CB=1，∠BCA=90º，
棱AA1=2，M、N分别是A1B1，A1A的中点，
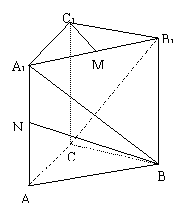（I）求
的长；
（II）求cos<
,
>的值；
（III）求证：A1B⊥C1M （9分）
22 设曲线
在点
处的切线斜率为
，且
,对一切实数，不等式
恒成立（
）
（1）求
的值；
（2）求函数的表达式；
（3）求证：
试题答案 2005 10
选择题
1 D 2 B 3 A 4 B 5 A 6 C 7 B 8 D 9 B 10 B 11 B 12 C
二 填空题
13 
14 210 15 AB∥CD 16 ③ 17 6½
三 解答题
18
19 构造函数
，易证
为增函数
∵n是大于1的 正整数，
对一切大于1的正整数恒成立，必须
,
即
20 （I）在△ABC中有B+C=π－A，由条件可得：
4[1－cos(B+C)] －4cos2A+2=7
又∵cos(B+C)= －cosA
∴4cos2A－4cosA+1=0
解得
解： （II）由
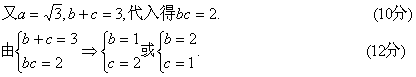
21 ；
；略；
22 ⑴解：
，
, 
, 
(2)解：
, 
，
又
即
(3)证明:
，原式
…
…
…
…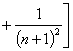