2005—2006学年度上学期高三年级第四次月考
数 学 试 卷 2005年12月
本试卷第Ⅰ、Ⅱ卷1~4页,答题卷5~8页,试卷满分150分。考试时间120分钟。
注意事项:
1.答题前,考生务必将自己的学校、姓名、号码、班级填写在答题卷指定位置。
2.第Ⅰ、Ⅱ卷答案写在答题卷指定答题处,不得超出答题范围。
第Ⅰ卷(选择题,共60分)
一、选择题:(本大题共10个小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是最符合题目要求的,请将所选答案填在第Ⅱ卷指定的答题栏内)
1.函数![]() 的最小正周期是( )
的最小正周期是( )
![]()
![]()
![]()
![]()
2.若![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
![]()
![]()
![]()
![]()
3.已知等差数列的前n项和为Sn,若![]() ,则S8等于( )
,则S8等于( )
A.18 B.36 C.54 D.72
4.条件![]() ┓p是 ┓q的( )
┓p是 ┓q的( )
A.充分条件但不是必要条件 B.必要条件但不是充分条件
C.充要条件 D.既不是充分条件又不是必要条件
5.设![]() ,当
,当![]() ,且
,且![]() 时,点C在 ( )
时,点C在 ( )
A. 直线A B上 B.线段AB上
C. 直线AB上,但除去点A D.直线AB上,但除去点B
6.已知![]() ≤
≤![]() ≤
≤![]() ,向量
,向量![]() ,则
,则![]() 的 ( )
的 ( )
A.最大值是1,最小值是-1 B.最大值是1,最小值是![]()
C.最大值是2,最小值是-2 D.最大值是2,最小值是-1
7.过已知圆内的一个定点作圆C与已知圆相切,则圆C的圆心轨迹是( )。
A 圆 B 椭圆 C 圆或椭圆 D 线段
8. 函数![]()
![]() 的图象的大致形状是 ( )
的图象的大致形状是 ( )
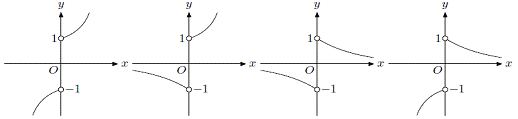
A. B. C. D.
9.已知数列![]() 满足
满足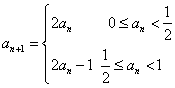 ,若
,若![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.经济学中的“蛛网理论”(如图),假定某种商品的“需求—价格”函数的图象为直线l1,“供给—价格”函数的图象为直线l2,它们的斜率分别为k1、k2,l1与l2的交点P为“供给—需求”均衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点P,与直线l1、 l2的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点P的条件为 ( )
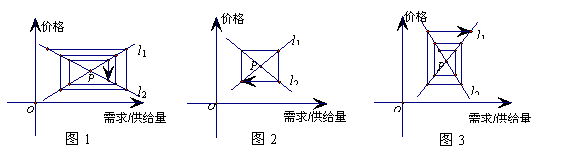 |
A.k1+k2>0 B.k1+k2=0 C.k1+k2<0 D.k1+k2可取任意实数
二、填空题:((本大题共5个小题,每小题4分,共20分,把正确答案填在题中所给横线上。)
11.已知双曲线的渐近线方程是y=±x,焦点在坐标轴上,焦距是10,则它的方程为
。
12.在算式“4×□+1×□=6”的两个□中,分别填入两个自然数,使它们的倒数之和最小,则这两个数应分别为 。
13.设双曲线![]() 的右准线与两渐近线相交于A、B两点,F为右焦点,以AB为直径的圆恰过点F,则双曲线的离心率为 ;
的右准线与两渐近线相交于A、B两点,F为右焦点,以AB为直径的圆恰过点F,则双曲线的离心率为 ;
14.不等式组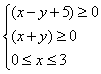 ,表示的平面区域的面积是
;
,表示的平面区域的面积是
;
 15.函数
15.函数![]() ,它的最小正周期为
,它的最小正周期为![]() ,且其图像关于直线
,且其图像关于直线![]() 对称,则在下面四个结论中:①图像关于点(
对称,则在下面四个结论中:①图像关于点(![]() 对称;②图像关于点
对称;②图像关于点![]() 对称;③它可以由函数
对称;③它可以由函数![]() 图象上所有点向左平移
图象上所有点向左平移![]() 个单位,横坐标不变,纵坐标向下平移1个单位而得到;④在[
个单位,横坐标不变,纵坐标向下平移1个单位而得到;④在[![]() 上是增函数.所有正确结论的序号为
.
上是增函数.所有正确结论的序号为
.
第Ⅱ卷(选择题,共80分)
三、解答题:(共6小题,80分. 解答须写出必要的文字说明、证明过程及演算步骤)
16.已知![]() 、
、![]() 、
、![]() 三点的坐标分别为
三点的坐标分别为![]() 、
、![]() 、
、![]() ,
,![]() ,
,
(I)若![]() ,求角
,求角![]() 的值;
的值;
(II)若![]() ,求
,求![]() 的值。(12分)
的值。(12分)
17.已知数列{an}的前n项和为Sn,且an+Sn=1(n∈N*)。
⑴求数列{an}的通项公式;
⑵若数列{bn}满足![]() ,求
,求![]() 的值。(12分)
的值。(12分)
18.已知定义域为[0,1]的函数![]() 同时满足:(1)对于任意
同时满足:(1)对于任意![]()
(2)![]() (3)若
(3)若![]()
(Ⅰ)试求![]() 的值; (Ⅱ)试求函数
的值; (Ⅱ)试求函数![]() 的最大值; (Ⅲ)若对于任意
的最大值; (Ⅲ)若对于任意![]() 总有
总有![]() ,求实数
,求实数![]() 的取值范围。(14分)
的取值范围。(14分)
19.某地区发生流行性病毒感染,居住在该地区的居民必须服用一种药片预防,规定每人每天上午![]() 时和晚上
时和晚上![]() 时各服一片。现知该药片每片含药量为
时各服一片。现知该药片每片含药量为![]() 毫克,若人的肾脏每
毫克,若人的肾脏每![]() 小时从体内滤出这种药的
小时从体内滤出这种药的![]() ,该药物在人体内的残留量超过
,该药物在人体内的残留量超过![]() 毫克,就将产生副作用。
毫克,就将产生副作用。
(Ⅰ)某人上午![]() 时第一次服药,问到第二天上午
时第一次服药,问到第二天上午![]() 时服完药后,这种药在他体内还残留多少?
时服完药后,这种药在他体内还残留多少?
(Ⅱ)若人长期服用这种药,这种药会不会对人体产生副作用?说明理由。(12分)
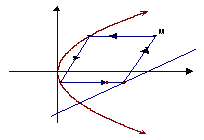 20.抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,如右图所示,今有抛物线
20.抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,如右图所示,今有抛物线![]() ,一光源在点
,一光源在点![]() 处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线
处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线![]() 上的点N,再反射后又射回点M。
上的点N,再反射后又射回点M。
(1)设P、Q两点的坐标分别是![]() ,
,
证明:![]() 。
。
(2)求抛物线方程。(14分)
21.以O为原点,![]() 所在直线为
所在直线为![]() 轴,建立如 所示的坐标系。设
轴,建立如 所示的坐标系。设![]() ,点F的坐标为
,点F的坐标为![]() ,
,![]() ,点G的坐标为
,点G的坐标为![]() 。
。
(1)求![]() 关于
关于![]() 的函数
的函数![]() 的表达式,判断函数
的表达式,判断函数![]() 的单调性,并证明你的判断;
的单调性,并证明你的判断;
(2)设ΔOFG的面积![]() ,若以O为中心,F为焦点的椭圆经过点G,求当
,若以O为中心,F为焦点的椭圆经过点G,求当![]() 取最小值时椭圆的方程;
取最小值时椭圆的方程;
(3)在(2)的条件下,若点P的坐标为![]() ,C、D是椭圆上的两点,且
,C、D是椭圆上的两点,且![]() ,求实数
,求实数![]() 的取值范围。(16分)
的取值范围。(16分)
2005—2006学年度上学期高三年级第四次月考
数 学 答 案
BDDAA DCDBA
11.![]() 12.1,2 13.
12.1,2 13.![]() 14.24 15. ③④
14.24 15. ③④
16.解:(1)![]()
![]() ,
,
![]() (………………………3分)
(………………………3分)
由![]() 得
得![]()
又![]()
![]() (…………6分)
(…………6分)
(2)由![]() ,得
,得![]()
![]()
![]() (…………………9分)
(…………………9分)
又![]() =
=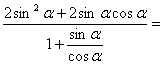
![]()
所以,![]() =
=![]() 。
(………………12分)
。
(………………12分)
17.解:⑴由an+Sn=1,∴an+1+Sn+1=1,两式相减,∴an+1-an+Sn+1-Sn=0,∴2an+1=an,∴数列{an}是公比为的等比数列。………………………………………3分
又n=1时,a1+S1=1,∴a1=,∴an=a1qn-1=·()n-1=()n。…………………6分
⑵∵![]() ,当
,当![]() 时,
时,![]()
当![]() ,
,![]()
则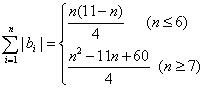 12分
12分
18.解:(Ⅰ)对于条件③,令![]()
又由条件①知![]() 故
故![]() (4分)
(4分)
(Ⅱ)设![]() ,则
,则![]()
![]()
即![]() 故
故![]() 在[0,1]上是单调递增的
在[0,1]上是单调递增的
从而![]() 的最大值是
的最大值是![]() (8分)
(8分)
(Ⅲ)因![]() 在
在![]() 上是增函数,则
上是增函数,则![]() ,
,
又(![]() 对
对![]() 恒成立,
恒成立,
设![]()
则![]() (14分)
(14分)
19.解:(Ⅰ)设人第![]() 次服药后,药在体内的残留量为
次服药后,药在体内的残留量为![]() 毫克,则
毫克,则
![]() ,
,![]() ,
,
![]() ,即到第二天上午时服完药后,这种药在他体内还残留
,即到第二天上午时服完药后,这种药在他体内还残留![]() 毫克; (6分)
毫克; (6分)
(Ⅱ)由题意:![]() ,∴
,∴![]() ,
,
∴![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,
为公比的等比数列,
∴![]() ,(10分)
,(10分)
∵![]() ,∴
,∴![]() ,∴
,∴![]() 。故若人长期服用这种药,这种药不会对人体产生副作用。(14分)
。故若人长期服用这种药,这种药不会对人体产生副作用。(14分)
20.解(1)由抛物线的光学性质及题意知光线PQ必过抛物线的焦点![]() ,设
,设![]() ,代入抛物线方程得:
,代入抛物线方程得:![]() ,
,![]() (6分)
(6分)
(2)设![]() ,由题意知
,由题意知![]() ,又设
,又设![]() 是点M关于直线l的对称点,则有:
是点M关于直线l的对称点,则有: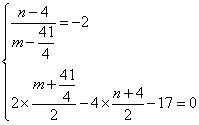 ,
,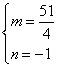 ,
,
由对称性质知![]() ,代入直线l的方程得
,代入直线l的方程得![]() (或利用到角公式得
(或利用到角公式得![]() ,求出
,求出![]() )。由
)。由![]() ,则
,则![]() ,又P,F,Q三点共线得P=2。抛物线方程为
,又P,F,Q三点共线得P=2。抛物线方程为![]() 。(14分)
。(14分)
21.解(1)由题意知![]() ,则
,则![]()
函数![]() 在
在![]() 是单调递增函数。(证明略)(5分)
是单调递增函数。(证明略)(5分)
(2)由![]() ,点G
,点G![]() ,
,
因![]() 在
在![]() 上是增函数,当
上是增函数,当![]() 时,
时,![]() 取最小值,此时
取最小值,此时![]() ,
,
依题意椭圆的中心在原点,一个焦点F(3,0),设椭圆方程为![]() ,由G点坐标代入与焦点F(3,0),可得椭圆方程为:
,由G点坐标代入与焦点F(3,0),可得椭圆方程为:![]() (10分)
(10分)
(3)设![]() ,则
,则![]() ,
,
由![]() ,
,![]() ,
,
因点C、D在椭圆上,代入椭圆方程得,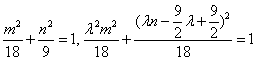 ,消去
,消去![]() ,
,
得![]() ,又
,又![]() ,
,
则实数![]() 的取值范围为
的取值范围为![]() 。(16分)
。(16分)