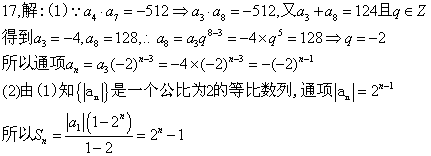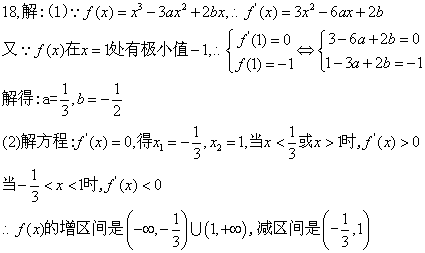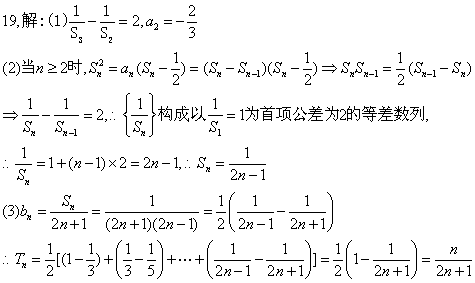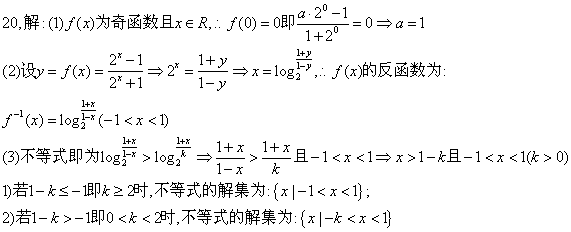南安二中2006届高三数学十月份月考试题
第I卷(理)
(时间:120分钟 分值:150分)
一 ![]() 选择题:本题共有12个小题,每小题5分,共60分
选择题:本题共有12个小题,每小题5分,共60分
![]()
1.![]() ( )
( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.![]() ( )
( )
A.36 B.18 C.72 D.9
3.![]()
![]() ( )
( )
A ![]()
![]() B
B ![]()
![]() C
C ![]()
![]() D
D ![]()
![]()
4.设函数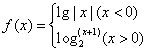 ,若
,若![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.若等比数列![]() 的公比为q,则“
的公比为q,则“![]() ”是“对于任意正整数n,都有
”是“对于任意正整数n,都有![]() 的( )
的( )
A.充分非必要条件B.必要非充分条件C.充要条件 D.即非充分也必要条件
7.函数![]() 与
与![]() 的图象关于
的图象关于![]() 对称,则
对称,则![]() 的单调递增区间为( )
的单调递增区间为( )
(A) ![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D)![]()
8.已知数列前n项和![]() ,则此数列的奇数项的前n项的和是( )
,则此数列的奇数项的前n项的和是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.函数![]() 的定义域分成四个单调区间的充要条件是( )
的定义域分成四个单调区间的充要条件是( )
A.![]() B
B ![]()
![]() C
C ![]()
![]() D
D ![]()
![]()
10.设![]() ,则集合
,则集合![]() 中元素个数是 (
)
中元素个数是 (
)
(A ) 无穷多个 (B) 2 (C) 3 (D) 4
11.等比数列![]() 记
记![]() ,如果
,如果![]() ( )
( )
A.14 B.18 C.144 D.-102
12.设![]() 且
且![]() :
:
①![]() ②
②![]() ③
③![]()
④![]() ,其中所有正确命题的序号是
,其中所有正确命题的序号是
(A)①② (B) ②④ C)①②④ (D) ②③④
第II卷(非选择题,共90分)
二 ![]() 填空题:本大题共4小题,每小题4分,共16分,把答案填在题中的横线上
填空题:本大题共4小题,每小题4分,共16分,把答案填在题中的横线上
![]()
13.已知![]() ,则不等式
,则不等式![]() 的解集为
的解集为
![]()
14.已知![]() 为等比数列,
为等比数列,![]() ,则
,则![]()
![]()
15.若函数![]() 的图象关于直线x=0对称,则b=
的图象关于直线x=0对称,则b= ![]()
16.数列![]() 中,
中,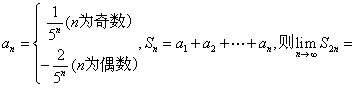
![]()
三 ![]() 解答题:本大题共6小题,共74分,解答应写出文字说明
解答题:本大题共6小题,共74分,解答应写出文字说明 ![]() 证明过程或推演步骤
证明过程或推演步骤
![]()
17.等比数列![]() 中,
中,![]() ,
,![]()
(1)求![]()
(2)![]()
![]()
18.已知函数![]() 在x = 1 处有极小值-1
在x = 1 处有极小值-1 ![]()
①求a,b的值
②求出函数![]() 的单调区间
的单调区间 ![]()
19 ![]() 数列
数列![]() 中,
中,![]() 时,其前n项和
时,其前n项和![]() 满足
满足![]()
①求![]() 的值
的值
②证明![]() 是等差数列,并求
是等差数列,并求![]() 的表达式
的表达式 ![]()
③设![]() ,求数列
,求数列![]()
![]()
20 ![]() 已知
已知![]() 是定义在R上的函数且其函数图象关于原点对称
是定义在R上的函数且其函数图象关于原点对称 ![]()
①求a的值 ![]()
②求![]() 的反函数
的反函数![]() 的解析式
的解析式 ![]()
③对于任意的![]() ,解不等式
,解不等式![]()
21 ![]() 学校餐厅每天供应1000名学生用餐,每星期一有A
学校餐厅每天供应1000名学生用餐,每星期一有A ![]() B两样菜可供选择,调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B菜,而选B菜的,下周星期一则有30%改选A菜,若用
B两样菜可供选择,调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B菜,而选B菜的,下周星期一则有30%改选A菜,若用![]() 分别表示在第n个星期一选A
分别表示在第n个星期一选A ![]() B菜的人数
B菜的人数
![]()
①试以![]() 表示
表示![]() ;
;
②若![]() ,求
,求![]() 的通项公式;
的通项公式;
③问第n个星期一时,选A菜与选B菜的人数相等?
22 ![]() 已知函数
已知函数![]() 在
在![]() 上最小值是
上最小值是![]()
①求函数![]() 的导数
的导数![]() 及
及![]() 在
在![]() 上单调区间;
上单调区间;
②求数列![]() 的通项公式;
的通项公式;
③证明:![]()
④在点列![]() 中是否存在两点
中是否存在两点![]() ,使直线
,使直线![]() 的斜率为1?若存在,求出所有的数对
的斜率为1?若存在,求出所有的数对![]() ;若不存在,请说明理由
;若不存在,请说明理由 ![]()
南安二中2006届高三年级十月份月考试题
数学(理)参考答案
一 ![]() 选择题:(每题5分共60分)
选择题:(每题5分共60分)
1 ![]() B 2
B 2 ![]() A 3
A 3 ![]() B 4
B 4 ![]() D 5
D 5 ![]() D 6
D 6 ![]() A 7
A 7 ![]() C 8
C 8 ![]() C 9
C 9 ![]() B 10
B 10 ![]() C 11
C 11 ![]() A 12
A 12 ![]() C
C
二 ![]() 填空题:(每题4分共16分)
填空题:(每题4分共16分)
13.![]() 14.1 15.2 16.
14.1 15.2 16.![]()
三 ![]() 解答题:(共6大题,其中第17-----21题每题12分,第22题14分,共74分)
解答题:(共6大题,其中第17-----21题每题12分,第22题14分,共74分)