绝密★启用前
2005年10月济南市高三统一考试
数 学(理工类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分![]() 第Ⅰ卷1至2页,第Ⅱ卷3至8页
第Ⅰ卷1至2页,第Ⅱ卷3至8页![]() 共150分
共150分![]() 测试时间120分钟
测试时间120分钟![]()
第Ⅰ卷(选择题 共60分)
注意事项:
1. 第Ⅰ卷前,考生务必将自己的姓名![]() 准考证号
准考证号![]() 考试科目用铅笔涂写在答题卡上
考试科目用铅笔涂写在答题卡上![]()
2. 选择题为四选一题目,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑![]() 如需改动,用橡皮擦干净后,再选涂其它答案
如需改动,用橡皮擦干净后,再选涂其它答案![]() 不能答在测试卷上
不能答在测试卷上![]()
一、选择题:本大题共12小题![]() 每小题5分;共60分
每小题5分;共60分![]() 在每小题给出的四个选项中,只有
在每小题给出的四个选项中,只有
一项是符合题目要求的![]()
⒈已知复数![]() ,则复数
,则复数![]()
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
⒉设![]() 与
与![]() 是两个不共线向量,且向量
是两个不共线向量,且向量![]() 与
与![]() 共线,则
共线,则![]() =
=
A![]() 0 B
0 B![]() -1
C
-1
C![]() -2 D
-2 D![]() -0
-0![]() 5
5
⒊已知全集![]() ,集合
,集合![]() ,则满足条件的
,则满足条件的
集合![]() 共有
共有
A![]() 4个 B
4个 B![]() 6个 C
6个 C![]() 8个 D
8个 D![]() 16个
16个
⒋若![]() 则下列结论不正确的是
则下列结论不正确的是
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
⒌已知函数![]() 的反函数为
的反函数为![]()
![]() ,且
,且![]()
![]() 的图像经过第三
的图像经过第三![]() 四象限,那么函数
四象限,那么函数![]() -
-![]() 的图像必经过的象限是
的图像必经过的象限是
A![]() 第一
第一![]() 二象限 B
二象限 B![]() 第二
第二![]() 三象限 C
三象限 C![]() 第一
第一![]() 三象限 D
三象限 D![]() 第二
第二![]() 四象限
四象限
⒍直线![]() 在两坐标轴上的截距都大于0,则直线的倾斜角为
在两坐标轴上的截距都大于0,则直线的倾斜角为
A![]()
![]() B
B![]() -
-![]() C
C![]() π-
π-![]() D
D![]() π+
π+![]() π
π
高三(理工类)数学试题第1页(共6页)
⒎函数![]() 的图像按向量
的图像按向量![]() 平移后,所得函数的解析式是
平移后,所得函数的解析式是![]() ,则
,则![]() 等于
等于
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
⒏下列函数在![]() 连续的是
连续的是
A![]()
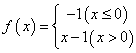 B
B![]()
![]()
C![]()
![]() D
D![]()
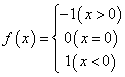
⒐下列命题中不正确的是(其中![]() 表示直线,
表示直线,![]() 表示平面)
表示平面)
A![]()
![]() B
B![]()
![]()
C![]()
![]() D
D![]()
![]()
⒑某文艺团体下基层进行宣传演出,原准备的节目表中有6个节目,如果保持这些节目的
相对顺序不变,在它们之间再插入2个小品节目,并且这2个小品节目在节目表中既不
排头,也不排尾,则不同的插入方法有
A![]() 20种 B
20种 B![]() 30种 C
30种 C![]() 42种 D
42种 D![]() 56种
56种
⒒若![]() 的展开式中各项二项式系数之和为
的展开式中各项二项式系数之和为![]() ,
,![]() 的展开式中各项系数之和为
的展开式中各项系数之和为![]() ,则
,则![]() 的值为
的值为
A![]()
![]() B
B![]() -
-![]() C
C![]()
![]() D
D![]() -
-![]()
⒓已知点![]() 为椭圆
为椭圆![]() 上的点,
上的点,![]()
![]()
![]() 是椭圆的左
是椭圆的左![]() 右焦点,
右焦点,![]() 在线段
在线段![]() 上,且
上,且![]() ,那么点
,那么点![]() 分有向线段
分有向线段![]() 的比是
的比是
A![]() 3:4 B
3:4 B![]() 4:3 C
4:3 C![]() 2:5 D
2:5 D![]() 5:2
5:2
绝密★启用前
2005年10月济南市高三统一考试
数 学(理工类)
第Ⅱ卷(非选择题 共90分)
注意事项:
⒈第Ⅱ卷共6页,用钢笔或圆珠笔直接写在试题卷中![]()
⒉答卷前将密封线内的项目填写清楚![]()
| 得分 | 评卷人 |
二、填空题:本大题共4个小题![]() 每小题4分;共16分,把答案填在题中横线上
每小题4分;共16分,把答案填在题中横线上![]()
|
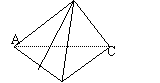 ⒕在正三棱锥
⒕在正三棱锥![]() 中,
中,![]() 为
为![]() 中点,且
中点,且
![]() 与
与![]() 所成角为
所成角为![]() ,则
,则![]() 与底面
与底面![]()
|
|
⒖已知椭圆![]() ,以原点为顶点,椭圆焦点
,以原点为顶点,椭圆焦点![]() 为焦点的抛物线
为焦点的抛物线
与椭圆相交与点![]() 且
且![]() 轴,则椭圆的离心率为
轴,则椭圆的离心率为
![]()
⒗下列结论中是真命题的有
(填上所有命题的序号)![]()
①“![]() ”是“
”是“![]() ”的必要不充分条件;②向量
”的必要不充分条件;②向量![]() 与向量
与向量![]() 共
共
线,向量![]() 与向量
与向量![]() 共线,则向量
共线,则向量![]() 与向量
与向量![]() 共线;③函数
共线;③函数![]() 是
是
奇函数;④函数![]() 与函数
与函数![]() 互为反函数
互为反函数![]()
三、解答题:本大题共6小题,共74分![]() 解答应写出文字说明,证明过程或演算步骤
解答应写出文字说明,证明过程或演算步骤![]()
| 得分 | 评卷人 |
17.(本小题满分12分)
已知![]()
![]() 求:
求:
⑴![]() ;
;
⑵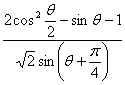
![]()
| 得分 | 评卷人 |
18.(本小题满分12分)
有红蓝两粒质地均匀的正方体形状骰子,红色骰子有两个面是8,四个面是2,蓝色骰子有三个面是7,三个面是1,两人各取一只骰子分别随机投掷一次,所得点数较大者获胜![]()
⑴分别求出两只骰子投掷所得点数的分布列及期望;
⑵投掷蓝色骰子者获胜的概率是多少?
| 得分 | 评卷人 |
19.(本小题满分12分)
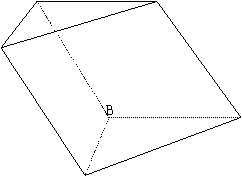
|
|
|
⑵求直线![]() 与平面
与平面![]() 所成角的正切
所成角的正切![]()
|
|
| 得分 | 评卷人 |
20.(本小题满分12分)
已知函数![]()
![]()
⑴若函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,求实数
上单调递增,求实数![]() 的值;
的值;
⑵求证:当![]() 时,
时,![]() 在
在![]() 上单调递减
上单调递减![]()
| 得分 | 评卷人 |
21.(本小题满分12分)
已知数列![]()
![]()
![]() 满足
满足![]() (
(![]() 为常数且
为常数且![]() ≠0),且
≠0),且![]()
![]()
⑴判断数列![]() 是否为等差数列,并证明你的结论;
是否为等差数列,并证明你的结论;
⑵若![]() ,作数列
,作数列![]() ,使
,使![]() ,
,
求和:![]()
![]()
| 得分 | 评卷人 |
22.(本小题满分14分)
椭圆![]() 的左
的左![]() 右焦点分别为
右焦点分别为![]()
![]()
![]() ,右顶点为
,右顶点为![]() 为椭圆
为椭圆![]() 上任意一点,且
上任意一点,且![]() 最大值的取值范围是
最大值的取值范围是![]() ,其中
,其中![]()
![]()
⑴求椭圆![]() 的离心率
的离心率![]() 的取值范围;
的取值范围;
⑵设双曲线![]() 以椭圆
以椭圆![]() 的焦点为顶点,顶点为焦点,
的焦点为顶点,顶点为焦点,![]() 是双曲线
是双曲线![]() 在第一象限上任
在第一象限上任
意一点,当![]() 取得最大值时,试问是否存在常数
取得最大值时,试问是否存在常数![]() ,使得
,使得![]() 恒成立?若存在求出
恒成立?若存在求出![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由![]()
2005年10月济南市高三统一考试
高三数学(理工类)模拟试题参考答案及评分标准
一![]() ⒈A ⒉D ⒊C
⒋D ⒌B ⒍D
⒎B ⒏A ⒐B
⒑B ⒒D ⒓B
⒈A ⒉D ⒊C
⒋D ⒌B ⒍D
⒎B ⒏A ⒐B
⒑B ⒒D ⒓B
二![]() ⒔
⒔![]() ⒕
⒕![]() ⒖
⒖![]() ⒗①③④
⒗①③④
三![]() ⒘解:⑴由
⒘解:⑴由![]() ,解得
,解得![]() 或
或![]() =
=![]() ………………4分
………………4分
∵![]() ∴
∴![]() ………………………6分
………………………6分
⑵原式=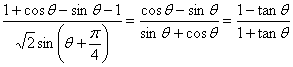 ………………………10分
………………………10分
∴原式=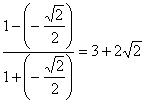 ………………………………………………12分
………………………………………………12分
⒙解:⑴红色骰子投掷所得点数为![]() 是随即变量,其分布如下:
是随即变量,其分布如下:

![]() 8 2
8 2
……………………2分
P ![]()
![]()
E![]() =8·
=8·![]() +2·
+2·![]() =4
……………………………………………………4分
=4
……………………………………………………4分
蓝色骰子投掷所得点数![]() 是随即变量,其分布如下:
是随即变量,其分布如下:

![]() 7 1
7 1
…………………6分
P ![]()
![]()
E![]() =7·
=7·![]() +1·
+1·![]() =4
………………………………………8分
=4
………………………………………8分
⑵∵投掷骰子点数较大者获胜,∴投掷蓝色骰子这若获胜,则投掷后蓝色骰子点数为7,
红色骰子点数为2,∴投掷蓝色骰子获胜概率是![]() =
=![]() ·
·![]() =
=![]() ………………12分
………………12分
19.⑴∵![]() 平面
平面![]() ……………………………3分
……………………………3分
∴平面![]() 平面
平面 ![]() ……………………………………………………5分
……………………………………………………5分
⑵作![]() 于
于![]() ,由⑴知平面
,由⑴知平面![]() 平面
平面![]()
∴![]() 平面
平面![]() ,连接
,连接![]() ……………………………………………………7分
……………………………………………………7分
∴![]() 为直线
为直线![]() 与
与![]() 所成角
……………………………8分
所成角
……………………………8分
∵四边形![]() 是菱形且
是菱形且![]()
∴![]() ,且
,且![]() 为
为![]() 中点,又
中点,又![]() ………………………10分
………………………10分
∴![]() ∴直线
∴直线![]() 与平面
与平面![]() 所成角的正切为
所成角的正切为![]() ……12分
……12分
⒛解:⑴![]() ……………………………………1分
……………………………………1分
∵![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ……………………………………4分
……………………………………4分
⑵要使![]() 在
在![]() 上单调递减,则对
上单调递减,则对![]()
![]() 总有
总有![]() ………6分
………6分
∵![]() ,∴当
,∴当![]() 时,即
时,即![]() ,
,![]() 在
在
![]() 上的最大值为
上的最大值为![]() 或
或![]() …………………………8分
…………………………8分
∵当![]() 时,
时,![]() =10-4
=10-4![]() ≤10
≤10![]() ,
,![]() ………………………11分
………………………11分
∴对![]()
![]() 总有
总有![]()
∴当![]() 时,
时,![]() 在
在![]() 上单调递减 ………………………12分
上单调递减 ………………………12分
21![]() ⑴∵
⑴∵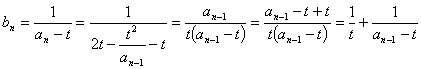
=![]() 为等差数列
……………………6分
为等差数列
……………………6分
⑵∵![]() …………………………………………7分
…………………………………………7分
∴![]() 又
又![]() 是首项为2,公比为2的等比数列
是首项为2,公比为2的等比数列
即![]() …………………………………………9分
…………………………………………9分
则![]()
![]() …………………12分
…………………12分
22![]() 解:⑴设
解:⑴设![]() ,又
,又![]()
∴![]()
又![]() 得
得 ![]()
∴![]() …………………3分
…………………3分
∴当![]() 时
时![]() ,
,![]() …5分
…5分
∴![]() ,即
,即![]() ∴
∴![]() …………………6分
…………………6分
⑵当![]() 时,
时,![]() ∴
∴![]()
![]()
设![]() ,则
,则![]() …………………8分
…………………8分
当![]() 轴时,
轴时,![]() 则
则![]()
故![]() ,猜想
,猜想![]() ,使
,使![]() 总成立………10分
总成立………10分
当![]() 时,
时,![]()
∴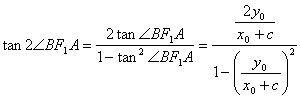 …………………12分
…………………12分
又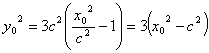
∴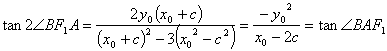 ………13分
………13分
又![]() 与
与![]() 同在
同在![]() 内
内
∴![]() =
=![]()
故存在![]() ,使
,使![]() 恒成立………………………………………10分
恒成立………………………………………10分