|
江苏省扬州中学
2005—2006学年度上学期高三年级期中考试
数 学 试 卷
一、选择题（本大题共12小题，每小题5分，共60分）
1．已知p：x＞0；q：x2＞0，那么 （ ）
A．p是q的必要不充分条件
B．p是q的充分不必要条件
C．p是q的充要条件
D．p既不是q的充分条件，也不是q的必要条件
2．若
，当
＞1时，
的大小关系是 （ ）
A．
B．
C．
D．
3．在数列
中，
，则下列乘积中是负数的是 （ ）
A．
B．
C．
D．
4．若数列是等比数列，则数列
（ ）
A．一定是等比数列 B．一定是等差数列
C．一定不是等差数列
D．以上都不正确
5．已知
，且
，则
与
的夹角是 （ ）
A．150° B．135° C．120° D．60°
6．在锐角
中，若
，则
的范围是 （ ）
A．（0，2） B．（
） C．（
） D．（
）
7．
的值是 （ ）
A．
B．
C．
D．
8．已知
≤≤
，向量
，则
的 （ ）
A．最大值是1，最小值是－1 B．最大值是1，最小值是
C．最大值是2，最小值是－2 D．最大值是2，最小值是－1
9．设M是圆
上的点，则M点到直线
的最大距离是（ ）
A．9 B．8 C．5 D．2
10．不等式组
，表示的平面区域的面积是 （ ）
A．12 B．24 C．36 D．48
11．在直角坐标平面上，向量
（4，1），向量
（2，－3），两向量在直线
上的正射影长度相等，则直线的斜率为 （ ）
A．2 B． C．2或 D．3或
12．已知直线：
和圆M：
，
为直线上一点，
、
为圆M上两点，在中，
，边
过圆心M，则点的横坐标的取值范围是 （ ）
A．[－3，3] B．[3，6] C．[－6，6] D． [0，9]
二、填空题（本大题共6小题，每小题4分，共24分）
13．过点P（1，2）且与原点距离最大的直线方程是______________．
14．函数
的递增区间为________________．
15．若数列中，
，则该数列的前19项的和
=_____________．
16．若指数函数
的部分对应值如下表：
|
| －2 | 0 | 2 |
|
| 0.694 | 1 | 1.44 |
则不等式
的解集是_______________________．
17．与圆
切于点（3，6），且过点（5，6）的圆的方程是
___________________．
18．实系数方程
的一个根大于0且小于1，另一根大于1且小于2，则
的
取值范围是______________．
三、解答题（本大题共5小题，共66分）
19．（本小题12分）
已知数列的前
项和
，且
．
⑴求数列的通项公式．
⑵求数列
的前项和．
20．（本小题12分）
已知函数
的反函数为
（
且
），求的解
析式及其定义域．
21．（本小题12分）
⑴已知
是正常数，
、
（0，+∞）．求证：
≥
，指出等号成
立的条件．
⑵利用⑴的结论求函数
，
的最小值，指出取最小值时的值．
22．（本小题14分）
已知向量
，且
，设
．
⑴求及
．
⑵若
的最小值是
，求
的值．
⑶若方程
有解，求的取值范围．
23．（本小题16分）
已知数列中，
，且
．
⑴若
，求证：数列
是等比数列．
⑵求数列的通项公式．
⑶若
，求证：
…
＜
．
高三数学期中试卷参考答案
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | B | A | D | C | D | C | D | B | B | D | B |
13. x+2y－5=0 14.
15.－382 16.（0，1）∪（1，2） 17.
18.
三、解答题（本大题共5小题，共66分）
19．⑴
，
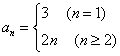
⑵
时，
∴
…
…
，
又
，满足此式，∴
．
20．由
得
，又
，
∴
，∴
，对于
，由
得
或
，当时，
，时，
，∴当
时
的定义域为
，
当
时，的定义域为
．
21．⑴∵
、
，
、
，
∴
≥
∴
≥
等号成立的条件是
⑵当
时，
，
，
，
当
，即
时，取得最小值25．
22．⑴
⑵
当
时，
（舍去），
当
时，
，
当
时，
，综上可知
．
⑶即方程
，在
时有解，又
不满足方程，∴
，∴
，
∵
在
时单调递增，∴
，∴
，∴
．
23．⑴由已知得
，∴
，∴
是首
项为
，公比为
的等比数列．
⑵由⑴得
，即
，
∴
，
，…
，∴
，∴
，又
时，
…
，∴
，
综上可知
．
⑶由
得
，
∵
，又
，∴
，
，∴
，∴
，∴
，∴
，
∴
…
…
…
．
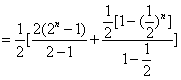