北 京 四 中
2005年数学第三次统测(理科)
一、选择题:(每小题5分)
1. 在正实数集上定义一种运算*:当![]() 时,a*b=b3:当
时,a*b=b3:当![]() 时,a*b=b2。根据这个定义,满足3*x=27的x的值为( )
时,a*b=b2。根据这个定义,满足3*x=27的x的值为( )
A.3 B.1或9 C.1或![]() D.3或
D.3或![]()
2. 函数![]() 的部分图象大致是( )
的部分图象大致是( )
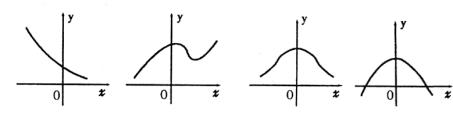
A. B. C. D.
3. 在![]() 的展开式中,含
的展开式中,含![]() 项的系数是首项为-2公差为3的等差数列的( )
项的系数是首项为-2公差为3的等差数列的( )
A.第13项 B.第18项 C.第11项 D.第20项
4. 若将函数![]() 的图象按向量
的图象按向量![]() 平移,使图象上点P的坐标由(1,0)变为(2,2),则平移后图象的解析式为( )
平移,使图象上点P的坐标由(1,0)变为(2,2),则平移后图象的解析式为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5. 一平面截一球得到直径是6cm的圆面,球心到这个平面的距离是4cm,则该球的体积是( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 已知函数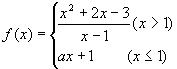 在点
在点![]() 处连续,则
处连续,则![]() 的值是( )
的值是( )
A.2 B.3 C.-2 D.-4
7. 已知![]() ,
,![]() ,点C在坐标轴上,若
,点C在坐标轴上,若![]() ,则这样的点C的个数为( )
,则这样的点C的个数为( )
A.1 B.2 C.3 D.4
8. 设数集![]()
![]() ,
,![]()
![]() ,且
,且![]() 都是集合
都是集合![]() 的子集,如果把
的子集,如果把![]() 叫做集合
叫做集合![]() 的“长度”,那么集合
的“长度”,那么集合![]() 的“长度”的最小值是( )
的“长度”的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:(每小题5分)
9. 若![]() (m∈R+)是纯虚数,则
(m∈R+)是纯虚数,则![]() 的值为_____,
的值为_____,![]() 的虚部是_____.
的虚部是_____.
10. 在数列![]() 中,若
中,若![]() 且对任意
且对任意![]() 有
有![]() 则数列
则数列![]() 前
前![]() 项的和为_____,前
项的和为_____,前![]() 项和最小时的
项和最小时的![]() 等于_____.
等于_____.
11. 若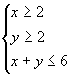 ,则目标函数
,则目标函数![]() 的取值范围是_____.
的取值范围是_____.
12. 向量a、b满足(a-b)·(2a+b)=-4,且a=2,b=4,则a与b夹角的余弦值等于_____.
13. 已知P是抛物线![]() 上的动点,定点A(0,-1),若点M分
上的动点,定点A(0,-1),若点M分![]() 所成的比为2,则点M的轨迹方程是
所成的比为2,则点M的轨迹方程是
_____,它的焦点坐标是_________.
14. 若定义在区间D上的函数![]() 对于D上的任意n个值
对于D上的任意n个值![]() ,总满足
,总满足![]() ,则
,则![]() 称为D上的凸函数. 现已知
称为D上的凸函数. 现已知![]() 在
在![]() 上是凸函数,则锐角
上是凸函数,则锐角![]() 中,
中,![]() 的最大值是_________.
的最大值是_________.
答 案
一、选择题:(每小题5分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
|
|
|
|
|
|
|
|
二、填空题:(每小题5分)
| 9 |
|
| 10 |
|
| |||
| 11 |
| 12 |
| |||||
| 13 |
|
| 14 |
| ||||
三、解答题
15. (本小题满分13分)
矩形ABCD,AB=4,BC=3,E为DC中点,沿AE将ΔAED折起,使二面角D-AE-B为60°。
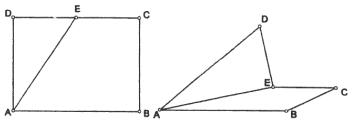
(I)求DE与平面AC所成角的大小;
(II)求二面角D-EC-B的大小。
16. (本小题满分13分)
甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6道题,乙能答对其中的8道题,规定每位考生都从备选题中随机抽出3道题进行测试,至少答对2道题才算合格。
(1) 求甲、乙两人考试合格的概率分别是多少?
(2) 求乙答对试题数![]() 的概率分布及数学期望。
的概率分布及数学期望。
17. (本小题满分14分)
设函数![]() 在
在![]() 时取得极值.
时取得极值.
(1)试确定![]() 的值;
的值;
(2)求![]() 的单调区间.
的单调区间.
18. (本小题满分14分)
已知函数![]() .
.
(1) 求![]() 的值,使点
的值,使点![]() 到直线
到直线![]() 的距离最短为
的距离最短为![]() ;
;
(2) 若不等式![]() 在
在![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
19. (本小题满分13分)
直线![]() 与曲线
与曲线![]() 交于
交于![]() (
(![]() 异于原点
异于原点![]() );过
);过![]() 且斜率为
且斜率为![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() (
(![]() 异于
异于![]() );过
);过![]() 且斜率为
且斜率为![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() (
(![]() 异于
异于![]() ),……, 过
),……, 过![]() 且斜率为
且斜率为![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() (
(![]() 异于
异于![]() ),……。设
),……。设![]() 坐标为
坐标为![]() ,(
,(![]() ).
).
(Ⅰ)求![]() 和
和![]() 的表达式;
的表达式;
(Ⅱ)判定![]() 是否存在,若存在,求它的值;若不存在,说明理由.
是否存在,若存在,求它的值;若不存在,说明理由.
20. (本小题满分13分)
已知![]() 为椭圆
为椭圆![]() 和双曲线
和双曲线![]() 的公共顶点,
的公共顶点,![]() 分别为双曲线和椭圆上不同于
分别为双曲线和椭圆上不同于![]() 的动点,且有
的动点,且有![]() ,设
,设![]() 的斜率分别是
的斜率分别是![]() .
.
(1)求证![]() ;
;
(2)设![]() 分别为双曲线和椭圆的右焦点,若
分别为双曲线和椭圆的右焦点,若![]() ∥
∥![]() ,求
,求![]() 的值.
的值.
答案
一、选择题:(每小题5分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | D | C | D | C | C | B | C | C |
二、填空题:(每小题5分)
| 9 |
| -8 | 10 |
| 4或5 | |||
| 11 | [8,14] | 12 |
| |||||
| 13 | y=6x2-1(x≠0) |
| 14 |
| ||||
15.如图1,过点D作DM⊥AE于M,延长DM与BC交于N,在翻折过程中DM⊥AE,MN⊥AE保持不变,翻折后,如图2,∠DMN为二面角D-AE-B的平面角,∠DMN=60°,AE⊥平面DMN,又因为AE![]() 平面AC,则平面AC⊥平面DMN。
平面AC,则平面AC⊥平面DMN。
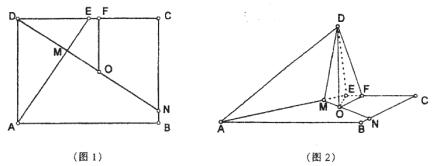
(I)在平面DMN内,作DO⊥MN于O,
∵平面AC⊥平面DMN,
∴DO⊥平面AC。
连结OE,DO⊥OE,∠DEO为DE与平面AC所成的角
如图1,在直角三角形ADE中,AD=3,DE=2,
![]() ,
,
![]() 。
。
如图2,在直角三角形DOM中,DO=DM·sin60°=![]() ,
,
在直角三角形DOE中,![]() ,则
,则![]() 。
。
∴DE与平面AC所成的角为![]() 。
。
(II)如图2,在平面AC内,作OF⊥EC于F,连结DE,
∵DO⊥平面AC,∴DF⊥EC,∴∠DFO为二面角D-EC-B的平面角。
如图1,作OF⊥DC于F,则RtΔEMD∽RtΔOFD,![]() ,∴
,∴![]() 。
。
如图2,在RtΔDOM中,OM=DMcos∠DMO=DM·cos60°=![]() .
.
如图1,DO=DM+MO![]() 。
。
在RtΔDFO中,![]() ,
,
∴二面角D-EC-B的大小为![]() 。
。
16. 解:(1)设甲、乙两人考试合格的事件分别为A、B
则![]()
![]()
(2)乙答对试题数ξ的可能值为1,2,3
则![]()
![]()
![]()
∴ξ的概率分布为
| ξ | 1 | 2 | 3 |
| P |
|
|
|
![]()
17.(1)![]()
![]()
∵f(x)在x1=1,x2=2时取得极值
∴ 
(2)由(1)可得:![]()
令![]() ∴ x<0或1<x<2
∴ x<0或1<x<2
∵ ![]() ∴ 1<x<2
∴ 1<x<2
∴ f(x)的单调增区间为(1,2),减区间是(0,1)和(2,+![]() )
)
18. 解:(1)由题意得M到直线x+y-1=0的距离![]()
令![]()
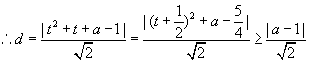
![]()
解得a=3或a=-1(舍去)
∴a=3
(2)由![]()
得![]()
也就是![]()
令![]()
即at2-2t+a2≤0在t∈[1,2]上恒成立
设![]() ,则要使上述条件成立,只需
,则要使上述条件成立,只需![]()
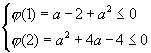 解得
解得![]()
即满足题意的a的取值范围是![]()
19.解:(Ⅰ)由已知![]()
![]() ,
,
设![]()
![]() ,其中
,其中![]() ,
,
解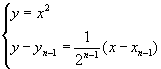 (注意到
(注意到![]() )得
)得![]() ,
,
x1=1
于是,![]() ;
;
![]() ;
;
![]() ;
;
猜测 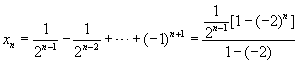
![]()
![]()
当![]() 时,
时,![]() ,猜测正确,
,猜测正确,
假设当![]() 时,
时,![]()
![]() 成立,即
成立,即![]()
![]()
那么,当![]() 时,
时,![]()
![]()
![]()
综上所述,![]()
![]()
![]() .
.
(Ⅱ)![]()
![]()
![]() .
.
所以,![]()
![]() .
.
20. 解:(1)A(-a,0),B(a,0),设P(x1,y1)Q(x2,y2)
则![]()
![]()
![]()
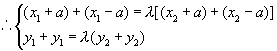
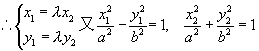
![]()
![]()
![]()
![]()
(2)![]()
由(1)![]()
![]() 又P在双曲线上
又P在双曲线上
![]()
![]()
同理![]()
![]()