2006届闵行三中高三期末强化卷(四)
学号: 姓名:
一、填空题:
1、一人口袋里装有大小相同的![]() 个小球,其中红色、黄色、绿色的球各
个小球,其中红色、黄色、绿色的球各![]() 个。如果任意取出
个。如果任意取出![]() 个小球,那么其中恰有
个小球,那么其中恰有![]() 个小球同颜色的概率是 (用分数表示)。
个小球同颜色的概率是 (用分数表示)。
2、某学校的某一专业从8名优秀毕业生中选派5名支援中国西部开发建设, 其中甲同学必须被选派的概率是_ __.
3、将7名学生分配到甲、乙两个宿舍中, 每个宿舍至少安排2名学生, 那么互不相同的分配方案共有_ __ 种.
4、若集合![]() ,
,![]() ,则
,则![]() = .
= .
5、不等式![]() 的解为
。
的解为
。
6、设![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,则
,则![]() 。
。
7将函数![]() 的图像向左平移一个单位后得到
的图像向左平移一个单位后得到![]() 的图像,再将
的图像,再将![]() 的图像绕原点旋转
的图像绕原点旋转![]() 后仍与
后仍与![]() 的图像重合,则
的图像重合,则![]() 。
。
8、求![]()
 9、若奇函数
9、若奇函数![]() ,当
,当![]() 时,
时,![]() ,则不等式
,则不等式![]() 的解为
。
的解为
。
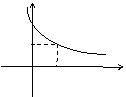
10、函数![]() 的图象如图所示,它在R上单调递减,现有如下结论:
的图象如图所示,它在R上单调递减,现有如下结论:
⑴![]() ;⑵
;⑵![]() ;⑶
;⑶![]() ;⑷
;⑷![]() 。
x
。
x
其中正确的命题序号为______________.(写出所有正确命题序号)
二、选择题:
11、若函数![]() 、
、![]() 的定义域和值域都是
的定义域和值域都是![]() ,则“
,则“![]() ”成立的充要条件是( )
”成立的充要条件是( )
(A)存在![]() ,使得
,使得![]() (B)有无数多个实数
(B)有无数多个实数![]() ,使得
,使得![]()
(C)对任意![]() ,都有
,都有![]() (D)不存在实数
(D)不存在实数![]() ,使得
,使得![]()
12、 在△![]() 中,若
中,若![]() ,则△
,则△![]() 是 ( )
是 ( )
(A)直角三角形. (B)等边三角形.
(C)钝角三角形. (D)等腰直角三角形.
13、若函数![]() 在区间
在区间![]() 上是减函数,则
上是减函数,则![]() 的取值范围可用区间表示为( )
的取值范围可用区间表示为( )
![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]() 。
。
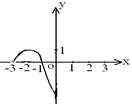
14、如果![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,![]() 的
的
图象如图所示,那么不等式![]() 的解集为( )
的解集为( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
三、解答题:
15、某市2004年底有住房面积1200万平方米,计划从2005年起,每年拆除20万平方米的旧住房. 假定该市每年新建住房面积是上年年底住房面积的5%.
(1)分别求2005年底和2006年底的住房面积 ;
(2)求2024年底的住房面积.(计算结果以万平方米为单位,且精确到0.01)
16、已知:![]() ,且
,且![]() 求
求![]() 的值。
的值。
17、命题甲: ![]() R, 关于x的方程
R, 关于x的方程![]() 有两个非零实数解;
有两个非零实数解;
命题乙: ![]() R, 关于x的不等式
R, 关于x的不等式![]() 的解集为空集; 当甲、乙中有且仅有一个为真命题时, 求实数a的取值范围.
的解集为空集; 当甲、乙中有且仅有一个为真命题时, 求实数a的取值范围.
18、设![]()
(1)求![]() 的反函数
的反函数![]() :
:
(2)讨论![]() 在
在![]() 上的单调性,并加以证明:
上的单调性,并加以证明:
(3)令![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上的值域是
上的值域是![]() ,求
,求![]() 的取值范围。
的取值范围。
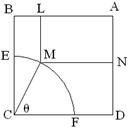
19、如图,某小区有一块边长为50米的正方形空地![]() ,其中
,其中![]() 是一个以
是一个以![]() 为圆心,
为圆心,![]() 为半径的扇形,
为半径的扇形,![]() 分别在
分别在![]() 上,在此拟建水池与人行道;
上,在此拟建水池与人行道;![]() 为一矩形,
为一矩形,![]() 分别在
分别在![]() 上,
上,![]() 在弧
在弧![]() 上,在此拟建活动中心;其余部分为绿化区域,设
上,在此拟建活动中心;其余部分为绿化区域,设![]() =
=![]() ,绿化区域的面积为
,绿化区域的面积为![]() 。
。
 (1)当
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数解析式
的函数解析式![]() ,并求当
,并求当![]() 取最大值时相应的
取最大值时相应的![]() 的值(精确到0.001);
的值(精确到0.001);
(2)当![]() 米时,求
米时,求![]() 的最大值(精确到0.001)。
的最大值(精确到0.001)。
20、.数列{an}满足an=3an-1+3n-1 (n³2),且a3=95。
(1) 求a1,a2;
(2) 是否存在一个实数t,使得![]() (nÎZ+),{bn}为等差数列。有,则求出t,并予以证明;没有,则说明理由;
(nÎZ+),{bn}为等差数列。有,则求出t,并予以证明;没有,则说明理由;
(3) 求数列{an}的前n项和Sn。
21、已知函数![]()
(1)求f(x)的反函数f-1(x);
(2)设![]()
(3)设![]() ,是否存在最小正整数m,使对任意
,是否存在最小正整数m,使对任意![]() ,都有
,都有![]() 成立?若存在,求出m的值,若不存在说明理由。
成立?若存在,求出m的值,若不存在说明理由。
22、 已知![]() ,
,![]() 分别是与x轴、y轴正方向相同的单位向量,
分别是与x轴、y轴正方向相同的单位向量,![]()
![]() ,对任意正整数n,
,对任意正整数n,![]() 。
。
(1)若![]() ,求a的值;
,求a的值;
(2)求向量![]() ;
;
(3)设向量![]()
![]() ,求最大整数a的值,使对任意正整数n,都有
,求最大整数a的值,使对任意正整数n,都有![]() 成立。
成立。
2006届闵行三中高三期末强化卷(四)
一、填空题:
1、一人口袋里装有大小相同的![]() 个小球,其中红色、黄色、绿色的球各
个小球,其中红色、黄色、绿色的球各![]() 个。如果任意取出
个。如果任意取出![]() 个小球,那么其中恰有
个小球,那么其中恰有![]() 个小球同颜色的概率是
个小球同颜色的概率是 ![]() (用分数表示)。
(用分数表示)。
2、某学校的某一专业从8名优秀毕业生中选派5名支援中国西部开发建设, 其中甲同学必须被选派的概率是_ ![]() _.
_.
3、将7名学生分配到甲、乙两个宿舍中, 每个宿舍至少安排2名学生, 那么互不相同的分配方案共有_112 __ 种.
4、若集合![]() ,
,![]() ,则
,则![]() =
= ![]() .
.
5、不等式![]() 的解为
的解为 ![]() 。
。
6、设![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,则
,则![]()
![]() 。
。
7将函数![]() 的图像向左平移一个单位后得到
的图像向左平移一个单位后得到![]() 的图像,再将
的图像,再将![]() 的图像绕原点旋转
的图像绕原点旋转![]() 后仍与
后仍与![]() 的图像重合,则
的图像重合,则![]()
![]() 。
。
8、求![]()
![]()
 9、若奇函数
9、若奇函数![]() ,当
,当![]() 时,
时,![]() ,则不等式
,则不等式![]() 的解为
的解为 ![]() 。
。
10、函数![]() 的图象如图所示,它在R上单调递减,现有如下结论:
的图象如图所示,它在R上单调递减,现有如下结论:
![]()
⑴![]() ;⑵
;⑵![]() ;⑶
;⑶![]() ;⑷
;⑷![]() 。
0 1 x
。
0 1 x
其中正确的命题序号为__⑵_⑶__⑷__.(写出所有正确命题序号)
二、选择题:
11、若函数![]() 、
、![]() 的定义域和值域都是
的定义域和值域都是![]() ,则“
,则“![]() ”成立的充要条件是 ( D )
”成立的充要条件是 ( D )
(A)存在![]() ,使得
,使得![]() (B)有无数多个实数
(B)有无数多个实数![]() ,使得
,使得![]()
(C)对任意![]() ,都有
,都有![]() (D)不存在实数
(D)不存在实数![]() ,使得
,使得![]()
12、 在△![]() 中,若
中,若![]() ,则△
,则△![]() 是 (B )
是 (B )
(A)直角三角形. (B)等边三角形.
(C)钝角三角形. (D)等腰直角三角形.
13、若函数![]() 在区间
在区间![]() 上是减函数,则
上是减函数,则![]() 的取值范围可用区间表示为( C )
的取值范围可用区间表示为( C )

![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]() 。
。
14、如果![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,![]() 的
的
图象如图所示,那么不等式![]() 的解集为( D )
的解集为( D )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
三、解答题:
15、某市2004年底有住房面积1200万平方米,计划从2005年起,每年拆除20万平方米的旧住房. 假定该市每年新建住房面积是上年年底住房面积的5%.
(1)分别求2005年底和2006年底的住房面积 ;
(2)求2024年底的住房面积.(计算结果以万平方米为单位,且精确到0.01)
[解](1)2005年底的住房面积为![]() (万平方米),
(万平方米),
2006年底的住房面积为![]() (万平方米)
(万平方米)
∴ 2005年底的住房面积为1240万平方米,2006年底的住房面积约为1282万平方米
(2)2024年底的住房面积为
![]()
![]() (万平方米)
(万平方米)
∴ 2024年底的住房面积约为2522.64万平方米.
16、已知:![]() ,求
,求![]() 的值。
的值。
解:![]() ,
,![]()
18.命题甲: ![]() R, 关于x的方程
R, 关于x的方程![]() 有两个非零实数解;
有两个非零实数解;
命题乙: ![]() R, 关于x的不等式
R, 关于x的不等式![]() 的解集为空集; 当甲、乙中有且仅有一个为真命题时, 求实数a的取值范围.
的解集为空集; 当甲、乙中有且仅有一个为真命题时, 求实数a的取值范围.
解:当甲真时,设![]()
![]() ,即两函数图象有两个交点.
,即两函数图象有两个交点.
则![]()
当乙真时,![]() 时 满足 或
时 满足 或![]() 也满足 则
也满足 则![]()
∴当甲乙有但仅有一个为真命题时,即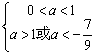 或
或
∴![]()
17、设![]()
(1)求![]() 的反函数
的反函数![]() :
:
(2)讨论![]() 在
在![]() 上的单调性,并加以证明:
上的单调性,并加以证明:
(3)令![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上的值域是
上的值域是![]() ,求
,求![]() 的取值范围。
的取值范围。
解:(1)![]()
(2)设![]() ,∵
,∵![]()
∴![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上是减函数:
上是减函数:
![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上是增函数。
上是增函数。
(3)当![]() 时,∵
时,∵![]() 在
在![]() 上是减函数
上是减函数
∴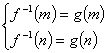 ,由
,由![]() 得
得![]() ,即
,即![]() 可知方程的两个根均大于
可知方程的两个根均大于![]() ,即
,即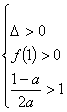
![]()
当![]() 时,∵
时,∵![]() 在
在![]() 上是增函数
上是增函数
∴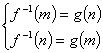
![]()
![]() (舍去)。
(舍去)。
综上,得 ![]() 。
。
18、(本题14分)如图,某小区有一块边长为50米的正方形空地![]() ,其中
,其中![]() 是一个以
是一个以![]() 为圆心,
为圆心,![]() 为半径的扇形,
为半径的扇形,![]() 分别在
分别在![]() 上,在此拟建水池与人行道;
上,在此拟建水池与人行道;![]() 为一矩形,
为一矩形,![]() 分别在
分别在![]() 上,
上,![]() 在弧
在弧![]() 上,在此拟建活动中心;其余部分为绿化区域,设
上,在此拟建活动中心;其余部分为绿化区域,设![]() =
=![]() ,绿化区域的面积为
,绿化区域的面积为![]() 。
。
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数解析式
的函数解析式![]() ,并求当
,并求当![]() 取最大值时相应的
取最大值时相应的![]() 的值(精确到0.001);
的值(精确到0.001);
 (2)当
(2)当![]() 米时,求
米时,求![]() 的最大值(精确到0.001)。
的最大值(精确到0.001)。
(1)解:![]()
![]()
![]() ,
,![]()
![]() 取最大值时,
取最大值时,![]() 28.029(米)。
28.029(米)。
(2)解:![]()
![]()
![]()
令![]() ,
,![]() ,则
,则![]()
![]()
![]()
![]() (平方米)
(平方米)
19、.数列{an}满足an=3an-1+3n-1 (n³2),且a3=95。
(1) 求a1,a2;
(2) 是否存在一个实数t,使得![]() (nÎZ+),{bn}为等差数列。有,则求出t,并予以证明;没有,则说明理由;
(nÎZ+),{bn}为等差数列。有,则求出t,并予以证明;没有,则说明理由;
(3) 求数列{an}的前n项和Sn。
解: (1) a1=5,a2=23。
(2) ![]() 为等差数列,必须
为等差数列,必须![]() ,
,![]() ,
,![]() 成等差,得
成等差,得![]() 。即
。即![]() ,当n=1,2,3成等差。
,当n=1,2,3成等差。
下证此时bn对一切nÎZ+定成等差数列。
![]()
\当![]() 时,{bn}是公差为1的等差数列。
时,{bn}是公差为1的等差数列。
(3) ![]() ,\
,\![]() 。
。
由![]()
得:![]()
错位相减,得![]() 。
。
20、已知函数![]()
(1)求f(x)的反函数f-1(x);
(2)设![]()
(3)设![]() ,是否存在最小正整数m,使对任意
,是否存在最小正整数m,使对任意![]() ,都有
,都有![]() 成立?若存在,求出m的值,若不存在说明理由。
成立?若存在,求出m的值,若不存在说明理由。
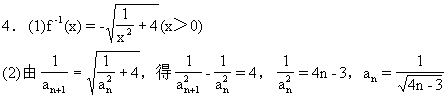
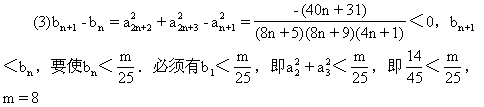
22、已知![]() ,
,![]() 分别是与x轴、y轴正方向相同的单位向量,
分别是与x轴、y轴正方向相同的单位向量,![]()
![]() ,对任意正整数n,
,对任意正整数n,![]() 。
。
(1)若![]() ,求a的值;
,求a的值;
(2)求向量![]() ;
;
(3)设向量![]()
![]() ,求最大整数a的值,使对任意正整数n,都有
,求最大整数a的值,使对任意正整数n,都有![]() 成立。
成立。
解:(1) 由题意![]()
![]() . ,所以51a+12=0,解得
. ,所以51a+12=0,解得![]() 。
。
(2) ![]() =
=![]()
![]()
(3) ![]() ,
,![]() ,由
,由![]() 恒成立,得
恒成立,得![]() 恒成立,令
恒成立,令![]() ,只需求数列
,只需求数列![]() 的最小项。
的最小项。
由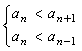 得
得![]() ,即n=6,
,即n=6,![]() ,所以
,所以 ![]() 。
。