2006届闵行三中高三期末强化卷（一）
学号： 姓名：
一、填空题（共12小题，每小题3分，满分36分）
1．已知直线
，则直线
的倾斜角为
（用反三角表示）。
2．
。
3．在△
中，若
，
，则
。
4．函数
的反函数
。
5．若关于
的不等式
的解集不是空集，则实数
的取值范围是_______。
6．若
是实系数一元二次方程
的一个根，则
。
7．已知向量
，且A、B、C三点共线，则k= 。
8．若 
, 
，且
为纯虚数，则实数的值为
。
9．设数列｛an｝是公比q＞0的等比数列，Sn是它的前n项和，若
Sn＝7，则此数列的首项a1的取值范围是 。
10． 函数
的值域是
。
11．若
则
。
12．已知等差数列
，若数列
满足
，则数列也是等差数列，类比这一性质，相应地已知等比数列
中，
，若
=
，则数列
也是等比数列。
二、选择题（共4小题，每小题4分，满分16分）
13．已知向量
，且
，则由x的值构成的集合是（ ）
（A）{2，3} （B）{－1，6} （C）{2} （D）{6}
14．设集合A、B是全集
的两个子集，则
是
的 （ ）
（A）充分不必要条件（B）必要不充分条件（C）充要条件（D）既不充分也不必要条件
15．设函数
为定义域在R上的以3为周期的奇函数，若
，则（ ）
（A）
(B)
(C)
(D)
16．某工厂投入98万元购买一套设备，第一年的维修费用12万元，以后每年增加4万元，每年可收入50万元．就此问题给出以下命题：①前两年没能收回成本；②前5年的平均年利润最多；③前10年总利润最多；④第11年是亏损的；⑤10年后每年虽有盈利但与前10年比年利润有所减少．（总利润=总收入－投入资金－总维修费）其中真命题是
（ ）
(A)①②⑤ (B)①③⑤ (C)①③④ (D)②③④
三、解答题（共5小题，满份48分）
17．(本题满分8分)已知
是复数，
均为实数（
为虚数单位），且复数
在复平面上对应的点在第三象限，求实数的取值范围。
18．(本题满分10分)设锐角
ABC中，
.
(1)求
A的大小； (2)求
取最大值时，B的大小。
18.解：(1)因为2sin2A-cos2A=2 所以cos2A=
，所以 A=
。
(2)y=2sin2B+sin(2B+
)=1+sin(2B-)
因为0<2B<
所以当2B-=
即B=时，
。
19．(本题满分10分)设函数
，不等式
的解集为（－1，2）
（Ⅰ）判断
的单调性，并用定义证明；
（Ⅱ）解不等式
。
19. 解：因为
得
又因为
的解集为（－1，2） 所以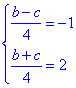
得b=2。
（Ⅰ）函数
在
上为增函数。
证明：设
，则
因为 ，所以
所以
即
，所以，函数在
上为增函数。
（Ⅱ）由
得
。
①当
，即
时，
；②当
，即
时，无解
③当
，即
时，
所以，当时，解集为
； 当时，解集为空集；
当时，解集为
。
20．(本题满分10分)设数列{an}的首项a1=a≠
，且
,
记
，n＝＝l，2，3，…·．
（I）求a2，a3；
（II）判断数列{bn}是否为等比数列，并证明你的结论；
（III）求
。
20.解：（I）a2＝a1+=a+，a3=
a2=a+
；
（II）因为 a4=a3+=a+
, 所以a5=a4=a+
,
所以b1=a1－=a－, b2=a3－= (a－), b3=a5－= (a－),
猜想：{bn}是公比为的等比数列。
证明如下：因为bn+1＝a2n+1－=a2n－= (a2n－1－)=bn, (n∈N*)
所以{bn}是首项为a－, 公比为的等比数列·
（III）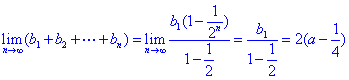
。
21. (本题满分10分)设一次函数的图象关于直线y＝x对称的图象为C，且
．若点（n＋1，
）（n∈N*）在曲线C上，并且a1＝a2＝1。
（Ⅰ）求曲线C的方程；
（Ⅱ）求证：
；
（Ⅲ）设Sn＝
+…＋
，求Sn。
21.解：（Ⅰ）设＝ax＋b（a≠0），则C的方程为：
y＝
(x－b),
由，得－a＋b＝0，………………………………… ①
由点（2，
）在曲线C上，得1＝（2－b）， ………… ②
由①、②解得a＝b＝1，
所以曲线C的方程为y＝x－1。
（Ⅱ）由点（n+1，）在曲线C上，有＝n,
于是
＝（n－1）！，
即
＝（n－1）！。a1＝1， an＝（n－1）！。
（Ⅲ）Sn＝
＝
。
2006届闵行三中高三期末强化卷（一）参考答案：
1.
2.2
3.16 4. 
5. 
或
6.0 7.
8.
9.
10.
11.
12.
13.C 14. A 15. D 16.C 17.
,
.
18.解：(1)因为2sin2A-cos2A=2 所以cos2A=，所以 A=。
(2)y=2sin2B+sin(2B+)=1+sin(2B-)
因为0<2B< 所以当2B-=即B=时，。
19. 解：因为得
又因为的解集为（－1，2） 所以 得b=2。
（Ⅰ）函数在上为增函数。
证明：设，则
因为 ，所以
所以 即，所以，函数在上为增函数。
（Ⅱ）由得。
①当，即时，；②当，即时，无解
③当，即时，
所以，当时，解集为； 当时，解集为空集；
当时，解集为。
20.解：（I）a2＝a1+=a+，a3=a2=a+；
（II）因为 a4=a3+=a+, 所以a5=a4=a+,
所以b1=a1－=a－, b2=a3－= (a－), b3=a5－= (a－),
猜想：{bn}是公比为的等比数列。
证明如下：因为bn+1＝a2n+1－=a2n－= (a2n－1－)=bn, (n∈N*)
所以{bn}是首项为a－, 公比为的等比数列·
（III）。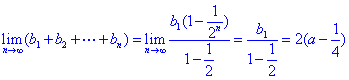
21.解：（Ⅰ）设＝ax＋b（a≠0），则C的方程为：
y＝(x－b),
由，得－a＋b＝0，………………………………… ①
由点（2，）在曲线C上，得1＝（2－b）， ………… ②
由①、②解得a＝b＝1，
所以曲线C的方程为y＝x－1。
（Ⅱ）由点（n+1，）在曲线C上，有＝n,
于是＝（n－1）！，
即＝（n－1）！。a1＝1， an＝（n－1）！。
（Ⅲ）Sn＝
＝。