高三单元试题之八圆锥曲线方程
一、 选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. AB是抛物线y2=2x的一条焦点弦,AB=4,则AB中点C的横坐标是( )
A.2 B.![]() C.
C.![]() D.
D.![]()
2.⊙O1与⊙O2的半径分别为1和2,O1O2=4,动圆与⊙O1内切而与⊙O2外切,则动圆圆心轨迹是( )
A.椭圆 B.抛物线 C.双曲线 D.双曲线的一支
3.双曲线tx2-y2-1=0的一条渐近线与直线2x+y+1=0垂直,则双曲线的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.P是以F1、F2为焦点的椭圆上一点,过焦点F2作∠F1PF2外角平分线的垂线,垂足为M,则点M的轨迹是( )
A.圆 B.椭圆 C.双曲线 D.抛物线
5.若抛物线y2=2px(p>0)与抛物线y2=2q(x-h)(q>0)有公共焦点,则( )
A.2h=p-q B.2h=p+q C.2h=-p-q D.2h=q-p
6.
设双曲线![]() (a,b>0)两焦点为F1、、F2,点Q为双曲线上除顶点外的任一点,过焦点F1作∠F1QF2的平分线的垂线,垂足为P,则P点轨迹是 ( )
(a,b>0)两焦点为F1、、F2,点Q为双曲线上除顶点外的任一点,过焦点F1作∠F1QF2的平分线的垂线,垂足为P,则P点轨迹是 ( )
A.椭圆的一部分; B.双曲线的一部分;
C.抛物线的一部分; D.圆的一部分
7.方程![]() 所表示的曲线为( )
所表示的曲线为( )
A.焦点在x轴上的椭圆 B.焦点在y轴上的椭圆
C.焦点在x轴上的双曲线 D.焦点在y轴上的双曲线
8.我国发射的“神舟四号”宇宙飞船的运行轨道是以地球的中心F2为一个焦点的椭圆,近地点A距地面为m千米,远地点B距地面为n千米,地球半径为R千米,则飞船运行轨道的短轴长为( )
A.![]() B.
B.![]() C.mn千米 D.2mn千米
C.mn千米 D.2mn千米
9.双曲线![]() 的离心率
的离心率![]() ,点A与F分别是双曲线的左顶点和右焦点,B(0,b),则∠ABF等于( )
,点A与F分别是双曲线的左顶点和右焦点,B(0,b),则∠ABF等于( )
A. 45° B. 60° C. 90° D. 120°
10.设F1,F2是双曲线![]() 的两个焦点,P在双曲线上,当△F1PF2的面积为1时,
的两个焦点,P在双曲线上,当△F1PF2的面积为1时,![]() 的值为( )
的值为( )
A.2 B.1 C.![]() D.0
D.0
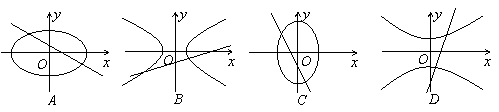 11.设a,b∈R,ab≠0,则直线ax-y+b=0和曲线bx2+ay2=ab的大致图形是 ( )
11.设a,b∈R,ab≠0,则直线ax-y+b=0和曲线bx2+ay2=ab的大致图形是 ( )
12.下列命题正确的是( )
①动点M至两定点A、B的距离之比为常数![]() .则动点M的轨迹是圆。
.则动点M的轨迹是圆。
②椭圆![]() 为半焦距)。
为半焦距)。
③双曲线![]() 的焦点到渐近线的距离为b。
的焦点到渐近线的距离为b。
④已知抛物线y2=2px上两点A(x1,y1),B(x2,y2)且OA⊥OB(O为原点),则y1y2=-p2。
A.②③④ B.①④ C.①②③ D.①③
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
13.已知圆x2+y2-6x-7=0与抛物线y2=2px(p>0)的准线相切,则抛物线的焦点坐标是 。
14.已知椭圆3x2+4y2=12上一点P与左焦点的距离为![]() ,则点P到右准线的距离为 。
,则点P到右准线的距离为 。
15.以双曲线![]() 的右焦点为顶点,左顶点为焦点的抛物线方程是
。
的右焦点为顶点,左顶点为焦点的抛物线方程是
。
16.若平移椭圆4(x+3)2+9y2=36,使平移后的椭圆中心在第一象限,且它与x轴、y轴分别只有一个交点,则平移后的椭圆方程是 ______.
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.在△ABC中,顶点A、B、C所对三边分别为a、b、c,B(-1,0),C(1,0)且b、a、c成等差数列,求顶点A的轨迹方程。
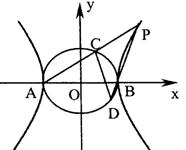
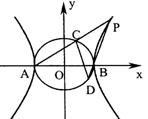
18.如图,椭圆![]() 的左右顶点分别为A、B,P为双曲线
的左右顶点分别为A、B,P为双曲线![]() 右支上(
右支上(![]() 轴上方)一点,连AP交C1于C,连PB并延长交C1于D,且△ACD与△PCD的面积相等,求直线PD的斜率及直线CD的倾斜角.
轴上方)一点,连AP交C1于C,连PB并延长交C1于D,且△ACD与△PCD的面积相等,求直线PD的斜率及直线CD的倾斜角.
|
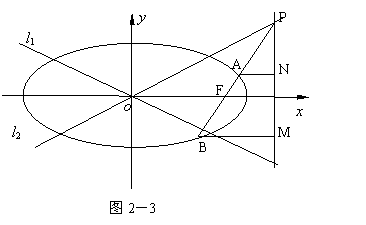 19.已知椭圆C的方程为
19.已知椭圆C的方程为![]() (a>b>0),双曲线
(a>b>0),双曲线![]() 的两条渐近线为l1.l2,过椭圆C的右焦点F作直线l,使l⊥l1,又l与l2交于P点,设l与椭圆C的两交点从左到右依次为B、A(如图2-3),求
的两条渐近线为l1.l2,过椭圆C的右焦点F作直线l,使l⊥l1,又l与l2交于P点,设l与椭圆C的两交点从左到右依次为B、A(如图2-3),求![]() 的最大值及取得最大值时椭圆C的离心率e的值。
的最大值及取得最大值时椭圆C的离心率e的值。
20.(本小题满分12分)已知AB是椭圆![]() 的一条弦,M(2,1)是AB的中点,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线AB交于N(4,-1)
的一条弦,M(2,1)是AB的中点,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线AB交于N(4,-1)
⑴设椭圆和双曲线的离心率分别为![]() 时,求椭圆的方程.
时,求椭圆的方程.
⑵求椭圆长轴长的取值范围.
21.(本小题满分12分)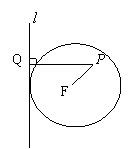 如图,定直线l是半径为3的定圆F的切线,P为平面上一动点,作PQ⊥l于Q,若PQ=2PF.
如图,定直线l是半径为3的定圆F的切线,P为平面上一动点,作PQ⊥l于Q,若PQ=2PF.
⑴点P在怎样的曲线上?并求出该曲线E的标准方程;
⑵过圆心F作直线交曲线E于A、B两点,若曲线E的
中心为O,且![]() , 求点A、B的坐标.
, 求点A、B的坐标.
22.如图,已知线段AB=4,动圆O′与线段AB切于点C,且AC-BC=2![]() ,过点A,
,过点A,
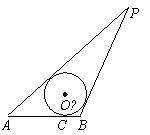 B分别作⊙O′的切线,两切线相交于P,且P、O′均在AB的同侧.
B分别作⊙O′的切线,两切线相交于P,且P、O′均在AB的同侧.
⑴建立适当坐标系,当O′位置变化时,求动点P的轨迹E的方程;
⑵过点B作直线![]() 交曲线E于点M、N,求△AMN的面积的最小值.
交曲线E于点M、N,求△AMN的面积的最小值.
高三单元试题之八:圆锥曲线方程参考答案
一、1.C 2.D 3.B 4.A 5.A 6.D 7.C 8.A 9.C 10.D 11.B 12.C
二、13.(1,0) 14.3 15.![]() 16.4(x-3)2+9(y-2)2=36
16.4(x-3)2+9(y-2)2=36
三、17.解:∵b,a,c成等差数列,∴2a=b+c;又∵a=BC=2,∴b+c=4>a ,即AB+AC=4>BC,则顶点A 的轨迹为椭圆(除长轴顶点)。 由已知得椭圆的c′=1,a′=2,
|
18.解:由题意得C为AP中点,设![]() ,
,![]()
把C点代入椭圆方程、P点代入双曲线方程可得![]()
解之得: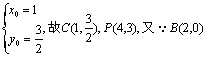
故直线PD的斜率为![]() ,直线PD的方程为
,直线PD的方程为![]()
联立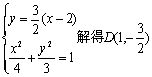 ,故直线CD的倾斜角为90°.
,故直线CD的倾斜角为90°.
19.解:设C的半焦距为c,由对称性,不妨设l1:y=-![]() x,l2:y=
x,l2:y=![]() x
x
由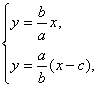 得P(
得P(![]() ,
,![]() ),故点P在椭圆的右准线x=
),故点P在椭圆的右准线x=![]() 上。
上。
设点A内分有向线段![]() 的比为
的比为![]() ,由定比分点坐标公式求出点A的坐标为
,由定比分点坐标公式求出点A的坐标为
 ,
,![]() ),∵点A在椭圆C上,将点A的坐标代入椭圆方程化简.整理得:
),∵点A在椭圆C上,将点A的坐标代入椭圆方程化简.整理得:
(c2+![]() a2)2+
a2)2+![]() 2a4=a2c2(1+
2a4=a2c2(1+![]() )2,两边同除以 a4,由e=
)2,两边同除以 a4,由e=![]() 得(e2+
得(e2+![]() )2+
)2+![]() 2=e2(1+
2=e2(1+![]() )2,∴
)2,∴![]() 2=
2=![]() =-[(2-e2)+
=-[(2-e2)+![]() ]+3≤-2
]+3≤-2![]() +3=3-2
+3=3-2![]() =(
=(![]() -1)2,当且仅当2-e2=
-1)2,当且仅当2-e2=![]() 即e2=2-
即e2=2-![]() 时,
时,![]() max=
max=![]() -1
-1
分别过A、B作椭圆C的右准线的垂线,垂足分别为N、M。
设PB=tPA,可得BM=tAN,∵![]() =e,∴BM=
=e,∴BM=![]() ,同理有AN=
,同理有AN=![]() ,∴BF=tAF
,∴BF=tAF
∴AB=BF+AF=(t+1)AF
又∵AB=PB-PA=(t-1)PA
∴(t+1)AF=(t-1)PA,∴![]() ,又∵
,又∵![]() =
=![]() (∵A为
(∵A为![]() 的内分点)
的内分点)
∴![]() =
=![]() ,由
,由![]() ≤
≤![]() -1,解不等式
-1,解不等式![]() ≤
≤![]() -1,得t≤
-1,得t≤![]() +1, ∴
+1, ∴![]() 的最大值为
的最大值为![]() +1,此时椭圆C的离心率e=
+1,此时椭圆C的离心率e=![]()
20.解:⑴![]() ①
① ![]() ②
②
![]() ③y1+y2=2
④
③y1+y2=2
④
![]() ⑤
⑤
①—②得![]() …*
…*
将③、④、⑤式代入*式,得a2=2b2,c2=b2
![]()
设椭圆的右准线为1,过N作NN′⊥1,则由双曲线定义及题设知.
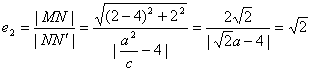
解之,得![]() .
.
当![]() 时,椭圆方程为
时,椭圆方程为![]() 此时点M(2,1)在椭圆外,不可能是椭圆弦的中点,应舍去,故所求椭圆方程为
此时点M(2,1)在椭圆外,不可能是椭圆弦的中点,应舍去,故所求椭圆方程为![]()
⑵由题设知AB方程为y=-x+3,椭圆方程为x2+2y2-a2=0.
由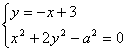 得3x2-12x+18-a2=0(8分)
得3x2-12x+18-a2=0(8分)
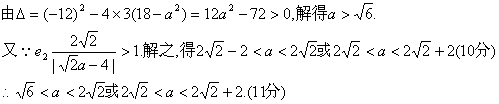
故椭圆长轴2a取值范围是![]()
21.解:⑴∵F为定点,l为定直线,![]()
∴由椭圆第二定义可知,P点在以F为左焦点,l为左准线的椭圆上。
依题意知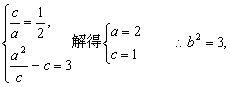
∴曲线E的标准方程为![]() 。
。
⑵设![]()
![]()
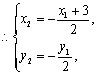
又∵A、B都在椭圆上,∴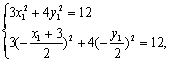
![]()
![]()
22.⑴以AB所在直线为x轴,线段AB的垂直平分线为y轴,建立直角坐标,并设点P坐标为P(x,y),设PA、PB分别切⊙O′于E、F,则PE=PF,AE=AC,BC=BF,
∵PA-PB=AC-BC=2![]() ,
,
故点P
的轨迹为以A、B为焦点,实轴长为2![]() 的双曲线右支(除去与
的双曲线右支(除去与![]() 轴交点)
轴交点)
由题意,![]() 故P点轨迹E的方程为:
故P点轨迹E的方程为:![]()
⑵设直线l的倾斜角为q,直线l方程为y =tanq·(x-2)及x=2,注意到q≠0,
∴直线![]() 方程可写成y·cotq=x-2,由直线l与E交于M、N两点知
方程可写成y·cotq=x-2,由直线l与E交于M、N两点知![]()
由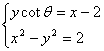
![]()
![]()
由y1-y22=![]() 得:S△AMN=
得:S△AMN=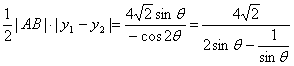
由![]() ,知
,知![]() ∵函数
∵函数![]() 在区间(0,-∞)上为增函数.
在区间(0,-∞)上为增函数.
∴![]() ,即
,即![]() 时,(S△AMN)min=4
时,(S△AMN)min=4![]()