高三单元试题之六不等式
(时量：120分钟 满分：150分)
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有
一项是符合题目要求的．
1．关于x的不等式x－1>m的解集为R的充要条件是 （ ）
A．m＜0 B．m≤－1 C．m≤0 D．m≤1
2．设0<b<a<1，则下列不等式成立的是 （ ）
A．ab<b2<1 B．a2<ab<1 C．2b<2a<2 D．
3．不等式组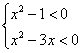
的解集是 （ ）
A．{x－1<x<1} B．{x0<x<3} C．{x0<x<1} D．{x－1<x<3}
4．设α，β，γ均为锐角，且
，则 （ ）
A．α<γ<β B．α<β<γ C．β<α<γ D．γ<α<β
5．已知函数f(x)=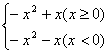
，则不等式f(x)+2>0的解区间是 （ ）
A．(－2，2) B．(－∞，－2)∪(2，＋∞)
C．(－1，1) D．(－∞，－1)∪(1，＋∞)
6．“a>1”是“
”的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
7．若a,b∈R，则使a+b>1成立的充分不必要条件是 （ ）
A．a+b≥1 B．b<－1 C．a≥1 D．
8．已知
,设M=
则M与N的大小关系是
（ ）
A．M>N B．M<N C．M=N D．不能确定
9．若
，
，则下列不等式恒成立的是 （ ）
A．
B．
C．
D．
10．某纯净水制造厂在净化水过程中，每增加一次过滤可减少水中杂质20%，要使水中杂质减少到原来的5%以下，则至少需过滤的次数为（参考数据lg2=0.3010,lg3=0.4771）（ ）
A. 5 B. 10 C. 14 D. 15
11．2
2—5—3＜0成立的一个必要不充分条件是 （ ）
A．—
B．—
C．—
D．—
12．若a>b，在①
；②a3>b3；③
；④
中，正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题：本大题共4小题，每小题4分，共16分．答案填在题中横线上．
13．已知点A（5，0）、B（5，4）、C（0，4），P是线段BC上的点，Q是线段AB上的点，
且∠POQ=45°，O为原点，则点P横坐标活动的范围是______。
14．观察下列式子：
，则可以猜想的结论为：_______
．
15．不等式
的解集是_______.
16．已知a,b均为实数，给出下列四个论断：
①a+b＝a+b；②a－b≤a+b；③
；④a+b>5。
以其中两个论断为条件，其余两个论断作为结论，写出一个正确的命题 。（用序号填写即可）
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
17．（本小题满分12分）若函数f(x)＝logax(其中a>0且a≠1)在x∈[2,+∞)上总有f(x)>1成立，求a的取值范围。
18．（本小题满分12分）已知实数
满足不等式
，试判断方程
有无实根，并给出证明．
19．（本小题满分12分）（1）已知
是正常数，
，
，求证：
，指出等号成立的条件；
（2）利用（1）的结论求函数
（
）的最小值，指出取最小值时的值．
20．（本小题满分12分）已知M是关于x的不等式2x2+(3a－7)x+3＋a－2a2<0解集，且M中的一个元素是0，求实数a的取值范围，并用a表示出该不等式的解集.
21．（本小题满分12分）已知二次函数f(x)的二次项系数为正且f(2－x)＝f(2＋x).
（理科）求不等式f(2－2ax2)<f(－ax2＋2ax－a＋2)的解集(a≠0).
（文科）求不等式
的解集.
22．（本小题满分14分）已知条件p：5x－1>a和条件
，请选取适当的实数a的值，分别利用所给的两个条件作为A、B构造命题：“若A则B”，并使得构造的原命题为真命题，而其逆命题为假命题.则这样的一个原命题可以是什么？并说明为什么这一命题是符合要求的命题.
高三单元试题之六：不等式参考答案
一、1．A 2．C 3．C 4．A 5．A 6．A 7．B 8．A 9．A 10．C 11．D 12．B
二、13．[
14．
15．{x0≤x≤4}16．①③
②④
三、17．解：a>1时，f(x)＝logax为增函数，当x∈[2,+∞)时，f(x)有最小值 f(2)＝loga2；
0<a<1时f(x)＝logax为减函数，当x∈[2,+∞)时，f(x)有最大值 f(2)＝loga2；
∵f(x)在x∈[2,+∞)上总有f(x)>1成立，
∴a>1时loga2>1loga2>11<a<2；0<a<1时loga2>1loga2<－1
<a<1。
∴1<a<2或
。
18．由
，解得
，∴
，∴
.
∴方程z2－2z+5－p2=0的判别式△＝4(p2－4)<0，
从而方程z2－2z+5－p2=0无实根.
19．⑴
，
故．当且仅当
，即
时上式取等号；
⑵由⑴
．
当且仅当
，即
时上式取最小值，即
．
20．原不等式即(2x－a－1)(x＋2a－3)<0，
由
适合不等式故得
，所以
，或
.
若，则
，∴
，
此时不等式的解集是
；
若，由
，∴
，
此时不等式的解集是
。
21．解：（理）∵f(2－x)=f(2+x)，∴f(x)的对称轴为x=2，
又∵f(x)的二次项系数大于零，∴f(x)在(－∞，2]上是减函数，在[2，+∞)上是增函数。
⑴当a>0时，2－2ax2≤2，－ax2+2ax－a+2＝－a(x－1)2+2≤2，依题意得
2－2ax2>－ax2+2ax－a+2
ax2+2ax－a<0x2+2x－1<0，解得
⑵当a<0时，2－2ax2≥2，－ax2+2ax－a+2＝－a(x－1)2+2≥2，依题意得
2－2ax2<－ax2+2ax－a+2ax2+2ax－a>0x2+2x－1<0，解得
综上所述：原不等式的解集为
。
解：(文) ∵f(2－x)=f(2+x)，∴f(x)的对称轴为x=2，
又∵f(x)的二次项系数大于零，∴f(x)在(－∞，2]上是减函数，
又∵2－
x2≤2，－x2+6x－7＝－(x－3)2+2≤2，∴2－x2>－x2+6x－7，
即x2－12x+18>0，解得
。
故原不等式的解集为：
。
22．分析：本题为一开放性命题，由于能得到的答案不唯一，使得本题的求解没有固定的模式，学生既能在一般性的推导中找到一个满足条件的
，也能先猜后证，所找到的实数只需满足
，且
1即可.这种新颖的命题形式有较强的综合性，同时也是对于四个命题考查的一种新尝试，如此命题可以考查学生探究问题、解决问题的能力，符合当今倡导研究性学习的教学方向.
解：已知条件即
，或
，∴
，或
，
已知条件
即
，∴
，或
；
令
，则即
，或，此时必有
成立，反之不然.
故可以选取的一个实数是，A为，B为，对应的命题是若则，
由以上过程可知这一命题的原命题为真命题，但它的逆命题为假命题.