高三单元试题之七直线和圆的方程
一、 选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
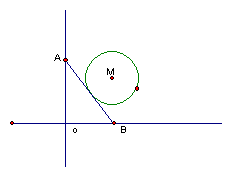
1. 设集合M={直线},P={圆},则集合M∩P中的元素个数为 ( )
A.0 B.1 C.2 D.0或1或2
2. 直线l经过A(2,1)、B(1,m2)(m∈R)两点,那么直线l的倾斜角的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 过点M(2,1)的直线与x轴交于P点,与y轴交于Q点,且MP=MQ,则此直线的方程是( )
A.x-2y+3=0 B.2x-y-3=0 C.2x+y-5=0 D.x+2y-4=0
4.
已知点A(6,-4),B(1,2)、C(x,y),O为坐标原点。若![]() 则点C的轨迹方程是( )
则点C的轨迹方程是( )
A.2x-y+16=0 B.2x-y-16=0 C.x-y+10=0 D.x-y-10=0
5. 设动点P在直线x=1上,O为坐标原点,以OP为直角边,点O为直角顶点作等腰Rt△OPQ,则动点Q的轨迹是( )
A.圆 B.两条平行直线 C.抛物线 D.双曲线
6.
已知实数x、y满足x2+y2=4,则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7. 若点(5,b)在两条平行直线6x-8y+1=0与3x-4y+5=0之间,则整数b的值为( )
A.5 B.-5 C.4 D.-4
8.不等式组![]() 表示的平面区域是 ( )
表示的平面区域是 ( )
A.矩形 B.三角形 C.直角梯形 D.等腰梯形
9.4个茶杯和5包茶叶的价格之和小于22元![]() ,而6个茶杯与3包茶叶的价格之和大于24
,而6个茶杯与3包茶叶的价格之和大于24
元,则2个茶杯与3包茶叶的价格比较 ( )
A. 2个茶杯贵 B.3包茶叶贵 C.二者相同 D.无法确定
10.直线l的倾斜角是α,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.直线ax+by+b-a=0与圆x2+y2-x-2=0的位置关系是 ( )
A.相离 B.相交 C.相切 D.与a,b的取值有关
12.在圆x2+y2=5x内,过点![]() 有n条弦的长度成等差数列,最小弦长为数列的首项a1,最大弦长为an,若公差
有n条弦的长度成等差数列,最小弦长为数列的首项a1,最大弦长为an,若公差![]() ,那么n的取值集合为
( )
,那么n的取值集合为
( )
A.{4,5,6,7} B.{4,5,6} C.{3,4,5,6} D. {3,4,5}
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
13.圆心在直线2x+y=0上,且与直线x+y-1=0切于点(2,-1)的圆的方程是 。
14.将直线y=-![]() x+2
x+2![]() 绕点(2,0)按顺时针方向旋转30°所得直线方程是
。
绕点(2,0)按顺时针方向旋转30°所得直线方程是
。
15.在坐标平面内,由不等式组![]() 所确定的平面区域的面积为
.
所确定的平面区域的面积为
.
16.已知定点P(2,1),分别在y=x及x轴上各取一点B与C,使![]() BPC的周长最小,最小值为__________ .
BPC的周长最小,最小值为__________ .
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.某工厂的一个车间生产某种产品,其成本为每公斤27元,售价为每公斤50元。在生产产品的同时,每公斤产品产生出0.3立方米的污水,污水有两种排放方式:其一是输送到污水处理厂,经处理(假设污水处理率为85%)后排入河流;其二是直接排入河流.若污水处理厂每小时最大处理能力是0.9立方米污水,处理成本是每立方米污水5元;环保部门对排入河流的污水收费标准是每立方米污水17.6元,根据环保要求该车间每小时最多允许排入河流中的污水是0.225立方米.试问:该车间应选择怎样的生产与排污方案,才能使其净收益最大.
18.圆的方程为x2+y2-6x-8y=0,过坐标原点作长为8的弦,求弦所在的直线方程。
19.已知定点A(0,1),B(0,-1),C(1,0)。动点P满足:![]() 。
。
⑴求动点P的轨迹方程,并说明方程表示的曲线;
⑵当![]() 的最大值和最小值。
的最大值和最小值。
20.已知圆M:2x2+2y2-8x-8y-1=0和直线l:x+y-9=0过直线 上一点A作△ABC,使∠BAC=45°,AB过圆心M,且B,C在圆M上。
⑴当A的横坐标为4时,求直线AC的方程;
⑵求点A的横坐标的取值范围。
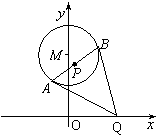 21.如图,已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点,
21.如图,已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点,
⑴如果![]() ,求直线MQ的方程;
,求直线MQ的方程;
⑵求动弦AB的中点P的轨迹方程.
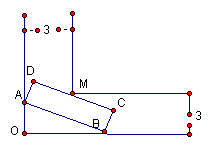
22.某建筑物内一个水平直角型过道如图所示,两过道的宽度均为3米,有一个水平截面为矩形的设备需要水平移进直角型过道,若该设备水平截面矩形的宽为1米,长为7米. 问:该设备能否水平移进拐角过道?
高三单元试题之七:直线和圆的方程参考答案
一、1.B 2.B 3.D 4.B 5.B 6.A 7.C 8.B 9.A 10.A 11.B 12.A
二、13.(x-1)2+(y+2)2=2 14.x=2 15.16 16.![]()
三、17.解:设该车间每小时净收益为z元,生产的产品为每小时x公斤,直接排入河流的污水量为每小时y立方米。则该车间每小时产生污水量为0.3x; 污水处理厂污水排放量为0.3x-y,经污水处理厂处理后的污水排放量为(1-0.85)(0.3 x-y),车间产品成本为27x,车间收入为50x,车间应交纳排污费用17.6[(1-0.85)(0.3 x-y)+y],车间应交纳污水处理费5(0.3x-y),于是z=50x-27x-5(0.3x-y)-17.6[0.15 (0.3x-y)+y]=20.708x-9.96y.
|
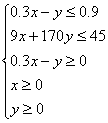
故该车间应每小时生产3.3公斤产品,直接排入河流的污水量为每小时0.09立方米,这样净收益最大.
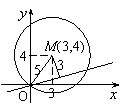 18.解:x2+y2-6x-8y=0即(x-3)2+(y-4)2=25,设所求直线为y=kx。
18.解:x2+y2-6x-8y=0即(x-3)2+(y-4)2=25,设所求直线为y=kx。
∵圆半径为5,圆心M(3,4)到该直线距离为3,
∴ ![]() ,
,
∴![]() ,∴
,∴![]() 。 ∴所求直线为
。 ∴所求直线为![]() 或
或![]() 。
。
19.解:⑴设动点的坐标为P(x,y),则![]() =(x,y-1),
=(x,y-1),![]() =(x,y+1),
=(x,y+1),![]() =(1-x,-y)
=(1-x,-y)
∵![]() ·
·![]() =k
=k![]() 2,∴x2+y2-1=k[(x-1)2+y2]即(1-k)x2+(1-k)y2+2kx-k-1=0。
2,∴x2+y2-1=k[(x-1)2+y2]即(1-k)x2+(1-k)y2+2kx-k-1=0。
若k=1,则方程为x=1,表示过点(1,0)是平行于y轴的直线。
若k≠1,则方程化为:![]() ,表示以(
,表示以(![]() ,0)为圆心,以
,0)为圆心,以![]() 为半径的圆。
为半径的圆。
⑵当k=2时,方程化为(x-2)2+y2=1。∵2![]() +
+![]() =2(x,y-1)+(x,y+1)=(3x,3y-1),
=2(x,y-1)+(x,y+1)=(3x,3y-1),
∴2![]() +
+![]() =
=![]() 。又x2+y2=4x-3,∴2
。又x2+y2=4x-3,∴2![]() +
+![]() =
=![]() ∵(x-2)2+y2=1,∴令x=2+cosθ,y=sinθ。
∵(x-2)2+y2=1,∴令x=2+cosθ,y=sinθ。
则36x-6y-26=36cosθ-6sinθ+46=6![]() cos(θ+φ)+46∈[46-6
cos(θ+φ)+46∈[46-6![]() ,46+6
,46+6![]() ],
],
∴2![]() +
+![]() max=
max=![]() =3+
=3+![]() ,2
,2![]() +
+![]() min=
min=![]() =
=![]() -3。
-3。
20.解:⑴依题意M(2,2),A(4,5),![]() ,设直线AC的斜率为
,设直线AC的斜率为![]() ,则
,则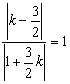 ,解得
,解得![]() 或
或![]() ,故所求直线AC的方程为5x+y-25=0或x-5y+21=0;
,故所求直线AC的方程为5x+y-25=0或x-5y+21=0;
⑵圆的方程可化为(x-2)2+(y-2)2=![]() ,设A点的横坐标为a。则纵坐标为9-a;
,设A点的横坐标为a。则纵坐标为9-a;
①当a≠2时,![]() ,设AC的斜率为k,把∠BAC看作AB到AC的角,则可得
,设AC的斜率为k,把∠BAC看作AB到AC的角,则可得![]() ,直线AC的方程为y-(9-a)=
,直线AC的方程为y-(9-a)=![]() (x-a)即5x-(2a-9)y-2a2+22a-81=0,又点C在圆M上,所以只需圆心到AC的距离小于等于圆的半径,即
(x-a)即5x-(2a-9)y-2a2+22a-81=0,又点C在圆M上,所以只需圆心到AC的距离小于等于圆的半径,即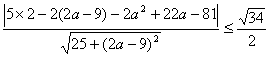 ,化简得a2-9a+18≤0,解得3≤a≤6;
,化简得a2-9a+18≤0,解得3≤a≤6;
②当a=2时,则A(2,7)与直线 x=2成45°角的直线为y-7=x-2即x-y+5=0,M到它的距离![]() ,这样点C不在圆M上,还有x+y-9=0,显然也不满足条件,故A点的横坐标范围为[3,6]。
,这样点C不在圆M上,还有x+y-9=0,显然也不满足条件,故A点的横坐标范围为[3,6]。
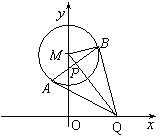 21.解:⑴解(1)由
21.解:⑴解(1)由![]() 可得
可得![]() 由射影定理得
由射影定理得![]() 在Rt△MOQ中,
在Rt△MOQ中,
![]() ,
,
故![]() ,所以直线AB方程是
,所以直线AB方程是
![]()
⑵连接MB,MQ,设![]() 由点M,P,Q在一直线上,得
由点M,P,Q在一直线上,得![]()
由射影定理得![]() 即
即![]()
把(A)及(B)消去a,并注意到![]() ,可得
,可得![]()
22.解:由题设,我们以直线OB,OA分别为x轴,y轴建立直角坐标系,问题可转化为:求以M(3,3)点为圆心,半径为1的圆的切线被x的正半轴和y的正半轴所截的线段 AB长的最小值。设直线AB的方程为![]() ,∵它与圆
,∵它与圆![]() 相切,
相切,
∴ ![]() ……(1) ,又∵原点O(0,0)与点M(3,3)在直线
……(1) ,又∵原点O(0,0)与点M(3,3)在直线![]() 的异侧,∴
的异侧,∴![]() ,∴(1)式可化为
,∴(1)式可化为![]() ……(2)
……(2)
下面求![]() (a>0,b>0)的最小值。设
(a>0,b>0)的最小值。设
![]() 代入(2)得
代入(2)得![]() ,……(3)
,……(3)
再设t=sinθ+cosθ,![]() .
.![]() ,代入(3)
,代入(3)
得![]() ,
,![]() ,记
,记![]()
这里f(1)=-4<0, ![]() 在
在![]() 内有解
内有解![]()
![]() 。这时
。这时![]()
|
故该设备不能水平移进过道。
另解:![]()
∴r(t) 在![]() 上是减函数,
上是减函数,![]() 。
。