泸州市高中2006级第一次诊断考试
数 学（文史财经类）
本试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷第1至2页，第Ⅱ卷第3至8页。120分钟完卷，满分150分。
第Ⅰ卷（选择题，共60分）
注意事项：
1. 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2. 每小题选出答案后，用铅笔把答题卡 上对应题目的答案标号涂黑，若需改动，用橡皮擦擦干净后，再选涂其它答案，不准答在本题单上。
参考公式：
如果事件A、B互斥，那么P(A+B)=P(A)+P(B)；
如果事件A、B相互独立，那么P(A•B)=P(A)•P(B)；
如果事件A在一次试验中发生的概率为P，那么n次独立重复试验中恰好发生k次概率：
。
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的，把它选出来填涂在答题卡上。
（1）已知集合
，
，则集合B中的元素个数为
A. 2 B. 3 C. 4 D. 5
（2）与函数y=x相同的是
A. 
B.
C. 
D.
（3）函数
的最小正周期是
A. 
B. 
C.4
D. 1
（4）函数
的反函数是
A. 
B.
C. 
D.
（5）函数
的一个单调递减区间是
A. 
B. 
C. 
D. 
（6）设A(1，2)，B(4，2)，若点A、B按向量
平移后对应点
，则
=
A. （2，3） B.（3，5） C.（3，0） D. （－4，3）
（7）等比数列
的前n项和为Sn，已知S4=1，S8=3，则
的值为
A. 32 B. 16 C. 8 D. 4
（8）已知单位向量a、b，它们的夹角为
，则
的值为
A. 
B.
－10
C. 10
D. 
（9）已知函数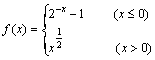
，若
，则x0的取值范围是
A. （－1，1）
B. (
)
C. 
D.
（10）在ΔABC中，角A、B、C所对边分别是a、b、c，且
，则ΔABC的形状是
A. 等腰三角形或直角三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰三角形
（11）定义在R上的偶数函数
在
上是增函数，若
，则适合不等式
>0的x的取值范围是
A. 
B.
C.
D. 
（12）甲、乙两工厂2004年元月份的产值相等，甲厂的产值逐月增加且每月增加的数量相同，乙厂产值也逐月增加且每月的增长率相同，若2005年元月份两厂的产值又相等，则2004年7月份两厂的产值关系是
A. 甲厂的产值高 B. 乙厂的产值高
C. 甲厂、乙厂的产值相同 D. 无法确定
泸州市高中2006级第一次诊断考试
数 学（文史财经类）
第Ⅱ卷（非选择题 共90分）
注意事项：(1)用钢笔或圆珠笔直接答在试题卷上。(2)答题前请将密封线内的项目填写清楚。
| 题号 | 二 | 三 | 总分 | |||||
| （17） | （18） | （19） | （20） | （21） | （22） | |||
| 分数 | ||||||||
| 得分 |
| ||
|
|
（13）一个容量为20的样本，数据的分组及各组的频数如下：
(10，20]，2；（20，30]，3；（30，40]，4；（40，50]，5；（50，60]，4；（60，70]，2。
则样本在区间(10，50]上的频率为 。
（14）已知向量
与
共线，则实数n=
。
（15）设数列的前n项和Sn满足：
，则该数列的通项公式an= 。
（16）给出以下命题
①设
，则
；②函数
的图象的一条对称轴为
；③要得到函数
的图象只须将
的图象向左平移个单位长度。其中正确命题的序号是
。
| 得分 |
| ||
|
|
（17）（本小题满分12分）
若A是锐角，向量
且
。
求tan2A的值。
| 得分 |
| ||
|
|
已知
，若
，求实数a的范围。
| 得分 |
| ||
|
|
函数
在[0，2]上的最大值为
，求实数a的值与函数f(x)取得最大值时的x集合。
| 得分 |
| ||
|
|
2005年10月27日第十届全国人大常委第十八次会议通过了关于修改《中华人民共和国个人所得税法》的决定，修改后的《中华人民共和国个人所得税法》规定“个人工资、薪金等所得，以每月收入额减除费用一千六百元后的余额，为应纳税所得额。”修改后的个人所得率税率表为：
| 级数 | 全月应纳税所得额 | 税率% |
| 1 | 不超过500元的 | 5 |
| 2 | 超过500元至2000元的部份 | 10 |
| 3 | 超过2000元至5000元的部份 | 15 |
| 4 | 超过5000元至20000元的部份 | 20 |
| … | … |
（1）设个人的月工资、薪金等所得为x元（
），月纳税额为y元，写出y与x的函数关系式；
（2）若某职员某月工资、薪金等所得为3300元，求该职员该月应纳税多少元？
| 得分 |
| ||
|
|
已知函数
在x=2时有极值，其图象在点（1，f(1)）处的切线与直线
平行。
（1）求该函数的单调递减区间；
（2）当m>0时，求函数f(x)在[0,m]上的最小值。
| 得分 |
| ||
|
|
设等差数的前n项和为Sn，公差d >0，若
。
（1）求数列的通项公式；
（2）设
，若
是等差数列，求实数a的值；
（3）在（1）（2）下，设
。是否存在正整数m、n，使
成立，若存在，求出m、n的值；若不存在，说明理由。