高三数学期末综合练习(八)
一、选择题:(本大题12个小题,每小题5分,共60分)各题答案必需答在答题卡上。
1.不等式 ![]() 的解集为
( )
的解集为
( )
(A)(一2.1) (B)(一1,2) (C)(一∞,一2) ∪(1,+∞) (D)(一∞,一1)∪(2,+∞)
2.不等式x(1-3x)>0的解集是 ( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
3函数y=2x+1(-1≤x<0)的反函数是 ( )
A.y=1+log2x(x>0) B.y=-1+log2x(x>0)C.y=1+log2x(1≤x<2)D.y=-1+log2x(1≤x<2)
4设向量确![]() = (3,一3),
= (3,一3),![]() = (一5,一1),则
= (一5,一1),则 ![]() 等于 ( )
等于 ( )
(A)(一2, 4) (B)(—1,一2) (C)(4.一1) (D)(一4,1)
5设等比数列{an}的首项为a1,公比为q,则“a1<O,且0<q<1”是“对于任意正整数n,都有 an+1>an”的 ( )
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D)既不充分也不必要条件
6设l1 、l2为两条直线,a、β为两个平面,给出下列四个命题:
(1)若l1![]() , l2
, l2![]() ,l1∥β,l1∥a则a∥β. (2)若l1⊥a ,l2⊥a,则l1∥l2
,l1∥β,l1∥a则a∥β. (2)若l1⊥a ,l2⊥a,则l1∥l2
(3)若l1∥a,l1∥l2,则l2∥a (4)若a⊥β,l1![]() ,,则l1⊥β
,,则l1⊥β
其中,正确命题的个数是 ( )
(A)0个 (B)1个 (C)2个 (D)3个
7设函数,![]() 若对任意x∈R,都有,f (x1 )≤f (x )≤f (x2 )成立,则x1 —x2的最小值为
( )
若对任意x∈R,都有,f (x1 )≤f (x )≤f (x2 )成立,则x1 —x2的最小值为
( )
(A)4 (B)2
(C)1 (D) ![]()
![]() x—y≥O
x—y≥O
8.已知x , y∈Z.则满足 x+y≤5 的点(x ,y)的个数为 ( )
y≥o
(A) 9 (B)10 (C) 11 (D)12
9已知函数,![]() (m为常数)图像上点A处的切线与直线2一y+3=0的夹角为45o。则点A的横坐标为
( )
(m为常数)图像上点A处的切线与直线2一y+3=0的夹角为45o。则点A的横坐标为
( )
(A) 0 (B) 1 (C) 0或![]() (D) l或
(D) l或![]()
1O.设双曲线16x2—9y 22 = 144的右焦点为F2,M是双曲线上任意一点 , 点A的坐标为
(9,2).则 MA+![]() MF2 的最小值为 ( )
MF2 的最小值为 ( )
(A) 9
(B) ![]() (C)
(C)
![]() (D)
(D) ![]()
11. a, b是异面直线,A、B∈a, C、D∈b,AC⊥b,BD⊥b,且AB=2,CD=1,则a与b所成的角为 ( )
A.30° B.60° C.90° D.45°
12.设奇函数f (x )在[—1,1]上是增函数,且f (—1)= 一1.若函数,,f (x ) ≤ t 2一2 a t +l对所有的 x∈[一1.1]都成立,则当a∈[1,1]时,t 的取值范围是 ( )
(A)一2≤t≤2 (B)
![]() ≤t≤
≤t≤![]()
(C) t≥2或t≤一2或t = 0
(D) t≥![]() 或t≤
或t≤![]() 或t=0。
或t=0。
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中的横线上.
13.若球的大圆面积为3π,则该球的体积为 .
14.若向量![]() 的夹角为
的夹角为![]() ,
,![]() ,则
,则![]() .
.
15.同学们都知道,在一次考试后,如果按顺序去掉一些高分,那么班级的平均分将降低;
反之,如果按顺序去掉一些低分,那么班级的平均分将提高. 这两个事实可以用数学语
言描述为:若有限数列![]() 满足
满足![]() ,则
,则
(结论用数学式子表示).
16.若二次函数f 1 (x ) 、 f 2(x ) 满足条件:f (x )= f 1 (x )+ f 2 (x )在(一∞,+∞)上单调递增,(2)g= f1 (x ) — f2 (x )对任意实数 x1 、x2 (x1 ≠x2)都有![]() ,则f 1 (x ) =
,f 2 (x )= 。(只须填上你认为正确的一组即可)
,则f 1 (x ) =
,f 2 (x )= 。(只须填上你认为正确的一组即可)
高三数学期末综合练习(八)
班级 姓名 学号 得分
一. 选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二. 填空题(每小题4分,共16分)
13. ; 14. ;
15. ; 16. ;
三、解答题:(本大题6个小题,共74分)各题解答必需答在答题卡Ⅱ上(必需写出必要
的文字说明、推理过程或计算步骤)。
17.(本小题满分12分)
已知![]() =(cos2a,slna);
=(cos2a,slna);![]() = (1,2sina—1),a∈(
= (1,2sina—1),a∈(![]() , π),
, π),![]() ·
·![]() =
=![]() ,求cos(a+
,求cos(a+![]() )是值
)是值
18(本小题满分12分)
已知p:f -1 (x )是,f (x )=1—3x的反函数,且 f -1 (a ) <2
p:集合A = { x x 2 +( a+2) x +l = 0,x∈R},B = { x x >0},且A∩B=φ
求实数a的取值范围,使p、q中有且只有一个为真命题
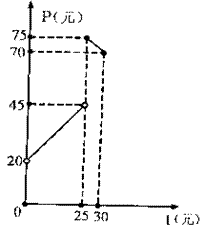 19(本小题满分12分)
19(本小题满分12分)
某种商品在30天内每件的销售价格P(元)与时问t(天)的函数关系用右图的两条线段表示:
该商品在30天内日销售量Q (件)与时问t (天)之间的关系如下表所示:
(I)根据提供的图像,写出该商品每件的销售价格P与时间t的函数关系式
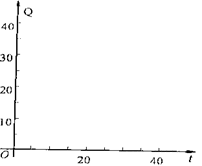 (Ⅱ)在所给直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数关系式
(Ⅱ)在所给直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数关系式
(Ⅲ)求该商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?(日销售金额一每件的销售价格×日销售量)
20(本小题满分12分)
如图,正三角形ABC的边长为2,D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠,使A、B、C三点重合,构成三棱锥A— DEF 。
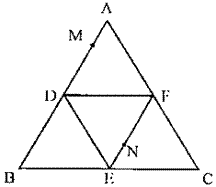 (I)求平面ADE与底面DEF所成二面角的余弦值
(I)求平面ADE与底面DEF所成二面角的余弦值
(Ⅱ)设点M、N分别在AD、EF上,![]() (λ>O,λ为变量)
(λ>O,λ为变量)
①当λ为何值时,MN为异面直线AD与EF的公垂线段?
请证明你的结论
②设异面直线MN与AE所成的角为a,异面直线MN与DF所成的角为β,试求a+β 的值
21(本小题满分12分)
已知函数,![]() ,数列{an }满足
,数列{an }满足![]()
(I)求数列{an }的通项公式 (Ⅱ)记Tn =![]()
①求Tn ;②设数列{bn }的通项公式为![]() .求证:bn·Tn≤20
.求证:bn·Tn≤20
(符号“∑”表示将若干个数相加如,x1 + x2 +…+ xn 记作![]() )
)
22. (本小题满分14分)
椭圆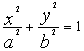 (a > b>0)的两个焦点为F1 (—c,0)、F2(c,0),M是椭圆上一点,满足
(a > b>0)的两个焦点为F1 (—c,0)、F2(c,0),M是椭圆上一点,满足![]() ;(I)求离心率e的取值范围
;(I)求离心率e的取值范围
(Ⅱ)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为![]()
(1)求此时椭圆G的方程;
(2)设斜率为k (k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为A、B的中点,问:A、B两点能否关于过点![]() 、Q的直线对称? 若能,求出^的取值范围;若不能,请说明理由
、Q的直线对称? 若能,求出^的取值范围;若不能,请说明理由
高三数学期末综合练习(八)
参考答案及评分标准
l.C 2.D 3.D 4.D 5.A 6.B 7.B 8. D 9.C 10.B 11.B 12.C
二.13.![]() 14.2 ;
14.2 ;
15.![]() 和
和
![]()
16.如:f 1 (x1 )= —x2 + x f 1 (x) = —x + x
三、解答题
17.![]() ·
·![]() =cos2a+sin(2sina
—1)=2cos2a一1+2sin2a一sina=1—sina
5分 由
=cos2a+sin(2sina
—1)=2cos2a一1+2sin2a一sina=1—sina
5分 由![]() ,
,![]() 7分
7分 ![]() ∴
∴![]() 9分
9分
∴ ![]() 12分
12分
18:∴f 1 (x)=1 —3 x ∴![]() 1分
1分
由![]() 3分
3分
当△<0时A≠φ,此时(a+2)2一4<0,一4<a<05分 当△≥。时,由A∩B=φ
![]() 得 △=(a+2)2一4≥0
得 △=(a+2)2一4≥0
x1一x2= 一(a+2) <0 解得a≥0。 7分 由此得a<0,a>一4 8分 (1)要使p真q假,则
![]()
![]() —5<a<7
a≤—5或
a ≥7
—5<a<7
a≤—5或
a ≥7
解得一5<a≤一4 10分(2)要使p假q真, 则 解得a ≥7 11分
a≤—4, a>一4
∴当4的取值范围是(5,一4]∪[7.+∞)时.p、q中有且只有一个为真命题 1 2分
19解:(1)根据图像,每件的销售价格P与时间t的函数关系式为;
![]() t +20, (0<t<25
t∈N’)
t +20, (0<t<25
t∈N’)
P=
一t+100, (25≤t≤30, t∈N’)3分
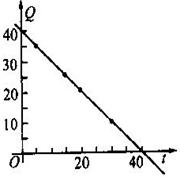 (2)描出实数对(t.Q)的对应点如图所示4分
(2)描出实数对(t.Q)的对应点如图所示4分
从图像发现:点(5,35),(15,25),(20.20),(30.10)似乎在同一条直线上,为此假设它们共线于直线l,Q=kt+b. 5分
由点(5,35).(30,10)确定出l的解析式为Q=t+40 通过检验可知.点(15,25).(20.20)也在直线l上。
∴日销售量Q与时间t的一个函数关系式为Q= 一t+40,(O<t≤3,·t∈N’)
(3)设日销售金额为y(元)
![]()
![]() —t+20t+800,(0<t<25,t∈N’)
—(t—10)2+900 , (0<t<25,t∈N’)
—t+20t+800,(0<t<25,t∈N’)
—(t—10)2+900 , (0<t<25,t∈N’)
则y= =
t2—140t+4000 (25≤t≤30 ,t∈N’) (t—70)2+900, (25≤t≤30 ,t∈N’)
9分 若0<t<25(t∈N’),则当t=10时,ymat=900 10分
若25≤t≤30(t∈N·),则当t=25时,ymat=1125,11分由1125>900,知ymat=1125。
∴这种商品日销售金额的最大值为1125元,30天中的第25天的日销售金额最大。 12分
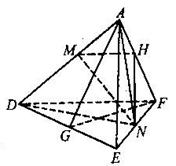 20。解法一:
20。解法一:
(Ⅰ)如图,取DE的中点G,连接AG、FG 1分
由题意AD=AE,△DEF为正三角形,得AG⊥DE,
∴∠AGF为平面ADE与底面DEF所成二面角的平面角。2分
由题意得AG=FG=![]() 。在△AGF中,
。在△AGF中,
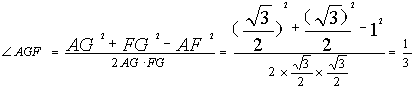 ∴平面ADF与底面DEF所成二面角的余弦值为
∴平面ADF与底面DEF所成二面角的余弦值为![]() 4分
4分
(Ⅱ)(1)λ=1时,MN为异面直线AD与EF公垂线段 5分
当λ=1,M为AD的中点,N为FF的中点,连结AN、DN,
则由题意,知AN=DN=![]() ,∴MN⊥AD,同理可证MN⊥EF 7分 ∴λ=1时,MN为异面直线AD与EF公垂线段。
,∴MN⊥AD,同理可证MN⊥EF 7分 ∴λ=1时,MN为异面直线AD与EF公垂线段。
(2)过点M作MH∥DF,交AF于点H,则∠HMN为异面直线 MN与DF所成的角 。 8分
由MH∥DF,得 ![]() ,∴
,∴![]()
∴HN//AE,∠MNH为异面直线 MN与AE所成的角 。 9分
∴α+β=∠MNH+∠HMN=π—∠MHN 10分
由题意得,三棱锤A—DEF是正棱锤,则点A在底面DEF上的射影为底面△DEF的中心,记为O。
∵ AE在底面DEF上的射影EO⊥DF, ∴AE⊥DF11分。
 又∵HN//AE,MH//DF,∴∠MNH=
又∵HN//AE,MH//DF,∴∠MNH=![]() ,∴
,∴![]() 12分
12分
解法二:
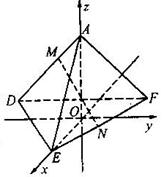
同解法一,另解如下:由题意三棱锤A—DEF是正棱锤,点A在底面DEF上的射影为正三角形DEF的中心,记为O,则![]() 1分
1分
以点O为原点,OE所在直线为x ,在平面DEF内过点O与OE垂直的直线为y,
则得O(0,0,0),
![]()
由题意.易知三角形ADE的中心p的坐标为![]() 。则平面ADE的法向量
。则平面ADE的法向量![]() 3分
3分
平面DEF的法向量![]() 所成的角θ平面ADF与底面DEF所成二面角的平面角,
所成的角θ平面ADF与底面DEF所成二面角的平面角,
又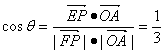
∴平面ADF与底面DEF所成二面角的余弦值为 ![]() 4分
4分
(Ⅱ)(1)λ=1时,MN为异面直线AD与EF的公垂线段 5分当λ=1时,M为AD的中点,N为EF的中点。此时点M的坐标为![]() .点N的坐标
.点N的坐标![]() ,
,
∴![]()
∴![]()
∴![]() ,即MN⊥AD 同理可证MN⊥EF
7分
,即MN⊥AD 同理可证MN⊥EF
7分
∴λ=1时,MN为异面直线AD与EF的垂线段
(2)
![]()
又![]() ,∴
,∴![]()
∴![]() 又∵0<a+β<π
∴a+β=
又∵0<a+β<π
∴a+β=![]() 12分
12分
21.解:(Ⅰ)∵f (x)=![]() ,∴
,∴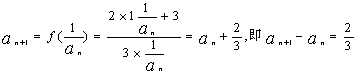
∴数列{an}为等差散列,![]() 。3分
。3分
(Ⅱ)(1)
![]()
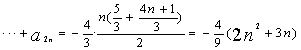 。 6分
。 6分
(2)![]() 7分
7分
设![]() 8分
8分
![]() 9分
9分
∵![]() ∴g(x)在(0,5
] 单调递减,在[6,+∞) 单调递减增 10分
∴g(x)在(0,5
] 单调递减,在[6,+∞) 单调递减增 10分
∴b1 T1<b2 T2<…<bn Tn bn Tn>b1 T1>bk Tk … 11分 又![]() ∴
∴![]() 12分
12分
22解:(I)设点M的坐标为(x,y),则![]() =(x+c· y),
=(x+c· y),![]() =(x-c· y)由
=(x-c· y)由![]() ·
·![]() =0得
=0得![]() ① 1分 又由点M在椭圆上得
① 1分 又由点M在椭圆上得![]() , 2分
, 2分
∵ 0≤x≤![]() ∴0≤
∴0≤![]() ,
,![]() l , 解得
l , 解得![]()
又∵0≤e≤1
, ∴![]() ,
,
(Ⅱ)(1)当离心率e取最小值![]() 时.椭圆方程可表示
时.椭圆方程可表示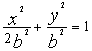 ,
1分
,
1分
设点H(x,y)是椭圆上的一点,则 HN2= x2+(y —3) 2=(2 b 2一2 y 2)+( y一3) 2= -(y+3) 2
+2 b 2+1 8(一b≤y≤b) 6分 (1)若0< b <3则一b>一3.
当,y= 一6时,HN2有最大值b 2+6 b +9=50
由题意知:b 2+6 b +9=50,![]() ,这与o<b<3矛盾 8分
,这与o<b<3矛盾 8分
(2)若b≥3.则一b≤3,
当y= —3,时HN2有最大值2 b 2+18
由题意知:2 b 2+18=50·b 2=l 6 .
∴所求椭圆方程为![]() 8分
8分
(2)设直线l的方程为y=kx+m,代人![]() 中,得(1+k2) x2+4 kxm +(2m2—
中,得(1+k2) x2+4 kxm +(2m2—
32)=0 9分
由直线l与椭圆G相交于不同的两点知△=(4km )2一4(1+2k2)(2m2—32)>0 。
∴ m2<32 k2+16 ②10分 要使A、B两点关于过点P、Q的直线对称,必须![]() 设A(x1 , y1)、B(x2 , y2),
设A(x1 , y1)、B(x2 , y2),
则![]()
∵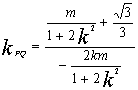 ∴
∴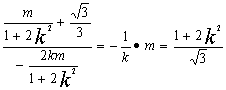 ③ 13分
③ 13分
由②、③得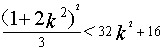 , ∴
, ∴![]() 12分
12分
又∵k≠0
∴![]() 时,AB两点关于过点P、Q对称。
14分
时,AB两点关于过点P、Q对称。
14分