高三数学期末综合练习(七)
一、选择题:(本大题12个小题,每小题5分,共60分)各题答案必需答在答题卡上。
1.cos600°= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知函数![]() = ( )
= ( )
A.b B.-b C.![]() D.-
D.-![]()
|
4.一元二次方程![]() 有一个正实数根和一个负实数根的充分不必要条件
有一个正实数根和一个负实数根的充分不必要条件
是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若![]() ,则下列不等式成立的是( )
,则下列不等式成立的是( )
(A)![]() . (B)
. (B)![]() . (C)
. (C)![]() .(D)
.(D)![]() .
.
6.已知平面![]() 、
、![]() 都垂直于平面
都垂直于平面![]() ,且
,且![]() 给出下列四个命题:
给出下列四个命题:
①若![]() ;②若
;②若![]() ;③若
;③若![]() ;④若
;④若![]() .
.
其中真命题的个数为 ( )
A.4 B.3 C.2 D.1
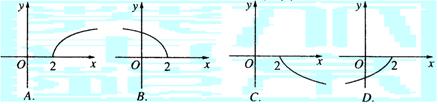
7.若把函数![]() 的图象按向量
的图象按向量![]() 平移后,得到函数
平移后,得到函数![]() 的图象,则原图象的函数解析式可以为 ( )
的图象,则原图象的函数解析式可以为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.已知奇函数![]() 的定义域为
的定义域为![]() ,且对任意正实数
,且对任意正实数![]() ,恒有
,恒有 ![]() ,则一定有 ( )
,则一定有 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.已知平面上直线l的方向向量e=![]() ,点O(0,0)和A(1,-2)在l上的射影分别是O1和A1,则
,点O(0,0)和A(1,-2)在l上的射影分别是O1和A1,则![]() ,其中λ= ( )
,其中λ= ( )
A.![]() B.-
B.-![]() C.2 D. -2
C.2 D. -2
10.若双曲线![]() 和椭圆
和椭圆![]() 的离心率互为倒数,那么以a,b,m为边长的三角形是 ( )
的离心率互为倒数,那么以a,b,m为边长的三角形是 ( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
11.若正四面体的四个顶点都在一个球面上,且正四面体的高为4,则该球的体积为( )
|
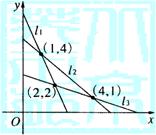
12.某城市各类土地单位面积租金y(万元)与该
地段离开市中心的距离x(km)关系如图所示,
其中l1表示商业用地,l2表示工业用地,l3表
示居住用地,该市规划局单位面积租金最高为
标准规划用地,应将工业用地划在( )
A.与市中心距离分别为3km和5km的圆环区域内
B.与市中心距离分别为1km和4km的圆环形区域内
C.与市中心距离为5km的区域外 D.与市中心距离为5km的区域内
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中的横线上.
13.已知直线![]() 过点
过点![]() ,且与
,且与![]() 轴、
轴、![]() 轴的正半轴分别交于
轴的正半轴分别交于![]() 两点,
两点,![]() 为坐标原
为坐标原
点,则三角形![]() 面积的最小值为 .
面积的最小值为 .
14.以正方体ABCD—A1B1C1D1的8个顶点中4个为顶点,且4个面均为直角三角形的四面体是 (只要写出一个四面体即可).
15.若双曲线![]() 的焦点到相应于该焦点的准线的距离是2,则k= .
的焦点到相应于该焦点的准线的距离是2,则k= .
16.若含有集合A={1,2,4,8,16}中三个元素的A的所有子集依次记为B1,B2,B3,…,Bn(其中n∈N*),又将集合Bi(i=1,2,3,…,n)的元素的和记为![]() ,则
,则![]()
![]() =
.
=
.
高三数学期末综合练习(七)
班级 姓名 学号 得分
一. 选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二. 填空题(每小题4分,共16分)
13. ; 14. ;
15. ; 16. ;
三、解答题:(本大题6个小题,共74分)各题解答必需答在答题卡Ⅱ上(必需写出必要
的文字说明、推理过程或计算步骤)。
17.(本小题满分12分) 已知数列![]() 满足
满足![]()
(Ⅰ)求证:数列![]() 为等差数列;
为等差数列;
(Ⅱ)试问![]() 是否是数列
是否是数列![]() 中的项?如果是,是第几项;如果不是,请说明理由.
中的项?如果是,是第几项;如果不是,请说明理由.
18.(本小题满分12分)在任何两边都不相等的锐角三角形ABC中,已知角A、B、C的对边分别为a、b、c,且![]() (Ⅰ)求角B的取值范围;
(Ⅰ)求角B的取值范围;
(Ⅱ)求函数![]() 的值域;(Ⅲ)求证:
的值域;(Ⅲ)求证:![]()
19.(本小题满分12分)
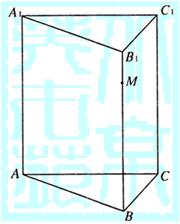
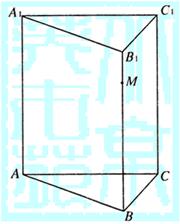
如图,已知正三棱柱ABC—A1B1C1的底面边长为1,点M在侧棱BB1上.
(Ⅰ)若BM=![]() ,求异面直线AM与BC所成的角;
,求异面直线AM与BC所成的角;
(Ⅱ)当棱柱的高BB1等于多少时,AB1⊥BC1?请写出你的证明过程.
|
20.(本小题满分12分)学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为![]() ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以![]() 轴为对称轴、
轴为对称轴、![]() 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为![]() . 观测点
. 观测点![]() 同时跟踪航天器.
同时跟踪航天器.
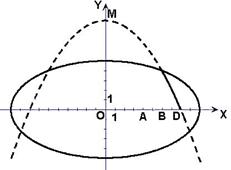 (1)求航天器变轨后的运行轨迹所在的曲线方程;
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在![]() 轴上方时,观测点
轴上方时,观测点![]() 测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
21.(本小题满分14分)直角坐标平面内,△ABC的两上顶点A、B的坐标分别为A(-1,0)、B(1,0),平面内两点G、M同时满足以下条件:①![]() ;②
;②![]() ;③
;③![]()
(Ⅰ)求△ABC的顶点C的轨迹方程;
(Ⅱ)过点P(2,0)的直线l与△ABC的顶点C的轨迹交于E、F两点,求![]() 的取值范围.
的取值范围.
22.(本小题满分12分)数列![]() 的前n项和为Sn,满足:
的前n项和为Sn,满足:![]() ,
,![]()
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)设数列![]() 的公比为
的公比为![]() ,数列
,数列![]() 满足
满足![]() 的
的
通项公式;
(3)记![]()
高三数学期末综合练习(七)
参考答案及评分标准
一、选择题:本大题共12小题,每小题5分,共60分.
1.A 2.B 3.C 4.C 5. C 6.A 7.A 8.D 9.D 10.B 11.C 12.B
二、填空题:本大题共4小题,每小题4分,共16分.
13.4 14.四面体A1ABC(不唯一) 15.6 16.186
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.解:(Ⅰ)当![]() …………2分
…………2分
两边同除以![]() ,…………4分
,…………4分
即![]() 成立,
成立,
∴![]() 为首项,d=4为公差的等差数列. …………6分
为首项,d=4为公差的等差数列. …………6分
(Ⅱ)由(Ⅰ)得,![]() ……8分
……8分
∴![]() …………9分
…………9分
设![]() 是数列
是数列![]() 的第t项,则
的第t项,则![]()
解得,t=11∈N*,………11分
∴![]() 是数列
是数列![]() 的第11项.…………12分
的第11项.…………12分
18.解:(Ⅰ)∵![]() ∴
∴![]()
∴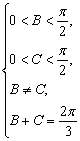 ∴
∴![]() …………4分
…………4分
(Ⅱ)∵![]() …………5分
…………5分
由(Ⅰ)得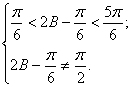 …………6分
…………6分
∴![]() ,∴函数
,∴函数![]() 的值域为(
的值域为(![]() ).……8分
).……8分
(Ⅲ)∵![]() ∴
∴![]() …………9分
…………9分
![]() ,∵
,∵![]()
∴![]() …………11分 ∴
…………11分 ∴![]() …………12分
…………12分
19.解:(Ⅰ)在正三棱柱ABC—A1B1C1中,B1B⊥底面ABC,
|
∴![]()
![]() ,……4分
,……4分
又∵![]()
∴![]() …………5分
…………5分
异面直线AM与BC所成的角为![]() ……6分
……6分
(Ⅱ)∵![]() ……8分
……8分
令![]() ,
,
即![]() …………11分
…………11分
∴当![]() 时,AB1⊥BC1.…………12分
时,AB1⊥BC1.…………12分
20.解:(1)设曲线方程为![]() , 由题意可知,
, 由题意可知,![]() .
. ![]() .
……3
.
……3
![]() 曲线方程为
曲线方程为![]() .
……6分
.
……6分
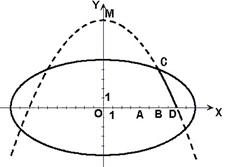 (2)设变轨点为
(2)设变轨点为![]() ,根据题意可知
,根据题意可知
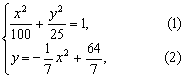 得
得 ![]() ,
,
![]() 或
或![]() (不合题意,舍去).
(不合题意,舍去).
![]() .
……8
.
……8
得 ![]() 或
或![]() (不合题意,舍去).
(不合题意,舍去). ![]()
![]() 点的坐标为
点的坐标为![]() ,
……10
,
……10
![]() .
.
答:当观测点![]() 测得
测得![]() 距离分别为
距离分别为![]() 时,应向航天器发出变轨指令.
……12
时,应向航天器发出变轨指令.
……12
21.解:(Ⅰ)设点C,G的坐标分别为![]() ,
,
![]()
![]() 0
0
![]() , …………2分
, …………2分
由![]() ,知点M的坐标为(0,y0), ……3分
,知点M的坐标为(0,y0), ……3分
由![]() ,可得
,可得![]()
∴![]()
点C的轨迹方程是![]() …………6分
…………6分
(Ⅱ)直线l的斜率为k(k≠0),则它的方程为y=k(x-2),
由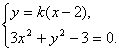 可得
可得![]() …………8分
…………8分
其中![]()
∴![]() …………9分
…………9分
设两交点E、F的坐标分别为 ![]() ,
,
由韦达定理得:![]()
又因为![]() 从而
从而
![]()
![]() …10
…10
又![]()
∴![]() 的取值范围是(3,
的取值范围是(3,![]() ). …………12
). …………12
22.解:(1)![]() ①,
①, ![]() ②
②
②-①得:![]() ,∴
,∴![]()
又![]() 解得:
解得:![]()
∴![]() , ∴
, ∴![]() 是等比数列.
------------------5分
是等比数列.
------------------5分
(2)![]() ∴
∴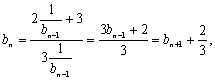
∴![]() ∴数列
∴数列![]() 为等差数列,
为等差数列,![]() -----9分
-----9分
(3)![]()
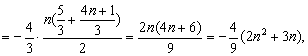
当![]() 为减函数, ∴
为减函数, ∴![]() ----------------14分
----------------14分