高三数学期末综合练习（五）

一、选择题：（本大题12个小题，每小题5分，共60分）各题答案必需答在答题卡上。

1. 如果是第一象限角, 那么恒有　　　　　　　　　　　　　　　　　　　 (　 )

A. 　　　　B. 　　 C. 　　　 D.

2. 设a、b、cR, 则是不等式恒成立的　　　　(　 )

A. 充分不必要条件　　　　　　　　　　　　 B.　必要不充分条件

C. 既不充分也不必要条件　　　　　　　　　 D.　充要条件

3. 一个等差数列(公差不为零), 令，，

, 则下列关系式中正确的是　　　　　　　　　　  (　 )

A. 　　 B. 　　 C.  　　 D.

4. 把函数的图象向左平移m个单位, 所得图象关于y轴对称, 则m的最小值为　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 )

A. 　　　　　　　B. 　　　　　　　C. 　　　　　　　 D.

5. 设※是集合A中元素的一种运算, 如果对于任意的x、y, 都有x※y, 则称运算※对集合A是封闭的, 若M则对集合M不封闭的运算是

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  (　 )

A. 加法　　　　　　 B.  减法　　　　　  C.　乘法　　　　　　 D.  除法

6. 若函数的图象可由函数的图象绕原点顺时针旋转90°得到, 则等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 )

A. 　　　　 B. 　　　　　 C. 　　　　 D.

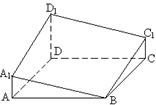7. 图中多面体是经过正四棱柱底面顶点B作截面A₁BC₁D₁而截得

的, 且AA₁CC₁. 已知截得面A₁BC₁D₁与底面ABCD成45°

的二面角, AB1, 则这个多面体的体积为　　　　　　  ( 　)

 A. 　　　　 B. 　　　　 C. 　　　　D.

8. 设F₁、F₂是双曲线的两个焦点, 点P在双曲线上, 且·

·, 则a的值等于　　　　　　　　　　　　  (　 )

A.  2　　　　　　 B.　1　　　C. 　　　　 D.

9. 设，则下列不等式成立的是　　　　　　　 (　 )

　A 　　　　 B 　 C 　D

10. 已知向量,, 则与夹角的范围为　　　　　　　　　　　　　　　　　　　　　　　　　  (　 )

A.　　　　 B.　　　　C.  　　　D.  

11. 已知向量，实数m，n满足

　 的最大值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．2　　　　　　　　　　　　B．3　　　　　　　　　　　　C．4　　　　　　　　　　　　D．16

12. 已知的图象经过点, 且, 记(其中是两个不相等的正实数), 则p与q的大小关系是　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 )

A. 　　　　　 B. 　　　　　 C. 　　　　　 D.

二. 填空题：(本大题共4小题；每小题4分，共16分)

13. 若把圆x²+y²+2x－4y=0按向量a=（1，2）平移后，恰好与直线x－2y+λ=0相切，则实数λ的值为　　　　  .

14. 若实数x, y满足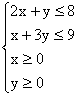, 则的最大值为　　　　　　 .

15. 已知奇函数满足条件, 且当时,,则的值是　　　　　　　　.

16. 有以下四个命题①的最小值是；②已知, 则；③在R上是增函数；

④函数的图象的一个对称点是；

其中真命题的序号是　　　　　　　　　   (把你认为正确命题的序号都填上)

高三数学期末综合练习（五）

班级　　　　 姓名　　　　 学号　　　 得分

一. 选择题（每小题5分，共60分）　　　　　　　　　　　　　　　　　　　 　　　　　　

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二. 填空题（每小题4分，共16分）

13. 　　　　　　　; 　　　　　　　 14. 　　　　　　　　; 　

　 15.　　　　　　　　 ;　　　　　　　 16.　　　　　　　 ;　　　

　

三、解答题：（本大题6个小题，共74分）各题解答必需答在答题卡Ⅱ上（必需写出必要

的文字说明、推理过程或计算步骤）。

17.（本题12分）已知函数f（x）=log₂（x+m），且f（0）、f（2）、f（6）成等差数列．

（1）求实数m的值；

（2）若a、b、c是两两不相等的正数，且a、b、c成等比数列，试判断f（a）+f（c）与2f（b）的大小关系，并证明你的结论．

18. (本题12分) 已知向量, 向量b与向量a的夹角为, 且a·b,

(1) 求向量b;

(2) 向量, 其中A、C是△ABC的内角, 若三角形的三内角A、B、C依次成等差数列, 且与x轴垂直. 试求的取值范围.

19. (本题12分) 如图, 四棱锥P－ABCD的底面是正方形, PA⊥底面ABCD, PA＝AD＝2, 点M、N 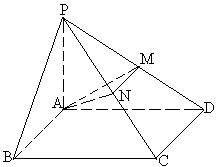分别为棱PD、PC的中点.

(1) 求证: PD⊥平面AMN;

(2) 求二面角P－AN－M的大小.

20.（本题12分）已知为抛物线上任意一点, 直线l为过点A的切线, 设直

线l交y轴于点B. Pl, 且.

(1) 当A点运动时, 求点P的轨迹方程;

(2) 求点到动直线l的最短距离, 并求此时l的方程.

21. (本题12分)

函数

　 （I）若

　 （Ⅱ）若

22. （本题14分）已知函数.

(1) 求的反函数及其定义域;

(2) 数列, , 设, 数列的前n项和为, 试比较与的大小, 并证明你的结论.

高三数学期末综合练习（五）

参考答案及评分标准

一. 选择题（每小题5分，共60分）　　　　　　　　　　　　　　　　　　　　　　 

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	B	C	C	B	D	D	D	B	C	D	D	B

二. 填空题（每小题4分，共16分）

13. 3或13; 　　　14. 　　 7　　　;　　　 15. 　　　－1　　　; 　　　16. 　 ③ ④　;

三. 解答题（共74分）

17．（本小题满分12分）

解: （1）由f（0）、f（2）、f（6）成等差数列，

可得2log₂（2+m）=log₂m+log₂（6+m），

即（m+2）²=m（m+6）且m>0，解得m=2． 6分

（2）由f（x）=log₂（x+2），可得2f（b）=2log₂（b+2）=log₂（b+2）²，

f（a）+f（c）=log₂（a+2）+log₂（c+2）=log₂［（a+2）（c+2）］，　 8分

∵a、b、c成等比数列，∴b²=ac，　9分

又a、b、c是两两不相等的正数，

故（a+2）（c+2）=ac+2（a+c）+4>ac+4+4=b²+4b+4=（b+2）²， 10分

∴log₂［（a+2）（c+2）］>log₂（b+2）²，即f（a）+f（c）>2f（b）　12分

18．（本小题满分12分）

解: 设, 则,……(1分)且.……(3分)

∴解得或或……(5分)

(2), ……(6分) ∵b⊥x轴, ∴,……(7分)

∴b＋c＝,……(8分)

∴ b＋c ²＝

……(10分)

∵, ∴.……(12分)

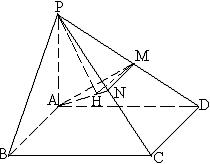19．（本小题满分12分）

证明: (1) ∵ABCD是正方形, ∴CD⊥AD

∵PA⊥底面ABCD,

∴AD是PD在平面ABCD内的射影,∴CD⊥PD……(2分)

在△PCD中M、N分别是PD、PC的中点, 则MN∥CD,

∴PD⊥MN, 在△PCD中PA＝AD＝2, M为PD的中点.

∴PD⊥AM, ∴PD⊥平面AMN……(4分)

(2)　∵作MH⊥AN于H, 连接PH, ∵PM⊥平面AMN, ∴PH⊥AN , ∠PHM为二面角P—AN—M的平面角. (10分)

∵PM⊥平面AMN, ∴PM⊥MH. 在Rt△AMN中, MH

在Rt△PMH中, tan∠PHM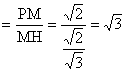,……(11分)

∴∠PHM＝60°, 则二面角P—AN—M的大小为60°……(12分)

20．（本小题满分12分）

解: (1)设, 因为,……(1分)

所以过点A的切线方程为……(2分)

令, 则, B点坐标为.……(3分)

又, ∴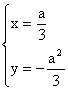消去a, 得……(6分)

(2)设C到l的距离为d, 则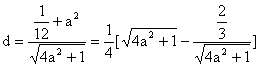……(8分)

设, 则为t的增函数……(10分)

∴……(11分)

故C到l的最短距离为, 此时l的方程为……(12分)

21．（本小题满分12分）

解: （I）解f(x)=10－f(2m－x)若m=－1，则f(x)关于（－1，5）对称.　 （1分）

  　　　所以a=1，　　　　  （3分）

　　　　即　　　 （4分）

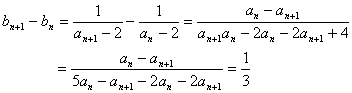
所以{b_n}是以为公差的等差数列.　　　　　  （6分）

　　 （7分）

所以　　　　（8分）

　 （II）证明：

　

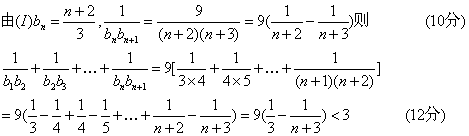
22．（本小题满分14分）

解: (1)设, 则,

∴……(1分)

,

∴或. ∴所求的反函数是:

其定义域是: .……(4分)

(2) ∵, ∴……(6分)

又,

∴……(8分)

……(9分)

∵,

则当时, 有,……(12分)

∴……(13分)

∴

……(14分)