高三数学期末综合练习(一)
一、选择题:(本大题12个小题,每小题5分,共60分)各题答案必需答在答题卡上。
1.若集合![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.数![]() 的大小关系是
的大小关系是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.条件![]() :不等式
:不等式![]() 的解;条件
的解;条件![]() :不等式
:不等式![]() 的解,则
的解,则![]() 是
是![]() 的
的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.非充分非必要条件
4.若![]() 的图象是两条平行直线,则
的图象是两条平行直线,则![]() 的值是
的值是
A.![]() 或
或![]() B.
B.![]() C.
C.![]() D.
D.![]() 的值不存在
的值不存在
5.在![]() 内使
内使![]() 成立的
成立的![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.若函数![]() 的图象过点
的图象过点![]() ,则函数
,则函数![]() 的图象必过点
的图象必过点
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.在正项等比数列![]() 中,
中,![]() 是方程
是方程![]() 的两个根,则
的两个根,则![]() 的值为
的值为
A.32 B.64 C.![]() D.256
D.256
8.若函数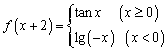 ,则
,则![]()
A.![]() B.
B.![]() C.2
D.
C.2
D.![]()
9.已知直线![]() ,其中
,其中![]() 为实数,当这两条直线的夹角在
为实数,当这两条直线的夹角在![]() 内变动时,
内变动时,![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知![]() 是
是![]() 上的增函数,点
上的增函数,点![]() 在它的图象上,
在它的图象上,![]() 是它的反函数,那么不等式
是它的反函数,那么不等式![]() 的解集为
的解集为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 和
和![]() ,若
,若![]() 是
是![]() 的等比中项,
的等比中项,![]() 是
是![]() 与
与![]() 的等差中项,则椭圆的离心率是
的等差中项,则椭圆的离心率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.某金店用一杆不准确的天平(两边臂不等长)称黄金,某顾客要购买![]() 黄金,售货员先将
黄金,售货员先将![]() 的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将
的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将![]() 的砝码放入右盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金
的砝码放入右盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金
A.大于![]() B.小于
B.小于![]() C.大于等于
C.大于等于![]() D.小于等于
D.小于等于![]()
二、填空题:(本大题4个小题,每小题4分,共16分)各题答案必须填写在答题卡Ⅱ上(只填结果,不要过程)。
13.已知平面向量![]() ,
,![]() ,若
,若![]() ,则实数
,则实数![]() =_______.
=_______.
14.已知![]() 满足约束条件
满足约束条件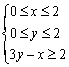 ,则
,则![]() 的最大值是______________.
的最大值是______________.
15.已知![]() 点是圆
点是圆![]() 上任一点,
上任一点,![]() 点关于直线
点关于直线![]() 的对称点也在圆上,那么实数
的对称点也在圆上,那么实数![]() 等于____________.
等于____________.
16.已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() 等于_____________.
等于_____________.
 高三数学期末综合练习(一)
高三数学期末综合练习(一)
一. 选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二. 填空题(每小题4分,共16分)
13. ; 14. ;
15. ; 16. ;
三、解答题:(本大题6个小题,共74分)各题解答必需答在答题卡Ⅱ上(必需写出必要的文字说明、推理过程或计算步骤)。
17.(12分)在![]() 中,
中,![]() 是角
是角![]() 所对的边,
所对的边,![]() 是该三角形的面积,且
是该三角形的面积,且![]() 。(Ⅰ)求角
。(Ⅰ)求角![]() 的度数;
的度数;
(Ⅱ)若![]() ,求
,求![]() 的值。
的值。
18.(12分)已知实数![]() 满足不等式
满足不等式![]() ,解关于
,解关于![]() 的不等式:
的不等式:![]()
19.(12分)已知函数![]() 。
。
(Ⅰ)若关于![]() 的方程
的方程![]() 的解都在区间
的解都在区间![]() 内,求实数
内,求实数![]() 的范围;
的范围;
(Ⅱ)若函数![]() 在区间
在区间![]() 上单调递增,求正实数
上单调递增,求正实数![]() 的取值范围。
的取值范围。
20.(12分)某商场只设有超市部、服装部、家电部三个部门,共有200名售货员,计划三个部门日营业额共为55万元,各部门的商品每1万元营业额所需售货员人数如表(1),每1万元营业额所得利润如表(2),若商场预期每日的总利润为![]() 万元,且满足
万元,且满足![]() ,又已知商场分配给三个部门的日营业额为正整数万元,问商场怎样分配营业额给三个部门?各部门分别安排多少名售货员?
,又已知商场分配给三个部门的日营业额为正整数万元,问商场怎样分配营业额给三个部门?各部门分别安排多少名售货员?
表(1) 表(2)
| 部门 | 每1万元营业额所需人数 |
| 超市部 | 4 |
| 服装部 | 5 |
| 家电部 | 2 |
| 部门 | 每1万元营业额所需人数 |
| 超市部 | 0.3万元 |
| 服装部 | 0.5万元 |
| 家电部 | 0.2万元 |
21.(12分)设抛物线过定点![]() ,且以直线
,且以直线![]() 为准线
为准线
(Ⅰ)求抛物线顶点的轨迹![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,轨迹
,轨迹![]() 上是否存在满足
上是否存在满足![]() 的
的![]() 两点?证明你的结论。
两点?证明你的结论。
22.(14分)设![]() 有唯一解,
有唯一解,![]() 。
。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若![]() 且
且![]() ,求证:
,求证:![]()
(Ⅲ)是否存在最小整数![]() ,使得对于任意
,使得对于任意![]() ,有
,有![]() 成立,若存在,求出
成立,若存在,求出![]() 的值;若不存在,说明理由。
的值;若不存在,说明理由。
高三数学期末综合练习(一)
参考答案及评分标准
一、选择题:(本大题12个小题,每小题5分,共60分)
CDAB,DABC,CBDA
二、填空题:(本大题4个小题,每小题4分,共16分)
13.0; 14.3; 15.3; 16.10
三、解答题:(本大题6个小题,共74分)
17.(12分)
解:(Ⅰ)由已知等式得:![]() …………(2分)
…………(2分)
![]() ………………(5分)
………………(5分)
![]() ………………………………………………………………(6分)
………………………………………………………………(6分)
(Ⅱ)![]() ……………………………………(8分)
……………………………………(8分)
![]() ……………………(11分)
……………………(11分)
![]() ………………………………………………………………(12分)
………………………………………………………………(12分)
18.(12分)
解:由![]()
![]() ………………………………(2分)
………………………………(2分)
①当![]() 时,
时,![]() ;……………………………(6分)
;……………………………(6分)
②当![]() 时,
时,![]() ;…………………………………………(8分)
;…………………………………………(8分)
③当![]() 时,
时,![]() 。………………………………(11分)
。………………………………(11分)
综上,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 。………………………(12分)
。………………………(12分)
19.(12分)
解:(Ⅰ)![]()
 ………………………………(7分)
………………………………(7分)
(Ⅱ)![]()
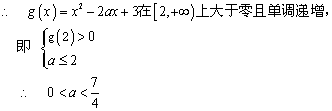 ………………………(12分)
………………………(12分)
20.(12分)
解:设商场分配给超市部、服装部、家电部的营业额依次为![]() 万元,
万元,![]() 万元,
万元,![]() 万元(
万元(![]() 均为正整数),由题意得:
均为正整数),由题意得:
 ………………………………(5分)
………………………………(5分)
由(1),(2)得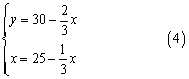 ………………………………(7分)
………………………………(7分)
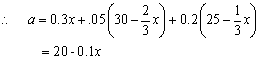 ………………………………(8分)
………………………………(8分)
![]()
![]() ………………………………(9分)
………………………………(9分)
 ………………(11分)
………………(11分)
答:分配给超市部、服装部、家电部的营业额分别为12万元,22万元,21万元,售货员人数分别为48人,110人,42人;或者分配给三部门的营业额依次为15万元,20万元,20万元,售货员人数分别为60人,100人,40人。……………………(12分)
21.(12分)
解:(Ⅰ)设抛物线顶点为![]() ,则抛物线的焦点为
,则抛物线的焦点为![]() ,由抛物线的定义可得:
,由抛物线的定义可得:
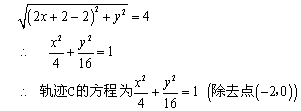 ……………………………(6分)
……………………………(6分)
(Ⅱ)不存在。…………………………………………………………(7分)
设过点![]() ,斜率为
,斜率为![]() 的直线方程为
的直线方程为![]() (斜率不存在时,显然不合题意),………………………………………………………………………………(8分)
(斜率不存在时,显然不合题意),………………………………………………………………………………(8分)
由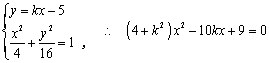 …………………………(9分)
…………………………(9分)
由![]() ………………………………………………………(10分)
………………………………………………………(10分)
假设在轨迹![]() 上存在两点
上存在两点![]() ,令
,令![]() 的斜率分别为
的斜率分别为![]() ,则
,则![]()
显然不可能满足![]()
∴轨迹![]() 上不存在满足
上不存在满足![]() 的两点。………………………………(12分)
的两点。………………………………(12分)
22.(14分)(Ⅰ)解:由![]() ,可以化为:
,可以化为:![]()
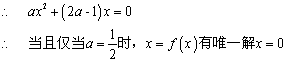 ………………………………(1分)
………………………………(1分)
从而![]() …………………………………………………………(3分)
…………………………………………………………(3分)
又由已知![]() ,得:
,得:![]()
![]() , 即
, 即 ![]()
∴数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,…………………………(4分)
的等差数列,…………………………(4分)
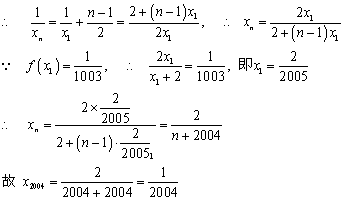 ……………………(8分)
……………………(8分)
(Ⅱ)证明:![]() ……(9分)
……(9分)
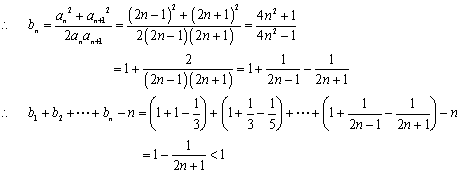 (12分)
(12分)
(Ⅲ)解:由于![]() ,若
,若![]() 恒成立
恒成立
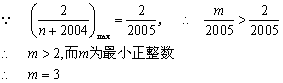 ………………………………(14分)
………………………………(14分)