2006年甘肃省兰州一中高三第一学期12月月考试卷
数 学 (文)
第Ⅰ卷(选择题,共60分)
一、选择题:本题共12小题,每小题5分,共60分;每小题给出的四个选项中,只有一项是符合要求的.将每题正确选项的序号填在答题卡的相应位置.
1.若![]() ,则下列不等式 ①
,则下列不等式 ①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 中,正确的不等式有 ( )
中,正确的不等式有 ( )
A.1个 B.2个 C.3个 D.4个
2.不等式![]() >0的解集是 ( )
>0的解集是 ( )
A.{ x|-2<x<1或x>1 } B. { x|x<-2或x>1 }
C.{ x|x>-2 } D. 以上均不正确
3.函数y = x2 + b x + c(x∈[ 1,+∞))是单调函数的充要条件是 ( )
A.b<1 B.b≤-2 C.b>1 D.b≥-2
4.公差不为零的等差数列{an}中,a2,a3,a6成等比数列,则其公比q为 ( )
A.4 B.3 C.2 D.1
5.若 l1:x +(1+m) y = 2-m ;l2:2 m x + 4 y +16 = 0的图像是两条平行直线,则m的值是 ( )
A.m =1 B.m =1或m =-2 C.m =-2 D.m的值不存在
6.若直线2x-y+c = 0按向量 ![]() =(1,-1)平移后与圆
=(1,-1)平移后与圆 ![]() 相切,则c的值为 ( )
相切,则c的值为 ( )
A.2或-8 B. 6或-4 C. 4或-6 D.8或-2
7.设若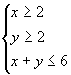 ,则目标函数 z = x + 3 y 的最大值是 ( )
,则目标函数 z = x + 3 y 的最大值是 ( )
A. 8 B.10 C. 12 D.14
8.双曲线以椭圆![]() 长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为 ( )
长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为 ( )
A.±2 B.![]() C.
C.![]() D.
D.![]()
9.若0<a<1,0<x≤y<1,且loga x·logay = 1,则 x y ( )
A.无最大值也无最小值 B.无最大值而有最小值
C.有最大值而无最小值 D.有最大值也有最小值
10.已知sinα+ cosα= tanα ( 0<α<![]() ) ,则α∈( )
) ,则α∈( )
A.(0,![]() ) B.(
) B.(![]() ,
,![]() ) C.(
) C.(![]() ,
,![]() ) D.(
) D.(![]() ,
,![]() )
)
11.已知函数 y = f ( x ) 与 y = g ( x )的图像如图所示,则函数F ( x ) =
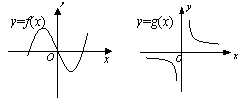 f ( x ) · g ( x
) 的图像只可能是 ( )
f ( x ) · g ( x
) 的图像只可能是 ( )
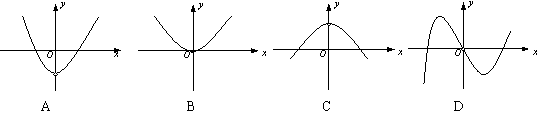
12.设数集M ={ x|m![]() x
x ![]() m +
m +![]() },N ={ x|n-
},N ={ x|n-![]()
![]() x
x ![]() n },且M、N都是集合{ x|0
n },且M、N都是集合{ x|0![]() x
x ![]() 1 }的子集,如果把b-a叫做集合{ x|a
1 }的子集,如果把b-a叫做集合{ x|a![]() x
x ![]() b }的“长度”,那么集合M∩N的“长度”的最小值是( )
b }的“长度”,那么集合M∩N的“长度”的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
答 题 卡
一、选择题:本大题共12小题,每小题5分,共60分.
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 |
|
|
|
|
|
|
|
|
|
|
|
|
第Ⅱ卷(非选择题,共90分)
二、填空题:本题共4小题,每小题4分,共16分;答案填在题中的横线上.
13.已知函数![]() (x)= a sin2x
+ b tanx,且
(x)= a sin2x
+ b tanx,且![]() (-2)= 4,那么
(-2)= 4,那么![]() (π+ 2)= .
(π+ 2)= .
14. 已知![]() ,则不等式x+(x +2)·f (x)
,则不等式x+(x +2)·f (x)![]() 5的解集是 .
5的解集是 .
15.双曲线![]() 的两个焦点为F1,F2,点P在双曲线上,若
的两个焦点为F1,F2,点P在双曲线上,若![]() ,则P到x轴的距离为
.
,则P到x轴的距离为
.
16.已知A (![]() ,0 ),B是圆
,0 ),B是圆![]() 为圆心)上一动点,线段AB的垂直平分线交BF于P,则动点P的轨迹方程为
.
为圆心)上一动点,线段AB的垂直平分线交BF于P,则动点P的轨迹方程为
.
三、解答题: 6小题,共74分;写出必要的文字说明、证明过程或演算步骤.
17.(12分)已知函数
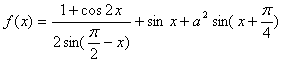
(1)求函数y = f(x)的单调递增区间;
(2)若函数 y = f(x)的最小值为 ![]() ,试确定常数a的值.
,试确定常数a的值.
18.(12分)设a > 0,解关于x的不等式 1-![]() < a .
< a .
19.(12分) 已知函数![]() ,定义数列{a n},使a1 = 4 ,a2 = f(a1),…,a n+1
= f(a n)
.
,定义数列{a n},使a1 = 4 ,a2 = f(a1),…,a n+1
= f(a n)
.
(1)求证:数列{![]() }是等差数列;
}是等差数列;
(2)设数列 { a n·a n+1} 的前n项和为S n,求证:S n<8.
20.(12分) 对于函数 f(x),若存在 x0∈R 使f(x0)= x0 成立,则称x0为
f(x)的不动点.已知函数![]() 有且仅有两个不动点0,2.
有且仅有两个不动点0,2.
(1)求函数f(x)的解析式;
(2)当x ∈ ( 1,2 ]时,不等式 2 f(x +1)> m 有解,求实数m的取值范围.
21.(12分)已知定点A(1,0),动点M满足 ![]() ,其中O是坐标原点,k是参数.
,其中O是坐标原点,k是参数.
(1) 当k > 0且k ≠ 1时,求动点M的轨迹方程,并说明它表示什么曲线;
(2) 当k < -1时,求该曲线离心率的范围.
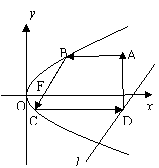
| |
(1)设B、C两点的坐标分别为(x1,y1),(x2,y2) ,证明:y1 y2 = - p2;
(2)求抛物线的方程;
(3)已知该抛物线上的动弦MN的中点P的轨迹方程为y 2 = 2(x + 1)( 其中x > 1) ,求证:弦MN所在直线经过定点,并求出该定点的坐标.
2006年甘肃省兰州一中高三第一学期12月月考试卷
数学参考答案及评分标准(文)
一、选择题:本大题共12小题,每小题5分,共60分.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | D | B | A | D | D | C | C | C | A | B |
二、填空题:本大题共4小题,每小题4分,共16分.
13.-4; 14.![]() ; 15.
; 15.![]() ; 16.
; 16.![]() .
.
三、解答题:6小题,共74分;应写出必要的文字说明、证明过程或演算步骤 .
17.(12分)解:
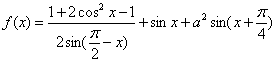
![]() …3分
…3分
![]() …………………6分
…………………6分
(1)由x + ![]() ∈[
∈[![]() -
-![]() ,
,![]() +
+![]() ](k∈Z)得
](k∈Z)得
x∈[![]() -
-![]() ,
,![]() +
+![]() ](k∈Z)
](k∈Z)
∵![]() ∴
∴![]()
∴ 函数y = f(x)的单调递增区间是
[![]() -
-![]() ,
,![]() -
-![]() )∪ (
)∪ ( ![]() -
-![]() ,
,![]() +
+![]() ](k∈Z).…9分
](k∈Z).…9分
(2)由已知得![]() , ∴ a = ±2 .………………………12分
, ∴ a = ±2 .………………………12分
18.(12分)解:原不等式可化为-a < 1-![]() < a ……………………………2分
< a ……………………………2分
即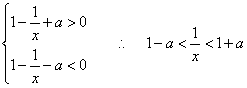 ……………………………4分
……………………………4分
∵ a >0 ∴1+ a >0 ……………………………5分
①当1-a > 0即0< a <1时, ![]() < x <
< x <
![]() ; …………………………7分
; …………………………7分
②当1-a = 0即a =1时,原不等式可化为2x-1 > 0, ∴x > ![]() ;…………9分
;…………9分
③当1-a < 0即a >1时,等价于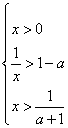 或
或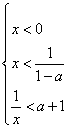
∴ x > ![]() 或 x <
或 x <
![]() ………………………………………………11分
………………………………………………11分
综上,当a >1时,原不等式的解集为{x
x > ![]() 或x <
或x < ![]() };
};
当a =1时,原不等式的解集为{x x >![]() };
};
当0< a <1时,原不等式的解集为{ x ![]() < x <
< x <
![]() }.……………12分
}.……………12分
19.(12分)解:(1)∵a n+1 = f(a n) ∴![]()
∴![]()
又![]() ∴数列{
∴数列{![]() }是以
}是以![]() 为首项,以
为首项,以![]() 为公差的等差数列.…………5分
为公差的等差数列.…………5分
(2)由(1)可知![]() …………7分
…………7分
∴![]() …………………………9分
…………………………9分
∴S n = a1 a 2 + a2 a 3 + … + a n a n+1
![]()
![]() …………………………………………12分
…………………………………………12分
20.(12分)解:(1)由已知得:
![]() ………………6分
………………6分
(2) ∵ ![]()
当x∈ (1,2]时,函数![]() 单调递增.
单调递增.
∴![]() …10分 ∴
…10分 ∴ ![]() . ……12分
. ……12分
21.(12分)解:(1)设M(x,y), ∵![]()
∴ 由题可得:(-k ) x 2 + x 2 + y 2 = 1-k ,
即 (1-k)x 2 + y 2 = 1-k 为所求的轨迹方程.
∵k > 0且k ≠ 1, ∴ 方程可化为![]()
当k > 1时,动点M的轨迹是一条双曲线;
当0< k <1时,动点M的轨迹是一个椭圆. ……………………6分
(2)当k < -1时,动点M的轨迹是椭圆,方程为![]()
其中a 2 = 1-k , b 2 = 1 ,c 2 = a 2 - b 2 = - k, …………………8分
∴
![]()
∵
k <-1 ∴ ![]() ∴
∴![]() .…………………12分
.…………………12分
22.(14分)解:(1)由题可知,光线BC必过抛物线的焦点F(![]() ,0)
,0)
设直线BC的方程为x = my
+ ![]() ,将其代入抛物线方程y2 =2px得y 2 -2p my -p 2 = 0
,将其代入抛物线方程y2 =2px得y 2 -2p my -p 2 = 0
∴ y1 y2 = - p2. ………………………………………… 4分
(2)由题可知,点A(6,4)关于直线 l:x - y – 7 = 0的对称点E(11,-1)在直线CD上,∴ y2 = -1 ,又y1 = 4 ∴ 由y1 y2 = -p2得p=2 ,则抛物线的方程为y2 = 4x. ………………………………………… 8分
(3)设M(x1,y1)、N (x2,y2)、P(a,b) ∴2a = x1 + x2 ,2b = y1 + y2
由题可知,直线MN的斜率存在且不为零,∴设直线MN的斜率为k,
则由 两式相减得(y1-y2) (y1 + y2) =
4 (x1-x2)
两式相减得(y1-y2) (y1 + y2) =
4 (x1-x2)
∴ k = ![]() 则
则 ![]()
又已知点P的轨迹方程为y2 =2(x + 1) (x > 1) , ∴ b2 =2(a + 1)
将 ![]() 代入得
代入得 ![]() ,
,
则经过点P且斜率为k的直线MN的方程为y = k(x-![]() )+
)+ ![]()
即 y = k x + k = k (x + 1)
∴ 弦MN所在直线经过定点,该定点的坐标为(-1,0). ……………… 14分