高明一中高三级第一学期第一次考试
数学试卷
一.选择题(每题5分,共10题,满分50分)
1 ![]() 设集合P={1,2,3,4},Q={
设集合P={1,2,3,4},Q={![]() },则P∩Q等于
},则P∩Q等于
A.{1,2}
B ![]() {3,4}
C
{3,4}
C ![]() {1} D
{1} D ![]() {-2,-1,0,1,2}
{-2,-1,0,1,2}
2 ![]() 设函数f ( x )=2x+3,g (x+2)=f ( x ),则g ( x )的表达式是
设函数f ( x )=2x+3,g (x+2)=f ( x ),则g ( x )的表达式是
A.2x+1 B ![]() 2x-1 C
2x-1 C
![]() 2x-3 D
2x-3 D
![]() 2x+7
2x+7
3 ![]() 函数
函数![]() 的定义域是:
的定义域是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4 ![]() 设0<a<1,实数x,y满足x+
设0<a<1,实数x,y满足x+![]() =0,则y关于x的函数的图象大致形状是 A
=0,则y关于x的函数的图象大致形状是 A

A
B
C
D
5 ![]() 函数
函数 ![]() 反函数是
反函数是
A ![]()
![]()
![]() B
B ![]()
![]() = -
= -![]()
![]()
C ![]()
![]() =
=![]()
![]() D
D ![]()
![]() =-
=-![]()
![]()
6 ![]() 命题“方程
命题“方程![]() 的解集是
的解集是![]() ”中,使用逻辑连结词的情况是
”中,使用逻辑连结词的情况是
A ![]() 没有使用逻辑连结词 B
没有使用逻辑连结词 B ![]() 使用了逻辑连结词“或”
使用了逻辑连结词“或”
C
![]() 使用了逻辑连结词“且” D
使用了逻辑连结词“且” D ![]() 使用了逻辑连结词“非”
使用了逻辑连结词“非”
7 ![]() 与函数y=x有相同图象的一个函数是
与函数y=x有相同图象的一个函数是
![]()
![]()
8 ![]() 函数
函数![]() 的反函数
的反函数
A ![]() 是奇函数,它在(0,+∞)上是减函数
是奇函数,它在(0,+∞)上是减函数 ![]() B
B ![]() 是偶函数,它在(0,+∞)上是减函数
是偶函数,它在(0,+∞)上是减函数 ![]()
C ![]() 是奇函数,它在(0,+∞)上是增函数
是奇函数,它在(0,+∞)上是增函数 ![]() D
D ![]() 是偶函数,它在(0,+∞)上是增函数
是偶函数,它在(0,+∞)上是增函数 ![]()
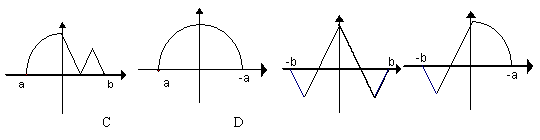
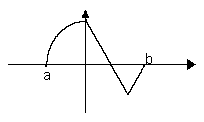 9
9 ![]() 已知y=
已知y=![]() (
(![]() )的图象如右图所示,则y=
)的图象如右图所示,则y=![]() 的图象为
的图象为
 | |||||
|
| ||||
10 ![]() 函数
函数![]() 的图象必不过
的图象必不过
A ![]() 第一象限 B
第一象限 B ![]() 第二象限 C
第二象限 C ![]() 第三象限 D
第三象限 D ![]() 第四象限
第四象限
二 ![]() 填空题(每题5分,共4题,满分20分)
填空题(每题5分,共4题,满分20分)
11 ![]() 奇函数
奇函数![]() 定义域是
定义域是![]() ,则
,则![]()
![]()
12 ![]() 函数
函数![]() 在区间[0,3]上的最大值是
在区间[0,3]上的最大值是 ![]() 最小值
最小值 ![]() 是
是 ![]()
13 ![]() 设函数f (x)的反函数是f -1(x)=
设函数f (x)的反函数是f -1(x)=![]() ,则f (4)=
,则f (4)=
![]()
14 ![]() 函数
函数![]() 的单调递减区间是
的单调递减区间是
![]()
三.解答题(共6题,满分80分)
15 ![]() (12分)已知函数f (x)=
(12分)已知函数f (x)=![]() (
(![]() ),求出它的反函数
),求出它的反函数
![]()
16 ![]() (12分)设函数
(12分)设函数![]() 的定义域为A,B=
的定义域为A,B=![]()
![]() ,且A
,且A![]() B=R,求实数
B=R,求实数![]() 的取值范围
的取值范围 ![]()
17.(14分)已知函数![]() 是偶函数,而且在
是偶函数,而且在![]() ,
,![]() 是减函数
是减函数 ![]()
⑴ 判断![]() 在
在![]() ,
,![]() 上是增函数还是减函数,并证明你的判断
上是增函数还是减函数,并证明你的判断 ![]()
⑵ 写出符合上述条件的一个函数 ![]()
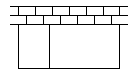
18 ![]() (14分)以墙为一边,用篱笆围成长方形的场地,并用平行于一边的篱笆隔开(如图)
(14分)以墙为一边,用篱笆围成长方形的场地,并用平行于一边的篱笆隔开(如图) ![]() 已知篱笆的总长为定值L,这块场地的长和宽各为多少时场地的面积最大?最大面积是多少?
已知篱笆的总长为定值L,这块场地的长和宽各为多少时场地的面积最大?最大面积是多少?
19 ![]() (14分)已知f (x)=log
a
(14分)已知f (x)=log
a![]() (a>0,a≠1).
(a>0,a≠1).
(Ⅰ)求f (x)的定义域;
(Ⅱ)判断f (x)的奇偶性并予以证明;
20 ![]() (14分)设
(14分)设![]() 为定义在
为定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() 的图象是经过点
的图象是经过点![]() ,斜率为1的射线,又在
,斜率为1的射线,又在![]() 的图象中有一部分是顶点在
的图象中有一部分是顶点在![]() ,且过点
,且过点![]() 的一段抛物线
的一段抛物线 ![]() 试求函数
试求函数![]() 的表达式,并作出其图象.
的表达式,并作出其图象.
参考答案
1 ![]() A 2
A 2 ![]() B 3
B 3 ![]() D 4
D 4 ![]() A 5
A 5 ![]() B
6
B
6 ![]() B 7
B 7 ![]() D 8
D 8 ![]() C 9
C 9 ![]() C 10
C 10 ![]() A
A
11 ![]() -1 ; 12
-1 ; 12 ![]() 最大值是2,最小值是-2; 13
最大值是2,最小值是-2; 13 ![]()
![]() ; 14
; 14 ![]() (2,+∞)
(2,+∞) ![]()
15 ![]() 由
由 ![]() =
=![]() 得
得![]()
![]() ——4分
——4分
∵![]()
∴ ![]() ——8分
——8分
∴函数f (x)=![]() (
(![]() )的反函数是
)的反函数是
f -1(x)=![]() ,
,![]() ——12分
——12分
16 ![]() 要使函数
要使函数![]() 有意义则
有意义则![]()
∴ ![]()
∴ A=![]()
![]()
![]() ——3分
——3分
B=![]()
![]()
=![]()
![]()
![]() ——3分
——3分
又因为A![]() B=R, 所以
B=R, 所以![]() 应满足
应满足 ![]() ——10分
——10分
即 ![]() ——12分
——12分
17 ![]() ⑴
⑴
![]()
![]() 在
在![]() ,
,![]() 上是增函数
——1分
上是增函数
——1分
证明:设![]()
∵ ![]() 是偶函数
是偶函数
∴ ![]() ,
,![]() ①
——3分
①
——3分
由假设可知,![]() ,
,![]() ,并且
,并且![]()
又已知![]() 在
在![]() ,
,![]() 是减函数
是减函数
∴ ![]() ②
——7分
②
——7分
将①代入②得 ![]() ——9分
——9分
由此可知,当![]() ,
,![]()
![]() ,且
,且![]() 时,有
时,有![]()
即函数![]() 在
在![]() ,
,![]() 上是增函数
上是增函数 ![]() ——11分
——11分
⑵ 符合上述条件的一个函数是 ![]()
![]() ——14分
——14分
18 ![]() 解法一:设长方形场地的宽为x,则长为L-3x
——1分
解法一:设长方形场地的宽为x,则长为L-3x
——1分
长方形场地的面积为
y=x(L-3x)=-3x2+Lx
![]() ———7分
———7分
其中![]() 即
即![]() ——8分
——8分
![]()
————————————10分
 ―――――13分
―――――13分
![]()
————————14分

19 ![]() (Ⅰ)由对数函数的定义知
(Ⅰ)由对数函数的定义知![]()
即![]() .
——2分
.
——2分
如果![]() ,则-1<x<1;
,则-1<x<1;
如果![]() ,则不等式组无解.
,则不等式组无解.
故f (x)的定义域为(-1,1) ——7分
(Ⅱ) f (x)的定义域为(-1,1)
∵ ![]() ,
,
∴ f (x)为奇函数. ——14分
20 ![]() 当
当![]() 时,设
时,设![]() ,
——1分
,
——1分
则由![]() ,即
,即![]() ,得
,得![]() ;
——3分
;
——3分
当![]() 时,设
时,设![]() ,
——4分
,
——4分
则由![]() ,
,
即![]() ,得
,得![]() ;
——6分
;
——6分
当![]() 时,
时,![]()
![]() —— 8分
—— 8分
故: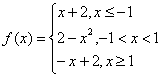 ——10分
——10分
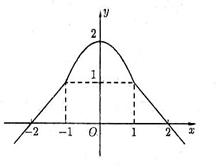 作图:4分
作图:4分