福建省永安九中2006届第一学期期中考试卷2005.11
高三数学(理科)
YCY (满分150分,考试时间120分钟)命题人:吴秉术
一 ![]() 选择题(本大题共12小题,每小题5分,共60分
选择题(本大题共12小题,每小题5分,共60分 ![]() 在每小题给出的中四选项中,只有一项是符合题目要求的
在每小题给出的中四选项中,只有一项是符合题目要求的 ![]() 请把正确选项的代号填在答题卡指定位置上
请把正确选项的代号填在答题卡指定位置上 ![]() )
)
1 ![]() 设集合
设集合![]() ,
,![]() ,
,![]() ,则
,则![]() =
( )
=
( )
A ![]()
![]() B
B ![]()
![]()
C ![]()
![]() D
D ![]()
![]()
2 ![]()
![]() = ( )
= ( )
A ![]()
![]() B
B ![]() 0 C
0 C ![]()
![]() D
D ![]()
![]()
3 ![]()
![]() 是虚数单位,
是虚数单位,![]() ( )
( )
A ![]()
![]() B
B ![]()
![]()
C ![]()
![]() D
D ![]()
![]()
4 ![]() 函数
函数![]() 的反函数的解析表达式为
( )
的反函数的解析表达式为
( )
A ![]()
![]() B
B ![]()
![]()
C ![]()
![]() D
D ![]()
![]()
5 ![]() 在各项都为正数的等比数列
在各项都为正数的等比数列![]() 中,首项
中,首项![]() ,前三项和为21,则
,前三项和为21,则![]() =( )
=( )
A ![]() 33
B
33
B ![]() 72
C
72
C ![]() 84
D
84
D ![]() 189
189
6 ![]() 如果
如果 是连续函数,则
是连续函数,则![]() 等于
( )
等于
( )
A ![]() 1
B
1
B ![]() -1 C
-1 C ![]() 0 D
0 D ![]() 2
2
7 ![]() 函数
函数![]() 的反函数的图象大致是 ( )
的反函数的图象大致是 ( )
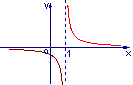
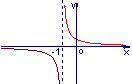
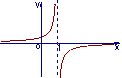
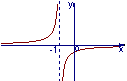
A ![]() B
B ![]() C
C ![]() D
D ![]()
8 ![]() 设
设![]() 是可导函数,且
是可导函数,且![]() ( )
( )
A ![]()
![]() B
B ![]() -1 C
-1 C ![]() 0 D
0 D ![]() -2
-2
9 ![]() 在一次歌手大奖赛上,七位评委为歌手打出的分数如下: 9
在一次歌手大奖赛上,七位评委为歌手打出的分数如下: 9 ![]() 4, 8
4, 8 ![]() 4, 9
4, 9 ![]() 4, 9
4, 9 ![]() 9, 9
9, 9 ![]() 6, 9
6, 9 ![]() 4, 9
4, 9 ![]() 7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为 ( )
7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为 ( )
A ![]() 9
9 ![]() 5, 0
5, 0 ![]() 04
B
04
B ![]() 9
9 ![]() 5, 0
5, 0 ![]() 016
016
C ![]() 9
9 ![]() 4, 0
4, 0 ![]() 484
D
484
D ![]() 9
9 ![]() 4, 0
4, 0 ![]() 016
016
10 ![]() 设
设![]() 是函数
是函数![]() 的反函数,则使
的反函数,则使![]() 成立的x的取值范围为 ( )
成立的x的取值范围为 ( )
A ![]()
![]() B
B ![]()
![]() C
C ![]()
![]() D
D ![]()
![]()
11 ![]() 设
设![]() ,则
,则![]() 的展开式中
的展开式中![]() 的系数不可能是
( )
的系数不可能是
( )
A ![]() 10
B
10
B ![]() 40
C
40
C ![]() 50
D
50
D ![]() 80
80
12 ![]() 若函数
若函数![]() 在区间
在区间![]() 内单调递增,则a的取值范围是 ( )
内单调递增,则a的取值范围是 ( )
A ![]()
![]() B
B ![]()
![]() C
C ![]()
![]() D
D ![]()
![]()
二 ![]() 填空题(本大题共4小题,每小题4分,共16分
填空题(本大题共4小题,每小题4分,共16分 ![]() 请把答案填在答题卡指定位置上.)
请把答案填在答题卡指定位置上.)
13 ![]() 曲线
曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是 ![]()
14 ![]() 函数
函数![]() 的定义域为
的定义域为 ![]()
15 ![]() 一工厂生产了某种产品16800件,它们来自甲
一工厂生产了某种产品16800件,它们来自甲 ![]() 乙
乙
![]() 丙3条生产线,为检查这批产品的质量,决定采用分层抽样的方法进行抽样,已知甲
丙3条生产线,为检查这批产品的质量,决定采用分层抽样的方法进行抽样,已知甲
![]() 乙
乙
![]() 丙三条生产线抽取的个体数组成一个等差数列,则乙生产线生产了 件产品
丙三条生产线抽取的个体数组成一个等差数列,则乙生产线生产了 件产品 ![]()
16
![]() 若等差数列
若等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,则当
,则当![]() 取最大值时
取最大值时![]() 的值为
的值为 ![]()
三 ![]() 解答题(本大题共6小题,共74分
解答题(本大题共6小题,共74分 ![]() 解答应写出文字说明
解答应写出文字说明
![]() 证明过程或演算步骤
证明过程或演算步骤
![]() )
)
17 ![]() (本题满分12分)已知数列
(本题满分12分)已知数列![]() 为等差数列,且
为等差数列,且![]()
![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)证明![]()
![]()
18 ![]() (本题满分12分)已知函数
(本题满分12分)已知函数![]() (a,b为常数)且方程
(a,b为常数)且方程![]() 有两个实根为
有两个实根为![]() ,
,![]()
![]()
(1)求函数![]() 的解析式;
的解析式;
(2)设![]() ,解关于x的不等式:
,解关于x的不等式:![]()
![]()
19 ![]() (本题满分12分)某城市有甲
(本题满分12分)某城市有甲 ![]() 乙
乙
![]() 丙3个旅游景点,一位客人游览这三个景点的概率分别是0
丙3个旅游景点,一位客人游览这三个景点的概率分别是0 ![]() 4,0
4,0 ![]() 5,0
5,0 ![]() 6,且客人是否游览哪个景点互不影响,设
6,且客人是否游览哪个景点互不影响,设![]() 表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值
表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值 ![]()
(1)求![]() 的分布及数学期望;
的分布及数学期望;
(2)记“函数![]() 在区间[2,+∞
在区间[2,+∞![]() 上单调递增”为事件A,
上单调递增”为事件A,
求事件A的概率.
20
![]() (本题满分12分)用总长14
(本题满分12分)用总长14 ![]() 8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0
8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0 ![]() 5m,那么高为多少时容器的容积最大?并求出它的最大容积.
5m,那么高为多少时容器的容积最大?并求出它的最大容积.
21 ![]() (本小题满分12分)已知
(本小题满分12分)已知![]() ,函数
,函数![]()
![]()
⑴当![]() 时,求使
时,求使![]() 成立的
成立的![]() 的集合;
的集合;
⑵求函数![]() 在区间
在区间![]() 上的最小值
上的最小值![]()
22 ![]() (本小题满分14分)设数列
(本小题满分14分)设数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,
,
且![]() ,其中A
,其中A ![]() B为常数
B为常数![]()
⑴求A与B的值;
⑵证明:数列![]() 为等差数列;
为等差数列;
⑶证明:不等式![]() 对任何正整数
对任何正整数![]() 都成立
都成立![]()
永安九中2005—2006学年度高三期中考试卷数学参考答案
一 ![]() 选择题
选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | A | D | A | C | A | B | B | B | A | C | B |
二 ![]() 填空题
填空题
13 ![]()
![]() 14
14 ![]()
![]() 15
15
![]() 5600 16
5600 16 ![]() 5
5
三 ![]() 解答题:
解答题:
17 ![]() (本题满分12分)
(本题满分12分)
(1)解:设等差数列![]() 的公差为d
的公差为d ![]()
由![]() 即d=1
即d=1 ![]() ……2分
……2分
所以![]() 即
即![]() ……6分
……6分
(2)证明因为![]() ,……8分
,……8分
所以![]()
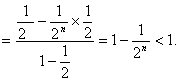 ……12分
……12分
18 ![]() (本题满分12分)
(本题满分12分)
(1)将![]() 得
得
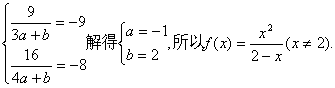 ……6分
……6分
(2)不等式即为![]()
即![]() ……8分
……8分
①当1<k<2时,解集(1,k)∪(2,+![]() );
);
②当![]()
③![]()
![]() ……12分
……12分
19 ![]() (本题满分12分)
(本题满分12分)
解:(1)分别记“客人游览甲景点”,“客人游览乙景点”,“客人游览丙景点”
为事件A1,A2,A3 ![]() 由已知A1,A2,A3相互独立,
由已知A1,A2,A3相互独立,
P(A1)=0 ![]() 4,P(A2)=0
4,P(A2)=0 ![]() 5, P(A3)=0
5, P(A3)=0 ![]() 6
6 ![]() ……2分
……2分
客人游览的景点数的可能取值为0,1,2,3 ![]() 相应地,客人没有游览的景点数的可能取
相应地,客人没有游览的景点数的可能取
值为3,2,1,0,所以![]() 的可能取值为1,3
的可能取值为1,3 ![]()
P(![]() =3)=P(A1·A2·A3)+ P(
=3)=P(A1·A2·A3)+ P(![]() )
)
= P(A1)P(A2)P(A3)+P(![]() )
)
=2×0 ![]() 4×0
4×0 ![]() 5×0
5×0 ![]() 6=0
6=0 ![]() 24,
24,
|
所以![]() 的分布列为
的分布列为
E![]() =1×0
=1×0 ![]() 76+3×0
76+3×0 ![]() 24=1
24=1 ![]() 48
48 ![]() ……6分
……6分
(2)解法一 因为![]()
所以函数![]() 上单调递增,……8分
上单调递增,……8分
要使![]() 上单调递增,当且仅当
上单调递增,当且仅当![]() ……10分
……10分
从而![]() ……12分
……12分
解法二:![]() 的可能取值为1,3
的可能取值为1,3 ![]() ……7分
……7分
当![]() =1时,函数
=1时,函数![]() 上单调递增,……9分
上单调递增,……9分
当![]() =3时,函数
=3时,函数![]() 上不单调递增
上不单调递增 ![]() ……11分
……11分
所以![]() ……12分
……12分
20 ![]() (本题满分12分)
(本题满分12分)
解:设容器底面短边长为x m,则另一边长为(x + 0 ![]() 5)m,高为
5)m,高为
![]() .……3分
.……3分
由3 ![]() 2 – 2x
> 0和x > 0,得0 < x < 1
2 – 2x
> 0和x > 0,得0 < x < 1 ![]() 6,……5分
6,……5分
设容器的容积为y m3,则有
y =
x (x + 0 ![]() 5)(3
5)(3 ![]() 2 – 2x) (0 < x < 1
2 – 2x) (0 < x < 1 ![]() 6).……7分
6).……7分
整理,得
y =
– 2x3 + 2 ![]() 2x2
+ 1
2x2
+ 1 ![]() 6x,
6x,
所以 ![]() + 4
+ 4 ![]() 4x + 1
4x + 1
![]() 6.
6.
令![]() = 0,有– 6x2 + 4
= 0,有– 6x2 + 4 ![]() 4x + 1
4x + 1
![]() 6 = 0,
6 = 0,
即 15x2 – 11x – 4 = 0,
解得 x1 =
1,x2 =![]() (不合题意,舍去).……10分
(不合题意,舍去).……10分
从而,在定义域(0,1 ![]() 6)内只有在x = 1处使
6)内只有在x = 1处使![]() = 0.由题意,若x过小(接近0)或过大(接近1
= 0.由题意,若x过小(接近0)或过大(接近1 ![]() 6)时,y值很小(接近0),因此,当x = 1时y取得最大值
6)时,y值很小(接近0),因此,当x = 1时y取得最大值
y最大 =
– 2 + 2 ![]() 2 + 1
2 + 1 ![]() 6 = 1
6 = 1 ![]() 8,
8,
这时,高为3 ![]() 2 – 2 × 1 = 1
2 – 2 × 1 = 1
![]() 2.
2.
答:容器的高为1 ![]() 2m时容积最大,最大容积为1
2m时容积最大,最大容积为1 ![]() 8m3.……12分
8m3.……12分
21 ![]() (本题满分12分)
(本题满分12分)
(1)由题意,![]()
当![]() 时,由
时,由![]() ,解得
,解得![]() 或
或![]() ;
;
当![]() 时,由
时,由![]() ,解得
,解得![]()
![]()
综上,所求解集为![]() ……4分
……4分
(2)设此最小值为![]()
![]()
①当![]() 时,在区间[1,2]上,
时,在区间[1,2]上,![]() ,
,
因为![]() ,
,![]() ,
,
则![]() 是区间[1,2]上的增函数,所以
是区间[1,2]上的增函数,所以![]()
![]()
②当![]() 时,在区间[1,2]上,
时,在区间[1,2]上,![]() ,由
,由![]() 知
知
![]()
![]()
③当![]() 时,在区间[1,2]上,
时,在区间[1,2]上,![]()
![]()
若![]() ,在区间(1,2)上,
,在区间(1,2)上,![]() ,则
,则![]() 是区间[1,2]上的增函数,
是区间[1,2]上的增函数,
所以![]()
![]()
若![]() ,则
,则![]()
当![]() 时,
时,![]() ,则
,则![]() 是区间[1,
是区间[1,![]() ]上的增函数,
]上的增函数,
当![]() 时,
时,![]() ,则
,则![]() 是区间[
是区间[![]() ,2]上的减函数,
,2]上的减函数,
因此当![]() 时,
时,![]() 或
或![]()
![]()
当![]() 时,
时,![]() ,故
,故![]() ,
,
当![]() 时,
时,![]() ,故
,故![]()
![]()
总上所述,所求函数的最小值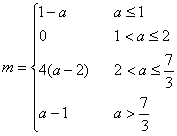
![]() ……12分
……12分
22 ![]() (本题满分14分)
(本题满分14分)
(1)由已知,得![]() ,
,![]() ,
,![]()
由![]() ,知
,知
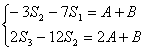 ,即
,即![]()
解得![]()
![]() ……4分
……4分
(2)由(1)得![]() ①
①
所以 ![]() ②
②
②-①得 ![]() ③
③
所以 ![]() ④
④
④-③得 ![]()
![]()
因为 ![]()
所以 ![]()
因为 ![]()
所以 ![]()
所以 ![]() ,
,![]()
又 ![]()
所以数列![]() 为等差数列
为等差数列![]() ……9分
……9分
(3)由(2)可知,![]() ,
,
要证 ![]()
只要证 ![]() ,
,
因为 ![]() ,
,
![]() ,
,
故只要证 ![]()
![]() ,
,
即只要证 ![]() ,
,
因为 ![]()
所以命题得证![]() ……14分
……14分