2005-2006学年度高安中学高三单元试题之一：
集合和简易逻辑 2005
9
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有
一项是符合题目要求的．
1．满足条件{1,2,3}
M{1,2,3,4,5,6}的集合M的个数是 （ ）
A．8 B．7 C．6 D．5
2．若命题P：x∈A∪B，则
P是
( )
A．x
A且xB B．xA或xB C．xA∩B D．x∈A∩B
3．定义A－B＝{xx∈A且xB}，若M＝{1,2,3,4,5}，N＝{2,3,6}，则N－M＝ （ ）
A．M B．N C．{1,4,5} D．{6}
4．“△ABC中，若∠C＝90°，则∠A、∠B都是锐角”的否命题是 （ ）
A．△ABC中，若∠C≠90°，则∠A、∠B都不是锐角
B．△ABC中，若∠C≠90°，则∠A、∠B不都是锐角
C．△ABC中，若∠C≠90°，则∠A、∠B都不一定是锐角
D．以上都不对
5．设集合A＝{xx<－1或x>1}，B＝{xlog2x>0}，则A∩B＝ ( )
A．{x x>1} B．{xx>0} C．{xx<－1} D．{xx<－1或x>1}
6．“若一个数不是负数，则它的平方不是正数”和这个命题真值相同的命题为 （ ）
A．若一个数是负数，则它的平方是正数B．若一个数的平方不是正数，则它不是负数
C．若一个数的平方是正数，则它是负数D．若一个数不是负数，则它的平方是非负数
7．若非空集合S
{1,2,3,4,5}，且若a∈S，则必有6－a∈S，则所有满足上述条件的集合S共有 （ ）
A．6个 B．7个 C．8个 D．9个
8．命题“若△ABC不是等腰三角形，则它的任何两个内角不相等”的逆否命题是（ ）
A．若△ABC是等腰三角形，则它的任何两个内角相等
B．若△ABC任何两个内角不相等，则它不是等腰三角形
C．若△ABC有两个内角相等，则它是等腰三角形
D．若△ABC任何两个角相等，则它是等腰三角形，
9．设有三个命题
甲：相交两直线m,n都在平面内，并且都不在平面内；
乙： m,n之中至少有一条与相交；
丙：与相交；
如果甲是真命题，那么 （ ）
A．乙是丙的充分必要条件 B．乙是丙的必要不充分条件
C．乙是丙的充分不必要条件 D．乙是丙的既不充分又不必要条件
10．有下列四个命题
①“若x＋y＝0，则x、y互为相反数”的逆命题；
②“全等三角形的面积相等”的否命题；
③“若q≤1，则x2＋2x＋q＝0有实根”的逆否命题；
④“不等边三角形的三个内角相等”的逆命题
其中真命题为 （ ）
A．①② B．②③ C．①③ D．③④
11．a1、b1、c1、a2、b2、c2均为非零实数，不等式a1x2＋b1x＋c1<0和a2x2＋b2x＋c2<0的解集分别为集合M和N，那么“
”是“M＝N” ( )
A．充分非必要条件 B．必要非充分条件
C．充要条件 D．既非充分又非必要条件
12．已知
，不等式
的解集是
，则
满足的关系是( )
A．
B．
C．
D．a、b的关系不能确定
二、填空题：本大题共4小题，每小题4分，共16分．答案填在题中横线上．
13．小宁中午放学回家自己煮面条吃 有下面几道工序：①洗锅盛水2分钟；②洗菜6分钟；③准备面条及佐料2分钟；④用锅把水烧开10分钟；⑤煮面条和菜共3分钟 以上各道工序，除④之外，一次只能进行一道工序 小宁要将面条煮好，最少要用________分钟
14．已知集合M＝{x1≤x≤10，x∈N}，对它的非空子集A，将A中每个元素k，都乘以(－1)k再求和(如A={1，3，6}，可求得和为(－1)·1＋(－1)3·3＋(－1)6·6＝2，则对M的所有非空子集，这些和的总和是 ．
15．设集合A＝{xx<4}，B＝{xx<1或x>3}，则集合{xx∈A且xA∩B}＝_______________
16．设集合A＝{xx2＋x－6＝0}，B＝{xmx+1=0}，则B
A的一个充分不必要条件是_______
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
17．（本小题满分12分）已知p：方程x2＋mx＋1＝0有两个不等的负实根，q：方程4x2＋4(m－2)x＋1＝0无实根 若p或q 为真，p且q为假 求实数m的取值范围
18．（本小题满分12分）已知
；¬
是¬
的必要不充分条件，求实数
的取值范围．
19．（本小题满分12分）已知关于x的不等式(k2＋4k－5)x2＋4(1－k)x＋3>0对任何实数x都成立，求实数k的取值范围
20．（本小题满分12分） 在一次数学竞赛中，共出甲、乙、丙三题，在所有25个参赛的学生中，每个学生至少解出一题；在所有没有解出甲题的学生中，解出乙题的人数是解出丙题的人数的两倍；只解出甲题的学生比余下的学生中解出甲题的学生的人数多1；只解一题的学生中，有一半没有解出甲题 问共有多少学生只解出乙题？
21．（本小题满分12分）设a、b∈Z，E＝{(x,y)(x－a)2＋3b≤6y}，点(2，1)∈E，但(1，0)
E，(3，2)E 求a、b的值
22．（本小题满分14分）已知集合M是满足下列性质的函数f(x)的全体：存在非零常数T，对任意x∈R，有f(x+T)=T f(x)成立．
⑴函数f(x)= x 是否属于集合M？说明理由；
⑵设函数f(x)=ax（a>0,且a≠1）的图象与y=x的图象有公共点，证明：f(x)=ax∈M；
⑶若函数f(x)=sinkx∈M ,求实数k的取值范围
高三单元试题之一：集合和简易逻辑参考答案
一、1．C 2．A 3．D 4．B 5．A 6．C 7．B 8．C 9．A 10．C 11．D 12．B
二、13．15 14． 2560 15． [1，3] 16． m=
(也可为m=
)
三、17．由题意p,q中有且仅有一为真，一为假，
p真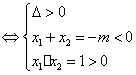
m>2，q真
<01<m<3,
若p假q真，则
1<m≤2；若p真q假，则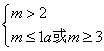
m≥3；
综上所述：m∈(1,2]∪[3，+∞)．
18．由
，得
，
∴¬即A=
；
由
得
，∴¬即B=
，
∵¬是¬的必要不充分条件，且m>0 ∴A
B，故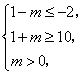
且不等式组中的第一、二两个不等式不能同时取等号，解得m≥9为所求
19．(1)当k2+4k－5＝0时，k=－5或k=1 当k=－5时，不等式变为24x+3+>0，显然不满足题意，∴k≠－5 当k=1时，不等式变为3>0，这时x∈R
(2)当k2+4k－5≠0，根据题意有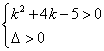
1<k<19
20．设解出甲、乙、丙三题的学生的集合分别为A、B、C，并用三个圆表示之，则重叠部分表示同时解出两题或三题的学生的集合，其人数分别以a,b,c,d,e,f,g表示
由于每个学生至少解出一题，故a+b+c+d+e+f+g=25 ①
由于没有解出甲题的学生中，解出乙题的人数是解出丙题的人数的2倍，故b+f=2(c+f) ②
由于只解出甲题的学生比余下的学生中解出甲题的学生的人数多1，故a=d+e+g+1 ③
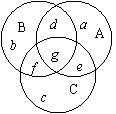由于只解出一题的学生中，有一半没有解出甲题，故a=b+c④
由②得：b=2c+f，f＝b－2c ⑤
以⑤代入①消去f得a+2b－c+d+e+g=25 ⑥
以③④代入⑥得：2b－c+2d+2e+2g=24 ⑦
3b+d+e+g=25 ⑧
以2×⑧－⑦得：4b+c=26 ⑨
∵c≥0,∴4b≤26，b≤6
利用⑤⑨消去c，得f=b－2(26－4b)＝9b－52
∵f≥0,∴9b≥52，b≥
∵b∈Z，∴b=6 即只解出乙题的学生有6人
21．∵点(2,1)∈E，∴(2－a)2+3b≤6 ①
∵点(1,0)E，∴(1－a)2+3b>0 ②
∵点(3,2)E，∴(3－a)2+3b>12 ③
由①②得6－(2－a)2>－(1－a)2，解得a>－
；类似地由①③得a<－
∴－<a<－
22．⑴对于非零常数T，f(x+T)=x+T, Tf(x)=Tx． 因为对任意x∈R，x+T=
Tx不能恒成立，∴f(x)=
⑵因为函数f(x)=ax（a>0且a≠1）的图象与函数y=x的图象有公共点，
所以方程组：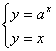
有解，消去y得ax=x,
显然x=0不是方程ax=x的解，所以存在非零常数T，使aT=T．
于是对于f(x)=ax有
故f(x)=ax∈M．
⑶当k=0时，f(x)=0，显然f(x)=0∈M．
当k≠0时，因为f(x)=sinkx∈M，所以存在非零常数T，对任意x∈R，有
f(x+T)=T f(x)成立，即sin(kx+kT)=Tsinkx ．
因为k≠0，且x∈R，所以kx∈R，kx+kT∈R，
于是sinkx ∈[－1，1]，sin(kx+kT) ∈[－1，1]，
故要使sin(kx+kT)=Tsinkx ．成立，
只有T=
，当T=1时，sin(kx+k)=sinkx
成立，则k=2mπ, m∈Z ．
当T=－1时，sin(kx－k)=－sinkx 成立，即sin(kx－k+π)= sinkx 成立，
则－k+π=2mπ, m∈Z ，即k=－2(m－1)π, m∈Z ．
综合得，实数k的取值范围是{kk= mπ,
m∈Z}