哈尔滨市第九中学2006届高三十月份月考试题
数学（理科）
第I卷
一
选择题：（本题共12小题，每小题5分，共60分 在每小题给出的四个选项中，只有一项是符合题目要求的）
1．设I为全集，S1 S2 S3是I的三个非空子集，且S1∪S2∪S3=I，则下面论断正确的是（ ）
A．C1S1∩(S2∪S3)=φ B．S1
（C1S2∩C1S3）
C．C1S1∩C1S2∩C1S3=φ D．S1（C1S2∪C1S3）
2．映射f：A→B，如果满足集合B中的任意一个元素在A中都有原象，则称为“满射” 已
知A中有4个元素，B中有3个元素，那么从A到B的不同满射的个数为 （ ）
A．24 B．6 C．36 D．72
3．函数
反函数是 （ ）
A．y=1+
(－1≤x≤1) B．y=1+(0≤x≤1)
C．y=1－(－1≤x≤1) D．y=1－(0≤x≤1)
4．
= （ ）
A．－
B． C．－
D．
5．计算机中常用十六进制是逢16进1的计数制，采用数字0~9和字母A~F共16个计数符
号，这些符号与十进制的数的对应关系如下表：
| 十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如：用十六进制表示：E+D=1B，则A×B=
A．6E B．72 C．5F D．B0
6．“m=”是“直线(m+2)x+3my+1=0与直线(m－2)x+(m+2)y－3=0相互垂直”的（ ）
A．充分必要条件 B．充分而不必要条件
C．必要而不充分条件 D．既不充分也不必要条件
7．若函数f(x)是定义在R上的偶函数，在
上是减函数，且f(2)=0，则使得f(x)<0的x
的取值范围是 （ ）
A．（－∞，2） B．（2，+∞）
C．（－∞，－2）∪（2，+∞） D．（－2，2）
8．若复数
为虚数单位）是纯虚数，则实数a的值为 （ ）
A．－2 B．4 C．－6 D．6
9．若函数
内单调递增，则a的取值范围
是 （ ）
A．
B．
C．
D．
10．函数f(x)=x3－3x2+1是减函数的区间为 （ ）
A．（2，+∞） B．（－∞，2） C．（－∞，0） D．（0，2）
11．函数
的值域是 （ ）
A．（1，+∞） B．（0，1） C．（0，+∞） D．（－∞，1）
12．在R上定义运算
：xy=x(1－y) 若不等式(x－a) (x+a)<1对任意实数x成立，则
A．－1<a<1 B．0<a<2 C．
D．
第Ⅱ卷
二 填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上
13．经问卷调查，某班学生摄影分别执“喜欢” “不喜欢”和“一般”三种态度，其中执“一般”态度的比“不喜欢”态度的多12人，按分层抽样方法从全班选出部分学生座谈摄影，如果选出的5位“喜欢”摄影的同学 1位“不喜欢”摄影的同学和3位执“一般”态度的同学，那么全班学生中“喜欢”摄影的比全班人数的一半还多 人
14．设y=f(x)是定义在R上的奇函数，且图象关于直线x=对称，则f(1)+f(2)+f(3)+f(4)+f(5)=
15．曲线y=x3在点(a,a3)(a≠0)处的切线与x轴 直线x=a所围成的三角形的面积为，则
a=
16．设函数y=f(x)的图象关于点（1，2）对称，且存在反函数f－1(x)，若f(4)=0，则f－1(4)=
三 解答题：本大题共6小题，共74分 解答应写出文字说明，证明过程或演算步骤
17．（本大题满分12分）
解不等式x+x2－1>1
18．（本大题满分12分）
9粒种子分种在3个坑内，每坑3粒，每粒种子发芽的概率为0 5，若一个坑内至少有1粒种子发芽，则这个坑不需要补种，若一个坑内的种子都没发芽，则这个坑需补种假定每个坑至多补种一次，每补种1个坑需10元，用ξ表示补种费用，写出ξ的分布列并求ξ的数学期望 （精确到0 01）
19．（本大题满分12分）
奇函数f(x)在其定义域（－1，1）上单调递增，且f(1－a)+f(1－a2)<0，求a的取值范围
20．（本大题满分12分）
已知函数f(x)=x2+2ax+1在区间[－1，2]上的最大值是4，求a的值
21．（本小题满分12分） 已知f(x)=(
)2(x≥0),又数列{an}(an>0)中，a1=2, 前n项和的公式Sn(n∈N)对所有大于1的自然数n都有Sn=f(Sn－1)
（I）求数列{an}的通项公式；
（II）若
22．（本小题共14分）
设函数f(x)在(－∞，+∞)上满足f(2－x)=f(2+x), f(7－x)=f(7+x)，且在闭区间[0，7]上，只有f(1)=f(3)=0
（I）试判断函数y=f(x)的奇偶数；
（II）试求方程f(x)=0在闭区间[－2005，2005]上的根的个数，并证明你的结论
数学（理科）参考答案
一 选择题：CCBAA BDCBD AC
二 填空题：13 3； 14 0； 15 ±1； 16
－2
三 解答题：
17．解：当x2－1≥0时，x+x2－1>1，解得x<－2或x>1
当x2－1<0时，x－x2+1>1，解得0<x<1
∴不等式的解集为{xx<－2或0<x<1或x>1}
18．解：某坑需补种的概率为
，不需补种的概率为
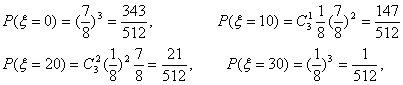
的分布列为：
| ξ | 0 | 10 | 20 | 30 |
| P |
|
|
|
|
∴Eξ=0×
+10×
+20×
+30×
=3 75
19．解：函数f(x)为奇函数，∴－f(1－a2)=f(a2－1) ，
∴f(1－a)<f(a2－1)，又f(x)在定域（－1，1）内是增函数
∴－1<1－a<a2－1<1，解得1<a<
20．解：函数f(x)是开口向上，对称轴为x=－a的抛物线，
当a≥－时4=f(2)=5+4a, ∴a=－
当a≥－时4=f(－1)=2－2a, ∴a=－1
21．解：
n≥2时an=Sn－Sn－1=4n－2, a1=2，数列{an}的通项公式为an=4n－2
22．解：函数f(x)在闭区间[0，7]上，只有f(1)=f(3)=0, ∴f(5)≠0
又f(2－x)=f(2+x), ∴f(－1)=f(5), ∴f(－1) ≠0，而∴f(1)=0
∴f(－1) ≠±f(1)，函数f(x)既不是奇函数也不是偶函数
由f(2－x)=f(2+x)得f(4－x)=f(x)
由f(7－x)=f(7+x)得f(4－x)=f(10+x), ∴f(x)=f(10+x)
10是函数f(x)的一个周期
而f(7－x)=f(7+x)，函数f(x)在[4，7]上无根，∴函数f(x)在[7，10]上无根
∴f(x)=0在[0，10]上恰有两根为1和3，f(x)=0的根为10n+1或10n+3的形式
解－2005≤10n+1≤2005得－200≤n≤200，共201个
解－2005≤10n+3≤2005得－200≤n≤200，共201个
∴方程f(x)=0在在闭区间[－2005，2005]上的根的个数为802