成都市2006届高中毕业班第一次诊断性检测题
数 学(文科)
天星教育网拥有制版权 侵权比究
参考公式:如果事件![]() 、
、![]() 互斥,那么
球的表面积公式
互斥,那么
球的表面积公式
![]() (
(![]() +
+![]() )=
)=![]() (
(![]() )+
)+![]() (
(![]() )
)
![]() =
=![]()
如果事件A、B相互独立,那么
其中![]() 表示球的半径
表示球的半径
![]() (
(![]() ·
·![]() )=
)=![]() (
(![]() )·
)·![]() (
(![]() )
球的体积公式
)
球的体积公式
如果事件![]() 在一次试验中发生的概率是
在一次试验中发生的概率是![]() ,
, ![]() =
=![]()
那么![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率 其中
次的概率 其中![]() 表示球的半径
表示球的半径
![]()
注意事项:全卷满分为150分,完成时间为120分钟.
天星教育网
第I卷(选择题,共60分)
一、选择题:本题共有12个小题,每小题5分;在每小题给出的四个选项中,只有一项是符合题目要求的,把正确选项的代号涂在机读卡的指定位置上.
1.![]() 的值为
的值为
(A)-3 (B)-1 (C)1 (D)3
2.若![]()
![]() ,则下列不等式中总成立的是
,则下列不等式中总成立的是
(A)![]() (B)
(B)![]()
![]() (C)
(C)![]()
![]() (D)
(D)![]()
3.设![]() 或
或![]() ,
,![]() 或
或![]() ,则
,则![]() 是
是![]() 的
的
(A)充分但不必要条件 (B)必要但不充分条件
(C)充要条件 (D)既不充分也不必要条件
4.已知![]() 是
是![]() 上的增函数,若令
上的增函数,若令![]() ,则
,则![]() 是
是![]() 上的
上的
(A)增函数 (B)减函数
(C)先减后增的函数 (D)先增后减的函数
5.已知直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,有下列四个命题:
,有下列四个命题:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中真命题是
(A)①② (B)③④ (C)②④ (D)①③
6.将函数![]() 的图象按向量
的图象按向量![]() 平移后得到函数
平移后得到函数![]() 的图象,则向量
的图象,则向量![]() 可以是
可以是
(A)(![]() ,0) (B)(
,0) (B)(![]() ,0) (C)(
,0) (C)(![]() ,0) (D)(
,0) (D)(![]() ,0)
,0)
7.一组数据,容量为150.按从小到大的组序分成10个组,其频数如下表:
| 组号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 频数 | 15 | 17 | 14 | 18 |
| 13 | 19 | 16 | 12 | 11 |
那么,第5组的频率为
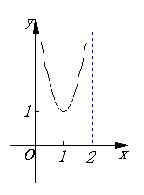 (A)0.1 (B)10
(C)0.15
(D)15
(A)0.1 (B)10
(C)0.15
(D)15
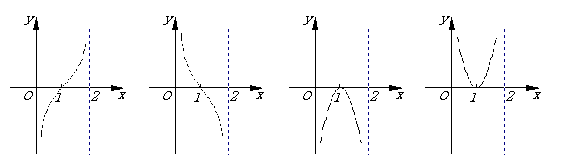 8.函数
8.函数![]()
![]() 的图象如右图所示,则
的图象如右图所示,则![]() 的示意图是
的示意图是
(A) (B) (C) (D)
9.设向量![]() (
(![]() ,
,![]() ),
), ![]() (
(![]() ,
,![]() ),若
),若![]() 是实数,且
是实数,且![]() ,则
,则![]() 的最小值为
的最小值为
(A)![]() (B)1
(C)
(B)1
(C)![]() (D)
(D)![]()
10.有A、B、C、D、E、F 6个集装箱,准备用甲、乙、丙三辆卡车运送,每台卡车一次运两个.若卡车甲不能运A箱,卡车乙不能运B箱,此外无其它任何限制条件;要把这6个集装箱分配给这3台卡车运送,则不同的分配方案的种数为
(A)168 (B)84 (C)56 (D)42
11.已知![]() -
-![]() ,则
,则![]()
![]()
![]() =
=
(A)![]() (B)
(B)![]() (C)1
(D)0
(C)1
(D)0
12.已知![]() ,
,![]() 满足
满足![]()
![]() ,则
,则![]() 与
与![]() 的关系为
的关系为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
天星教育网
第II卷(非选择题,共90分)
二.填空题:(本大题共4小题,每小题4分,共16分)把答案填在题中横线上.
 13.
13.![]() 的展开式中,
的展开式中,![]() 的系数为_______________________(用数字作答).
的系数为_______________________(用数字作答).
14.在数列![]() 和
和![]() 中,
中,![]() 是
是![]() 和
和![]() 的等差中项,
的等差中项,![]() 且对任意
且对任意![]() 都有
都有![]() ,则
,则![]() 的通项
的通项![]() =_______________________________________.
=_______________________________________.
15.若角![]() 、
、![]() 满足
满足![]() ,则
,则![]() 的取值范围是_______________________________.
的取值范围是_______________________________.
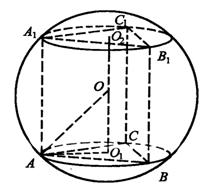
16.如图,棱长为3的正三棱柱内接于球![]() 中,则球
中,则球![]() 的表面积为_____________________.
的表面积为_____________________.
三.解答题:(本大题共6小题,共74分)解答应写出文字说明、证明过程或推演步骤.
17.(共12分)天星教育网
甲、乙两人参加一项智力测试.已知在备选的10道题中,甲能答对其中的6道题,乙能答对其中的8道题.规定每位参赛者都从备选题中随机抽出3道题进行测试,至少答对2道题才算通过.
(1)求甲答对试题数![]() 的概率分布及数学期望;
的概率分布及数学期望;
(2)求甲、乙两人至少有一人通过测试的概率.
18.(共11分)
已知![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边分别是
所对的边分别是![]() 、
、![]() 、
、![]() ,
,![]()
![]()
![]()
![]() 且
且![]() =
=![]() .求
.求![]() 的值.
的值.
19.(共14分)
如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,且
为正方形,且![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1) 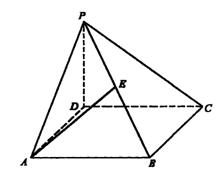 求异面直线
求异面直线![]() 、
、![]() 所成的角;
所成的角;
(2) 在平面![]() 内求一点
内求一点![]() ,使得
,使得![]() 平面
平面![]() ;
;
(3) 求二面角![]() 的大小.
的大小.
20.(共12分)
已知向量![]() ,
,![]() ,
,![]() 、
、![]() 为正实数,
为正实数,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的最大值;
的最大值;
(2)是否存在![]() 、
、![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
21.(共12分)
某西部山区的某种特产由于运输原因,长期只能在当地销售,当地政府对该项特产的销售投资收益为:每投入![]() 万元,可获得利润
万元,可获得利润![]() 万元.当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划前后对该项目每年都投入60万元的销售投资,在未来10年的前5年中,每年都从60万元中拨出30万元用于修建一条公路,5年修成,通车前该特产只能在当地销售;公路通车后的5年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每投入
万元.当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划前后对该项目每年都投入60万元的销售投资,在未来10年的前5年中,每年都从60万元中拨出30万元用于修建一条公路,5年修成,通车前该特产只能在当地销售;公路通车后的5年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每投入![]() 万元,可获利润
万元,可获利润![]() 万元.问从10年的累积利润看,该规划方案是否可行?
万元.问从10年的累积利润看,该规划方案是否可行?
22.(共13分)
已知数列![]() 中,
中,![]() (
(![]() =1,2,3,…),其前
=1,2,3,…),其前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,
,![]() 且
且![]() .数列
.数列![]() 满足
满足![]() .
.
(I)求数列![]() 、
、![]() 的通项
的通项![]() 与
与![]() ;
;
(II)若![]() ,记
,记![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]()
![]()
![]() .
.
成都市2006届高中毕业班第一次诊断性检测题
数学试题(文科)参考答案及评分意见
1. D 2. B 3. A 4. B 5. D 6. B 7. A 8. C 9. C 10. D
11. A 12. D天星教育网
13.设![]() 由
由![]() 。
。![]() 的系数为
的系数为![]() 。
。
14.![]() 。
。![]() 是公比为
是公比为![]() 的等比数列
的等比数列![]()
![]() 。
。
15.![]() 又
又
![]() 即
即![]() 。
。
[注]:只有左界者得1分。
16.可求得![]() 设该球的半径为R,则AO=R。由
设该球的半径为R,则AO=R。由![]() +
+
![]() ,得
,得![]() 。
。
17.解:(I)设甲、乙两人通过测试的事件分别为A、B,则
![]() ,
2分
,
2分
![]() 。
2分
。
2分
∵A、B相互独立,
∴甲、乙两人都通过测试的概率为
![]() 。
3分
。
3分
(II)∵A、B相互独立,
∴甲、乙两人都通过测试的概率为
![]() 。
3分
。
3分
∴甲、乙两人至少有一人通过测试的概率为
![]() 。
2分
。
2分
18.解:由![]() 有
有
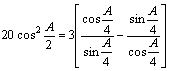 ,
2分
,
2分
即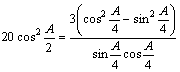 。
。
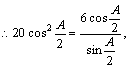 2分
2分
即![]() 。
。
![]() 。
1分
。
1分
∵A、B、C是三角形的内角,![]() ,
,
![]() 。
2分
。
2分
又∵b<a<c,∴A为锐角。
![]() 。
2分
。
2分
![]() 。
2分
。
2分
19.解:(1)建立如图所示的空间直角坐标系,则A (a,0,0) , B(a,a,0),
C(0,a,0),P(0,0,a)
![]() 。
。
![]()
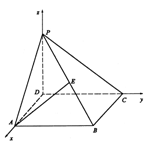
![]() 。
。
![]() 。
。
又![]()
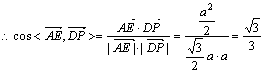 。
。
故异面直线AE、DP所成角为![]() 。
7分
。
7分
(II)∵F∈平面PAD,故设F(x,0,z),则有![]() 。
。
∵EF⊥平面PBC,∴![]() 且
且![]() 。
。
∴![]()
又![]() ,
,
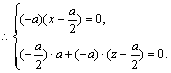
从而![]()
∴![]() ,取AD的中点即为F点。
7分
,取AD的中点即为F点。
7分
20.解:![]()
![]() 。
2分
。
2分
(1)若![]() 则
则![]() 。
。
![]() 。
2分
。
2分
整理,得![]()
![]() 3分
3分
(2)假设存在正实数k、t,使![]() ,则
,则
![]() 。
2分
。
2分
化简,得![]() 。
2分
。
2分
![]() 、t是正实数,故满足上式的k、t不存在。
、t是正实数,故满足上式的k、t不存在。
∴不存在这样的正实数k、t,使![]() 。
1分
。
1分
21.解:在实施规划前,由题设![]() (万元),知每年只须投入40万,即可获得最大利润100万元。
(万元),知每年只须投入40万,即可获得最大利润100万元。
则10年的总利润为W1=100×10=1000(万元)。 3分
实施规划后的前5年中,由题设![]() 知,每年投入30万元时,有最大利润
知,每年投入30万元时,有最大利润![]() (万元)。
(万元)。
前5年的利润和为![]() (万元)。
3分
(万元)。
3分
设在公路通车的后5年中,每年用x万元投资于本地的销售,而用剩下的(60-x)万元于外地区的销售投资,则其总利润为
![]()
![]() 。
3分
。
3分
当x=30时,W2max=4950(万元)。
从而10年的总利润为![]() (万元)。
2分
(万元)。
2分
![]() ,故该规划方案有极大实施价值。
1分
,故该规划方案有极大实施价值。
1分
22.解:(1)n=1时,![]() 由
由![]() 。
1分
。
1分
当n≥2时
![]() ①
①
![]() ②
②
由②—①,有![]() 2分
2分
从而,![]() 。
。
∴数列![]() 是以1为首项,
是以1为首项,![]() 为公比的等比数列。
为公比的等比数列。
∴![]() 。
3分
。
3分
∴ ![]() 1分
1分
(2)当![]() 时,
时,![]() 。
1分
。
1分
![]() 。
。
∵![]() ③
③
![]() 。
④
。
④
由③—④,得![]()
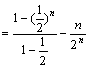 2分
2分
![]()
![]() 。
。
![]() 。
1分
。
1分
![]()
![]() 。
1分
。
1分