成都市2006届高中毕业班摸底测试
数学（理科）
第工卷（选择题，共60分）
一、选择题：
1．若集合A＝｛一1，0，1｝，集合B＝｛1，2，3｝，则集合AUB应表示为
(A）｛1｝ （B）｛一1，0｝
（C）｛0，1，2，3｝ （D）｛0，一1，1，2，3｝
2.已知Slnα=－
，
，则sin2α的值为（ ）
3.已知正项等比数列｛an｝中,a2·as·a８=64,a3=2，则数列｛aｎ｝的公比为
4.函数
的大致图象是（ ）
5.某交往式计算机有20个终端，这些终端由各个单位独立操作，使用率均为0.8,则个终端中至少有一个没有使用的概率为
(A）0.2 ２０（B）0.8 ２０（C）1一0.8２０（D）1－0.2 ２０
6.已知∆ABC中，
，则∆ABC的面积是（ ）
(A) 6 (B)
(C) 3 (D)
7.已知椭圆的方程为2ｘ２＋3ｙ２=m(m>0），则此椭圆的离心率为 （ ）
Ａ、
Ｂ、
Ｃ、
Ｄ、
8.若直线a∥平面α,则直线a与平面α内的直线的关系是
(A）平面a内有且仅有一条直线与α平行
（B）平面a内任意一条直线与直线α平行
(C)平面a内与直线a共面的直线与直线α平行
(D）以上都不对刀牙
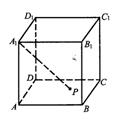
9.如图，Ｐ为正方体AＣ１的底面ABCD内任意一点，若Ａ１Ｐ与棱ＡＡ、ＡＢ、ＡＤ所成的角分别为α、β、γ,则 sinα+sinβ+ sinγ的值为（ ）
（A) 2 (B)1 (C）0 （D）随P的变化而变化
10.下列不等式中解集为实数集R的是（ ）
(A) x２＋4x+4>0 （B）
＞0
(C）
(D)x２－x+1>0
11.已知抛物线ｙ２=4ｘ及点A(l,l),若过点A的直线被此抛物线截得的弦ＰQ恰以Ａ为中点，则直线ＰQ的方程为（ ）
（A）4x－ｙ一3＝0 （B）2ｘ一ｙ＋1＝0 （C）4x－ｙ十3＝0 （D）2x－ｙ一1＝0
12.若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“孪生函数”，那么函数解析式为y=2ｘ２＋1，值域为｛5,19｝的“孪生函数”共有（ ）
(A) 10个 (B) 9个 (C) 8个 (Ｄ)7个
第Ⅱ卷（非选择题，共90分）
二、填空题：（本大题共4小题，每小题5分，共20分）把答案填在题中横线上．
13. 
展开式中各项系数之和为
14.直线
被圆(x-1)2+(y+2)2=4所截得的弦长为
．
15.双曲线
按向量
平移后的双曲线方程为
，则平移向量=
16.给出以下命题:①已知命题p、q，若“p或q”为真, “p且q”为假；②已知平面α、β均垂直于平面γ，α∩γ=a，β∪γ=b，则α⊥β的充要条件是a⊥b，③若函数f(x)为偶函数，则必有f(一x)=f(x)=f(x）恒成立．
其中正确命题的番号是 ．
三、解答题：（本大题共6小题，共70分）解答应写出文字说明、证明过程或推演步骤．
17.（共10分）已知函数f (x) =sin(x+ 6)+sin(x+
)+cosx+a，(a∈R ,a为常数)
（I）求函数f(x)的最小正周期；
（Ⅱ）若函数f(x)在〔
〕上的最小值为一1，求实数a的值。
18.（共10分）
一纸箱中放有除颜色外，其余完全相同的黑球和白球，其中黑球2个，白球3个．
（Ⅰ）从中同时摸出两个球，求两球颜色恰好相同的概率；
（Ⅱ）从中摸出一个球，放回后再摸出一个球，求两球颜色恰好不同的概率．
19.（共12分）
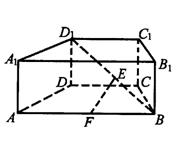
如图，直四棱柱ABCD-A1 B1 C1 D1中，底面ABCD是等腰梯形，AB∥ CD, AB = 2AD=2DC=2,E为BD1的中点，F为AB的中点．
（I）求证：EF∥平面ADD1A1；
（Ⅱ）若BB1=
求A1F与平面DEF所成的角的大小．
20.(共12分)
已知函数f(t)=log2t,t∈[
,8]．
（Ⅰ）求f(t)的值域G；
（Ⅱ）若对于G内的所有实数x，不等式
恒成立，求实数m的取值范围．
21.（共13分）
已知等差数列｛an｝中,al=l，公差d>0,且a2.a5.a14分别是等比数列｛bn｝的第二项、第三项、第四项．
（I）求数列｛an｝、（bn｝的通项an、 bn；
（Ⅱ）设数列｛cn｝对任意的n∈N*，均有
成立，求Cl +c2＋…＋C2005的值．
22.（共13分）
设向量
，且
0<m<3,x>0,y∈R．
（I）求动点p（x，y）的轨迹C的方程；
（Ⅱ）过点A(-1,0)作直线y=(x-2)/3与点P的轨迹交于B、C两点，问是否存在实数m使得
？若存在，求出m的值；若不存在，请说明理由．
