2004年江苏省 第二轮复习《不等式》专题
一、考纲要求
(1)理解不等式的性质及其证明。
(2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用。
(3)掌握分析法、综合法、比较法证明简单的不等式。
(4)掌握简单不等式的解法。
(5)理解不等式 a-b≤a+b≤a+b。
二、再现性题组
1、 选择
①不等式![]() ≥0的解集是
( )
≥0的解集是
( )
A.{x x<-2或x>2} B.{x x<-2或-1≤x≤1或x>2}
C.{x x<-2或x≥1} D.{x x≤-1或x>2}
②若log a![]() <1,则
( )
<1,则
( )
A.0<a<![]()
![]() B.
B.![]() <a<1 C.0<a<
<a<1 C.0<a<![]() 或a>1 D.a>
或a>1 D.a>![]()
③若a>0,b>0,则不等式a>![]() >-b的解集为
( )
>-b的解集为
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
④已知:M={x3-x≥![]() },N={xx2-(a+1)x+a≤0},当M
},N={xx2-(a+1)x+a≤0},当M![]() N时a的取值范围是( )
N时a的取值范围是( )
A.a≥1 B.1<a<2 C.a>2 D.a≥2
⑤若![]() ,则S=x2+y2有
( )
,则S=x2+y2有
( )
A. 最小值0,最大值16 B.
最小值![]() ,最大值4
,最大值4
C. 最小值0,最大值1 D. 最小值1,最大值16
⑥若不等式![]() ,对x∈R恒成立,则正整数k的值为
( )
,对x∈R恒成立,则正整数k的值为
( )
A.1 B.2 C.3 D.4
2、 填空
① 若不等式(a-2)x2+2(a-2)x-4<0对一切实数x都成立,
则a的取值范围是
② 若不等式(m2+4m-5)x2-4(m-1)x+3>0对一切实数x恒成立,
则m的取值范围是
③ 函数y=2x2-mx+3,当x∈![]() 时是增函数,则m的取值范围是
时是增函数,则m的取值范围是
④ 若x,y∈R+且xy-(x+y)=1,则x+y的最小值是
⑤不等式![]() 的解集是(-2,4),则实数a的值为
的解集是(-2,4),则实数a的值为
⑥若![]() 的解集是
,x-1+x-2>3的解集是
的解集是
,x-1+x-2>3的解集是
2<x+1≤5 的解集是
⑦若不等式x-2+ x+1<a的解集不是空集,则a∈
x-2-x+1>a的解集是空集,则a∈
⑧若x1,x2是关于x的方程7x2-(k+13)x+k2-k-2=0的两根,且0<x1<1<x2<2,求k的范围
⑨f(x)是关于x的一次函数,若1≤f(1)≤2,3≤f(2)≤4,则f(3)的取值范围是
⑩已知关于x的不等式ax2+bx+c<0的解集为{xx<α或x>β}其中α<β<0,
那么不等式cx2-bx+a>0的解集是
⑾不等式![]() 的解集为
的解集为![]() ,那么
,那么![]() 的值等于___ 答案
的值等于___ 答案![]()
3、 解不等式
①x4-4x3+x2+6x<0
②![]() ≥1
≥1
③![]() ≥0 ④
≥0 ④![]() ⑤
⑤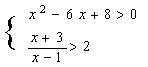
三.示范性题组
1、解关于x的不等式 ①![]() ②
②![]()
③![]() ④
④![]() , 其中
, 其中![]()
备课说明:本小题主要考查分式不等式的解法,考查分类讨论的数学思想
解:(1)原不等式可化为![]() 即
即![]()
∵a<1,∵(x-2)![]() 当
当![]() 时,即0<a<1时,解集为
时,即0<a<1时,解集为![]()
当![]() 时,即a=0时,解集为
时,即a=0时,解集为![]() ;
;
当![]() 时,即a<0时,解集为
时,即a<0时,解集为![]()
(2)原不等式的解集是下面不等式组(Ⅰ)、(Ⅱ)的解集的并集:
(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
分情况讨论
(i)当a<0或a>1时,有a<a2,此时不等式组(I)的解集为![]() 不等式组(II)的解集为空集φ;
不等式组(II)的解集为空集φ;
(ii)当![]() 时,有a2<a,此时,不等式组(I)的解集为空集φ,不等式组(II)的解集为
时,有a2<a,此时,不等式组(I)的解集为空集φ,不等式组(II)的解集为
![]()
(iii)当a=0或a=1时,原不等式无解.
综上,当a<0或a>1时时,原不等式的解集为![]() 当
当![]() 时,原不等式的解集为
时,原不等式的解集为![]() 当a=0或a=1时,原不等式的解集为φ
当a=0或a=1时,原不等式的解集为φ
(3).①若![]() ;
;
②若![]() ;
;
③若![]() 。
。
(4)解:![]()
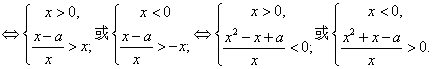
![]()
解![]() .
.![]()
![]() ,
,![]() 的解集是
的解集是![]() ;
;
![]() 的解集是
的解集是![]() ; 解
; 解![]() .
.![]()
![]() >0,
>0,
![]() 的解集是
的解集是![]()
![]() 的解集是
的解集是![]()
所以,原不等式的解集为: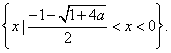
2、已知f(x)=log![]() (a>0,a≠1)
(a>0,a≠1)
1.求f(x)的定义域;
2.若f(x)>0,求x的取值范围
答案(1)(-1,1) (2)a>1时x∈(0,1) 0<a<1时x∈(-1,0)
3、若f(x)在定义域(-1,1)内可导,且f′(x)<0;又当a,b∈(-1,1)且a+b=0时,f(a)+f(b)=0,解不等式![]() 。
。
3、解:∵f(x)在(-1,1)内可导,且![]()
∴![]() 在(-1,1)上为减函数
在(-1,1)上为减函数
又当![]() ,a+b=0时,
,a+b=0时,![]()
∴![]() ,即
,即![]() ,即
,即![]()
∴f(x)在![]() 上为奇函数
上为奇函数
∴ ![]()

4、某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为G(x)(万元),其中固定成本为2万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本);销售收入R(x)(万元)满足:
 ,
,
假定该产品产销平衡,那么根据上述统计规律。
(1)要使工厂有赢利,产量x应控制在什么范围?
(2)工厂生产多少台产品时,可使赢利最多?
(3)求赢利最多时每台产品的售价。
4、依题意,![]() .设利润函数为f(x),则
.设利润函数为f(x),则
(1)要使工厂有赢利,即解不等式![]() ,当
,当![]() 时,
时,
解不等式![]() 。
。
即![]() .
.
∴1<x<7,∴![]() 。
。
当x>5时,解不等式![]() ,
,
得![]() 。 ∴
。 ∴![]() 。
。
综上,要使工厂赢利,x应满足1<x<8.2,
即产品应控制在大于100台,小于820台的范围内。
(2)![]() 时,
时,![]() ,故当x=4时,f(x)有最大值3.6.(8分)而当x>5时,
,故当x=4时,f(x)有最大值3.6.(8分)而当x>5时,![]() 所以,当工厂生产400台产品时,赢利最多.
所以,当工厂生产400台产品时,赢利最多.
(3)即求x=4时的每台产品的售价.此时售价为![]() (万元/百台)=240元/台.
(万元/百台)=240元/台.
5、如图所示,一过路人在河岸边行走,当走到A点时,突然听到河中B处有一落水儿童高喊“救命”。假设过路人在岸上跑步速度为0.3km/分,而在水中游泳速度为0.1km/分。试问过路人应该从哪一点入水,才能以最短的时间赶到落水地点?并说明理由(救护过程视B点为不动点)
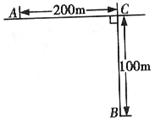
5、解:假设从D点入水,设![]() ,
,![]() ,
,
则过路人走完路程ADB所需的时间为(单位分钟)
![]()
化简得![]()
∵![]()
![]()
![]() 又t>0。
又t>0。
∴ ![]() 当
当![]() 时,a=165m
时,a=165m
即从D点入水赶到B点所用时间为![]() 分钟;若从A点入水赶到B点所用时间为
分钟;若从A点入水赶到B点所用时间为![]() ;若从C点入水赶到B点所用时间为
;若从C点入水赶到B点所用时间为![]() 分钟(11分);
分钟(11分);
∵![]() 所以过路人应从图中的D点入水,才能最短的时间赶到落水地点。
所以过路人应从图中的D点入水,才能最短的时间赶到落水地点。
6、某公司欲建连成片的网球场数座,用128万元购买土地10000平方米,该球场每座的建设面积为1000平方米,球场的总建筑面积的每平方米的平均建设费用与球场数有关,当该球场建x个时,每平方米的平均建设费用用f(x)表示,且f(n)=f(m)(1+![]() )(其中n>m,n∈N),又知建五座球场时,每平方米的平均建设费用为400元,为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和),公司应建几个球场?
)(其中n>m,n∈N),又知建五座球场时,每平方米的平均建设费用为400元,为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和),公司应建几个球场?
6、解:设建成x个球场,则每平方米的购地费用为![]() =
=![]()
由题意知f(5)=400, f(x)=f(5)(1+![]() )=400(1+
)=400(1+![]() )
)
从而每平方米的综合费用为y=f(x)+![]() =20(x+
=20(x+![]() )+300≥20.2
)+300≥20.2![]() +300=620(元),当且仅当x=8时等号成立
+300=620(元),当且仅当x=8时等号成立
故当建成8座球场时,每平方米的综合费用最省.
7、已知函数![]() 在R上是增函数,
在R上是增函数,![]() 。
。
(1)
求证:如果![]() ;
;
(2) 判断(1)中的命题的逆命题是否成立?并证明你的结论;
(3)解不等式![]() 。
。
7、证明:(1)当![]()
![]()
(2)(1)中命题的逆命题为:![]() ①
①
①的逆否命题是:![]() ②
②
仿(1)的证明可证②成立,又①与②互为逆否命题,故①成立,即(1)中命题的逆命题成立。
(1) 根据(2),所解不等式等价于
![]() 。
。
8、奇函数![]() 上是增函数,当
上是增函数,当![]() 时,是否存在实数m,使
时,是否存在实数m,使![]() 对所有的
对所有的![]() 均成立?若存在,求出适合条件的所有实数m;若不存在,说明理由。
均成立?若存在,求出适合条件的所有实数m;若不存在,说明理由。
8、解:易知![]() ,
,
![]()
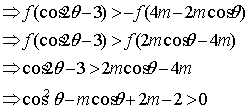

因此,满足条件的实数m存在,它可取![]() 内的一切值。
内的一切值。
9、某公司取消福利分房和公费医疗,实行年薪制工资结构改革.该公司从2003年起,每人
的工资由三个项目组成,并按下表规定实施:
| 项 目 | 金额(元/人,年) | 计 算 方 法 |
| 基础工资 | 10000 | 考虑物价因素,从2003年(含2003年)起每年递增10%(与工龄无关) |
| 住房补贴 | 400 | 按职工到公司年限计算,每工作一年补贴400元 |
| 医 疗 费 | 1600 | 固定不变 |
如果该公司今年年初有5位职工,计划从明年起每年年初新招5名职工.
(1)若今年(2003年)算第一年,试把第n年该公司付给职工工资总额y(万元)表示成年限n的函数;
(2)试判断公司每年发给职工的工资总额中,住房补贴和医疗费的总和能否超过基础工资总额的20%,请说明理由.
9、解:(1)依题意:第n年共有5n个职工,那么基础工资总额为![]() (万元),
(万元),
医疗费总额为5n×0.16=![]() (万元),
(万元),
住房补贴为5×0.04n+5×0.04(n-1)+……+5×0.04×2+5×0.04=5×0.04(1+2+3+…+n)
=0.2×![]() (万元).
(万元).
∴![]()
(2)假设可以超过,则![]()
即![]()
由函数![]() 的图象知,上面不等式不能成立.
的图象知,上面不等式不能成立.
故住房补贴和医疗费总和不会超过基础工资总额的20%.
四、巩固性题组
1、已知f(x)=lg(x+1),g(x)=2lg(2x+t)(t∈R,是参数),
(1)当t=-1时,解不等式f(x) ≤g(x);
(2)如果当x∈[0,1]时,f(x)≤g(x)恒成立,求参数t的取值范围。
1、解:(1)![]() 时,
时,![]() 即为
即为![]() ,
,
此不等式等价于
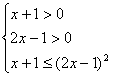 即
即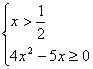 即
即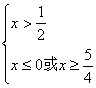
∴![]()
∴原不等式的解集为![]() .
.
(2)![]() 时,
时,![]() 恒成立。
恒成立。
∴![]() 时,
时,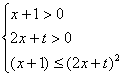 恒成立,∴
恒成立,∴![]() 时,
时,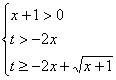 恒成立,
恒成立,
即![]() 时,
时,![]() 恒成立,于是转化为求
恒成立,于是转化为求![]() ,
,
![]() 的最大值问题,令
的最大值问题,令![]() ,则
,则![]() ,由
,由![]() ,知
,知![]()
∴![]() 。
。
当u=1即x=0时,![]() 有最大值1,∴t的取值范围是
有最大值1,∴t的取值范围是![]() 。
。
2、设向量![]() 。
。
(1)求![]() ;
;
(2)求![]() 的模的最小值。
的模的最小值。
2、解:由题![]() ,
,![]()
(1)![]()
(2)![]()
![]()
∴![]()
![]() ∴ 当
∴ 当![]() 时,
时,![]()
3、已知关于x的方程![]() 有一根是2.
有一根是2.
(1)
求实数a的值;(2)若![]() ,求不等式
,求不等式![]() 的解集.
的解集.
3、(1)用x=2代入原方程得![]()
![]()
(2)![]() ,则原不等式化为
,则原不等式化为![]() ,
,
解之得![]() ,即解集为
,即解集为![]()
![]()
4、某厂家拟在2004年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x万件与年促销费用m万元(![]() )(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件。已知2004年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。
)(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件。已知2004年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。
(1)将2004年该产品的利润y万元表示为年促销费用m万元的函数;
(2) 该厂家2004年的促销费用投入多少万元时,厂家的利润最大?
4、解:(1)由题意可知当![]()
每件产品的销售价格为![]()
∴2004年的利润![]()
![]()
(2)![]() ,
,
![]() (万元)答:(略)
(万元)答:(略)