2005—2006学年度福建省福州三中高三年级阶段测试
数 学 试 卷（文）
一、选择题：（共60分）
1．已知集合
，集合
，则
集合
为 （ ）
A．
B．
C．
D．
2．函数
的值域是 （ ）
A．
B． C．
D．
3．函数
的反函数是 （ ）
A．
B．
C．
D．
4．化简
得 （ ）
A．
B．
YCY C．－ D．－
5．在各项均为正数的等比数列
中，
的值为（ ）
A．112 B．84 C．56 D．28
6．已知等差数列
的值是 （ ）
A．10 B．9 C．8 D．7
7．已知函数
，则
的单调增区间是 （ ）
A．
B．
C．
D．
8．若关于
的不等式
有实数解，则b的取值范围是 （ ）
A．
B．YCY C． D．
9．已知数列的通项
，则此数列的最大项为 （ ）
A．第5项 B．第6项
C．第5或第6项 D．不存在
10．定义在R上的函数既是偶函数又是周期函数，若的最小正周期为
，且当
时，
的值为 （ ）
A．
B．
C．
D．
11．一个工厂生产某种产品480件，它们来自甲、乙、丙3条生产线，为检查这批产品的质
量，决定采用分层抽样的方法进行抽样，已知从甲、乙、丙3条生产线抽取的个体数组
成一个等差数列，则乙生产线生产的产品个数是YCY （ ）
A．160 B．180 C．240 D．无法确定
|
的图象如右图所示，
若
，
则M与N的大小关系是 （ ）
A．
B．
C．
D．
二、填空题：（共16分）
13．已知点
在直线
上，则
的值为 .
14．数列的前n项和为
，若
，则
.
15．垂直于直线
且与曲线
相切的直线方程是
.
16．已知
，则不等式
的解集为
.
三、解答题：（共74分）
17．（12分）已知
，
求
的值.
18．（12分）已知二次函数
的图象与轴交于A、B两点，且AB=4，它在y轴上
的截距为－3. 又对任意的都有
.
（1）求二次函数的表达式；
（2）若二次函数的图象都在直线
的上方，求m的取值范围.
19．（12分）运动队11月份安排4次体能测试，规定每位运动员一开始就要参加测试，一旦
某次测试合格就不必参加以后的测试，否则4次测试都要参加。若李明4次测试当次合
格的概率依次组成一公差为
的等差数列，且他直至第二次测试才合格的概率为
（1）求李明第一次参加测试就合格的概率P1（结果用分数表示）.
（2）求李明11月份体能测试能合格的概率.（结果用分数表示）
20．（12分）函数对任意的实数m，n有
，且当
时有
.
（1）求证在R上为增函数；
（2）若
解不等式
.
21．（14分）点
为抛物线
上横坐标为n的点，过点An作抛物线的切线
与x轴交于点Bn，设△OAnBn的面积为an（O为原点）.
（1）求an；
（2）设
，数列
的前n项之和为
，求证：
22．（12分）奇函数
的图象E过点
两点.
（1）求的表达式；
（2）求的单调区间；
（3）若方程
有三个不同的实根，求m的取值范围.
数学（文）参考答案
一、选择题（共60分，每小题5分）
1.D 2.B 3.A 4.B 5.C 6.B 7.D 8.B 9.A 10.C 11.A 12.C
二、填空题（共16分，每小题4分）
13．
14．
15．
16．
三、解答题（共74分）
17．（12分）解：
…………4分
又
………………7分
.
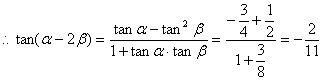……………………12分
18．（12分）解：（1）
为二次函数
……………………3分
又当
时，
令
得 
又AB=4 
………………7分
（2）由条件知
对于
恒成立
即
的取值范围是 
…………………………12分
19．（12分）解：（1）设四次测试合格的概率依次为
则
∴李明第一次参加测试就合格的概率为
………………6分
（2）设A为李明11月份体能测试合格的事件
则
…………………………9分
∴李明11月体能测试能合格的概率为
……………………12分
20．（12分）
（1）证明：设
则 
即
在R上为增函数…………………………5分
（2）解：
………………………7分
， 
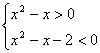………………9分
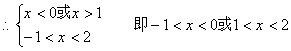
∴原不等式的解集为
………………12分
21．（14分）解：（1）由条件知
令
………………………………6分
（2）
……………………9分
………………………………………………12分
22．（12分）解：（1）
为奇函数
∴
∵图象过点
、
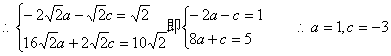
……………………………………………………5分
（2）
的增区间是
，减区间是（－1，1）…………10分
（3）
为使方程
有三个不等根，则
的取值范围是（－2，2）…………………………14分