甘肃省重点中学高三第二次阶段性联合考试
数 学
试 卷(理科)
2005 ![]() 10
10
一 ![]() 选择题:本大题共10小题,每小题5分,共50分
选择题:本大题共10小题,每小题5分,共50分
![]() 在每小题给出的四个选项中,只有一项是符合题目要求的
在每小题给出的四个选项中,只有一项是符合题目要求的
![]()
1.已知集合![]() 则AÇB等于
则AÇB等于
A .F B. ![]() C .
C .![]() D.
D. ![]()
2.设集合![]() ,若A∪B=R,则实数a的取值范围是 ( )
,若A∪B=R,则实数a的取值范围是 ( )
A.[-1,2] B.(-1,2) C.[-2,1] D.(-2,1)
3 ![]() 如果
如果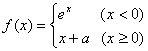 是连续函数,则
是连续函数,则![]() 等于( )
等于( )
A.1 B.-1 C.0 D.2
4 ![]() 函数
函数![]() ,在
,在![]() 处:
( )
处:
( )
A.无定义 B.极限不存在 C.不连续 D.不可导
5 ![]() 设
设![]() 是可导函数,且
是可导函数,且![]() ( )
( )
A.![]() B.-1 C.0 D.-2
B.-1 C.0 D.-2
6 ![]()
![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7 ![]() 已知随机变量ξ服从二项分布,且Eξ=2
已知随机变量ξ服从二项分布,且Eξ=2 ![]() 4,Dξ=1
4,Dξ=1 ![]() 44,则二项分布的参数n ,p的值为: ( )
44,则二项分布的参数n ,p的值为: ( )
A.n=4,p=0 ![]() 6
B.n=6,p=0
6
B.n=6,p=0 ![]() 4
4
C.n=8,p=0 ![]() 3
D.n=24,p=0
3
D.n=24,p=0 ![]() 1
1
8.有一道数学难题,学生A解出的概率为![]() ,学生B解出的概率为
,学生B解出的概率为![]() ,学生C解出的概率为
,学生C解出的概率为![]() ,若A
,若A ![]() B
B ![]() C三学生独立去解答此题,则恰有1人解出的概率为 ( )
C三学生独立去解答此题,则恰有1人解出的概率为 ( )
A.1 B.![]() C.
C.![]() D.
D.![]()
9 ![]() 5人站成一排,甲
5人站成一排,甲
![]() 乙两人之间恰有1人的不同站法的种数
( )
乙两人之间恰有1人的不同站法的种数
( )
A. 18 B.24 C. 36 D. 48
10 ![]() 设函数f(x)在定义域内可导,y= f(x)的图象如右图所示,
设函数f(x)在定义域内可导,y= f(x)的图象如右图所示,
则导函数y= f′(x)的图象可能为 ( )
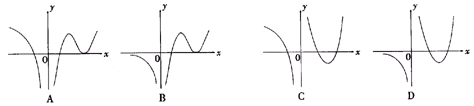
二 ![]() 填空题:本大题共4小题,每小题4分,共16分
填空题:本大题共4小题,每小题4分,共16分
![]() 把答案填在答题卡的相应位置
把答案填在答题卡的相应位置
![]()
11 ![]() 某工厂生产A
某工厂生产A ![]() B
B ![]() C三种不同型号的产品,产品数量之比依次为2:3:5
C三种不同型号的产品,产品数量之比依次为2:3:5 ![]() 现用分层抽样方法抽出一个容量为
现用分层抽样方法抽出一个容量为![]() 的样本,样本中A种型号产品有16件
的样本,样本中A种型号产品有16件 ![]() 那么此样本的容量
那么此样本的容量![]()
12 ![]()
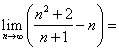 _________
_________ ![]()
|
则a-b=
![]()
14 ![]() 设函数
设函数![]() ,则
,则![]() ′
′![]() =____________________
=____________________
三 ![]() 解答题:本大题共6小题,每小题14分,共84分
解答题:本大题共6小题,每小题14分,共84分
![]() 解答应写出文字说明,证明过程或演算步骤
解答应写出文字说明,证明过程或演算步骤
![]()
15 ![]() 从4名男生和2名女生中任选3人参加演讲比赛
从4名男生和2名女生中任选3人参加演讲比赛
![]() 设随机变量
设随机变量![]() 表示所选3人中女生的人数
表示所选3人中女生的人数 ![]()
(I)
求![]() 的分布列;
的分布列;
(II)
求![]() 的数学期望;
的数学期望;
(III)
求“所选3人中女生人数![]() ”的概率
”的概率 ![]()
16 ![]() 已知函数
已知函数![]()
![]()
(I)求函数![]() 的单调区间;
的单调区间;
(II)求函数![]() 在区间[–3,2]上的最值
在区间[–3,2]上的最值 ![]()
17 ![]() 已知直线
已知直线![]() 为曲线
为曲线![]() 在点
在点![]() 处的切线,
处的切线,![]() 为该曲线的另一条切线,
为该曲线的另一条切线,
且![]()
![]()
(Ⅰ)求直线![]() 的方程;
的方程;
(Ⅱ)求由直线![]()
![]()
![]() 和
和![]() 轴所围成的三角形的面积
轴所围成的三角形的面积 ![]()
 18
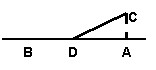
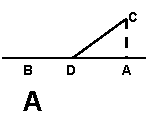
18 ![]() :如图,铁路线上AB段长100km,工厂C到铁路的距离CA=20km
:如图,铁路线上AB段长100km,工厂C到铁路的距离CA=20km ![]() 现在要
在AB段上某一处D,向C修一条公路,已知铁路与公路原料每吨每千米的运费分别为3元和5元
现在要
在AB段上某一处D,向C修一条公路,已知铁路与公路原料每吨每千米的运费分别为3元和5元
![]() 为了使原料从供应站B运到工厂C的运费最省,D应修在何处?
为了使原料从供应站B运到工厂C的运费最省,D应修在何处?
19 ![]() 设函数f(x)=x(x-1)(x-a),(a>1)
设函数f(x)=x(x-1)(x-a),(a>1)
(Ⅰ)求导数f¢ (x); 并证明f(x)有两个不同的极值点x1,x2;
(Ⅱ)若不等式f(x1)+ f(x2)£0成立,求a的取值范围 ![]()
20 ![]() 已知数列
已知数列![]() 是等差数列
是等差数列![]()
①求数列![]() 的通项
的通项![]() ;
;
②设数列![]() 的通项
的通项![]() ,记Sn是数列
,记Sn是数列![]() 的前n项和
的前n项和 ![]()
证明: ![]() (其中a>1)
(其中a>1)
参考答案
一 ![]() 选择题:本大题共10小题,每小题5分,共50分
选择题:本大题共10小题,每小题5分,共50分 ![]()
1~5 DD A D B 6~10 A B CC D
二 ![]() 填空题:本大题共4小题,每小题4分,共16分
填空题:本大题共4小题,每小题4分,共16分 ![]()
11 ![]() 80 12
80 12 ![]() –1 13
–1 13 ![]() 0 14
0 14 ![]() –15
–15
三 ![]() 解答题:本大题共6小题,每小题14分,共84分
解答题:本大题共6小题,每小题14分,共84分 ![]()
15 ![]() (I)解:
(I)解:![]() 可能取的值为
可能取的值为![]()
![]()
![]()
所以,![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 |
| P |
|
|
|
----------------------------------8分
(II)解:由(I),![]() 的数学期望为
的数学期望为
![]() ---------------------------------11分
---------------------------------11分
(II)解:由(I),“所选3人中女生人数![]() ”的概率为
”的概率为
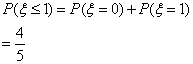 ----------------------------------14分
----------------------------------14分
16 ![]() (I)解:
(I)解:![]()
令 ![]() 得
得![]() ---------------------------------------4分
---------------------------------------4分
若 ![]() 则
则![]() ,故
,故
![]() 在
在![]() 上是增函数,
上是增函数,
![]() 在
在![]() 上是增函数
上是增函数 ![]() ------------------------------------7分
------------------------------------7分
若 ![]() 则
则![]() ,故
,故
![]() 在
在![]() 上是减函数
上是减函数 ![]() -----------------------------------------10分
-----------------------------------------10分
(II) ![]() ------------------------12分
------------------------12分
![]()
![]() -----------------14分
-----------------14分
![]()
17 ![]() (I) 解:
设直线
(I) 解:
设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
![]() ,由题意得
,由题意得![]() ,得直线
,得直线![]() 的方程为
的方程为![]()
![]()
![]()
![]() ,
,![]()
![]() 与该曲线的切点坐标为
与该曲线的切点坐标为![]() 由直线方程的点斜式,
由直线方程的点斜式,
得直线![]() 的方程为
的方程为![]()
![]() ------------------------8分
------------------------8分
(Ⅱ)由直线![]() 的方程为
的方程为![]() ,令
,令![]()
由直线![]() 的方程为
的方程为![]() ,令
,令![]()
由![]() 得
得![]() ------------------------12分
------------------------12分
设由直线![]()
![]()
![]() 和
和![]() 轴所围成的三角形的面积为S,则
轴所围成的三角形的面积为S,则
![]() -----------------------14分
-----------------------14分
18 ![]() 解:设DA=xkm,那么DB=(100-x)km,
解:设DA=xkm,那么DB=(100-x)km,
则CD=![]()
设每吨原料从供应站B运到工厂C的总运费为y,
![]() ,
,![]() ------------------------6分
------------------------6分
![]() ------------------------12分
------------------------12分
所以,当x=15(km),即D点选在距A点15千米时,总运费最省
![]() ------------------------14分
------------------------14分
19 ![]() I)
I)![]() ……(2分)
……(2分)

……(6分)
因此![]() 是极大值点,
是极大值点,![]() 是极小值点
是极小值点 ![]() ……(8分)
……(8分)
(II)因![]()
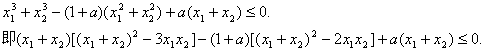
……(10分)
又由(I)知
![]()
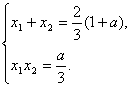
……(12分)
代入前面不等式,两边除以(1+a),并化简得
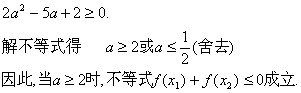
……(14分)
20 ![]() (I)设数列
(I)设数列![]() 的公差为d,由题意得
的公差为d,由题意得
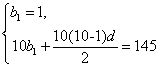
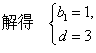
![]() -----------4分
-----------4分
(Ⅱ)![]()
![]() ;
;
![]()
![]()
要证明![]() , (其中a>1)
, (其中a>1)
只需证明![]() ----------------------6分
----------------------6分
下面用数学归纳法来证明(1)式成立 ![]()
(I)![]() , 所以(1)式成立
, 所以(1)式成立 ![]()
(II)假设当n=k(k≥1)时(1)式成立,即
![]()
当n=k+1时![]()
![]()
所以(1)式当n=k+1时成立 ![]()
由(I)(II)可知(1)式对任何正整数n都成立 ![]() -
--------------------12分
-
--------------------12分
又因为a>1所以Sn>![]()
![]() ---------------------14分
---------------------14分