05－06阜阳十中高三第二次月考数学试题
姓名：
号码 分数 
一、选择题：（每小题5分，共计60分）
1．已知函数
的图象过点
，则
的反函数的图象一定过点（ ）
．
．
．
．
2．设集合
，
，映射
满足
，则映射的个数为
（ ）
．1
．2
．3
．4
3．（文）已知－7，
，
，－1四个实数成等差数列，－4，
，
，
，－1五个实数成等比数列，则
=（ ）
A．1 B．－
（理）
（ ）
A．
B．
C．
D．
4．若
，则函数
的解集是
（ ）
．
．
．
．
5．已知数列
等于（ ）
A．445 B．
6．在
这四个函数中，当
时，使
恒成立的函数的个数是（ ）
A．0 B．
7．不等式组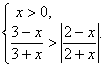
的解集是（ ）
A
B 
C
D 
8．数列
……的前n项和为 （ ）
（A）1－
（B）2－
（C）n(1－) （D）2－
＋
9．（文）等比数列{
}中，若各项均为正，且公比q≠1，则 （ ）
（A）＋
>
＋
（B）＋<＋
（C）＋＝＋ （D）＋与＋的大小关系不确定
（理）无穷等比数列{}的公比为q，q<1，首项＝1，若其每一项都等于它后面所有项的和的k倍，则k的取值范围是
（ ）
（A）[0, ＋∞) （B）(－∞, －2)
（C）(－∞, －2)∪(0, ＋∞) （D）(－2, 0)
10．（文）等比数列{}的前n项和是
，若
＝13
, ＋＝140， 
的值是（ ）
（A）90 （B）70 （C）50 （D）40
（理）若数列
满足＝5, 
＝
(n∈N)，则其前10项和是（
）
（A）200 （B）150 （C）100 （D）50
11．由奇数组成数组(3, 5), (7, 9, 11), (13, 15, 17, 19),……，第n组的第一个数应是 （ ）
（A）n(n－1) （B）n(n＋1) （C）n(n＋1)＋1 （D）n(n-1)＋1
12．数列{}的前n项和是，如果＝3＋2 (n∈N)，则这个数列一定是（ ）
（A）等比数列 （B）等差数列
（C）除去第一项后是等比数列 （D）除去第一项后是等差数列
二、填空题（每小题4分，共计16分）
13．若两个等差数列的前n项和之比为
，则这两个数列的第9项之比是
14．已知函数
的反函数为____
______
15．已知f (x)＝
，数列{an}满足
＝f (
) (n≥2)，且＝1，则＝
16．当
成等差数列时，有
成等差数列时，有
成等差数列时，有
，
由此归纳：当
成等差数列时有
如果
成等比数列，类比上述方法归纳出的等式为
答 题 卡 姓名
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
13 14 15 16
三、 解答题：
17．（本小题满分12分）在等比数列{an}的前n项中，a1最小，且a1+an=66，a2an-1=128，前n项和Sn=126,求n和公比q
18．（本小题满分12分）已知函数
和
的图象关于原点对称，且
（1）求函数的表达式；（2）解不等式
19．（本小题满分12分）（文）已知函数
在
处取得极值；
（1）求常数
的值;
（2）过点A（0，-32）作曲线
的切线，求此切线方程
（理）已知
在区间[-1，1]上是增函数
（1）求实数a的值所组成的集合A
（2）设关于x的方程
的两根为x1、x2，试问：是否存在实数m，使不等式
+tm+1
≥x1-x2对任意a∈A及t∈[-1,1]恒成立？若存在，求出m的取值范围；若不存在，说明理由
20．（本小题满分12分）
已知数列
满足
（Ⅰ）求证：数列
为等差数列；
（Ⅱ）试问
是否是数列中的项？如果是，是第几项；如果不是，请说明理由
21、（本小题满分12分）数列
（1）若数列
（2）求数列
的通项公式
（3）求
的前n项和
22． （本小题满分14分）（文）已知数列{}为等差数列，公差d≠0，{}中的部分项组成的数列
,
,
,……,
,……恰为等比数列，其中
＝1, 
＝5,
＝17,
(1)
求与d的关系 (2)求
＝f (n)的解析式；
(3)
求＋＋＋……＋
(理)设数列
的各项都是正数, 且对任意
都有
记
为数列的前n项和
(1) 求证: 
(2)
求数列的通项公式
(3) 若
(
为非零常数, ), 问是否存在整数, 使得对任意
, 都有
05－06阜阳十中高三第一次月考数学试题参考答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | BC | B | B | B | C | B | AC | DD | C | A |
13 
14
15
16 
17．∵{an}为等比数列 ∴a1·an=a2·an-1 ∴a1·an=128 a1+an=66 a1=2 an=64……6分
 |
∵
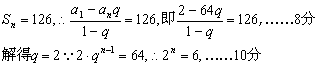解得n=6,∴n=6,q=2 ……12分
18．解：(1) 
……4分
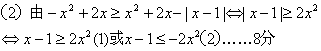
解（1）得
；解（2）得
所以原不等式的解集为
……12分
19、解：（1）
，又
在处取得极值，所以
即
解得
……4分
(2)由（1）得
，
不在曲线上，
设过点A的切线切曲线于点P（
），
切线方程为：
……8分
因为点A在切线上，所以
解得
切线方程为：
……12分
解：（1）∵f(x)在[-1,1]上是增函数
∴f’(x)≥0对x∈[-1,1]恒成立
 |
设φ(x)=x2-ax-2，则有
∵对x∈[-1,1],f(x)是连续函数，且只有当a=1时，f’(-1)=0，
以及当a= -1时，f’(1)=0,∴A={a-1≤a≤1}……4分
（2）由
 |
∴
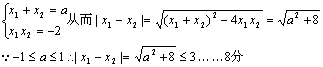要使不等式m2+tm+1≥x1-x2对任意a∈A及t∈[-1,1]恒成立，当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立 设g(t)=m2+tm-2=mt+m2-2
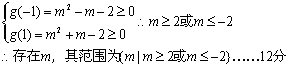
则有
20、解：（Ⅰ）当
…………2分
两边同除以
，…………4分
即
成立，
∴
为首项，d=4为公差的等差数列 …………6分
（Ⅱ）由（Ⅰ）得，
……8分
∴
…………9分
设是数列的第t项，则
解得，t=11∈N*，………11分
∴是数列的第11项 …………12分
21、解：（1）由
∴
……4分
（2）
……8分
(3) 略……12分
22（文）(1) 依题意，, , 
成等比数列，有
＝,
∴ (＋4d)2＝ (＋16d), ∴ ＝2d, ……4分
又
＝3, ∴ q＝3, ……6分
∴ 
＝
·
－1＝－1, 又＝＋(－1)d, ……8分
∴－1＝ ＋(－1)d, ＝2d, d≠0, ∴＝2·
－2 ……12分
(2) ＋＋＋……＋＝
……14分
(理) 证明：(1)在已知式中,
当
时, 
∵
∴
………(1分)
当
时, 
①
②
由①－②得, 
………(3分)
∵
∴
即
∴适合上式,
………(5分)
(2)由(1)知, 
③
当时, 
④
由③－④得,
……(8分)
∵
, ∴
, 数列是等差数列,首项为1,
公差为1, 可得
………(10分)
(3) ∵, ∴
………(11分)
∴
,
∴
⑤………(12分)
当
时, ⑤式即为
⑥
依题意, ⑥式对
都成立, 当
时,
⑤式即为
⑦依题意, ⑦式对都成立,
∴
………(13分) ∴
又
,
∴存在整数
, 使得对任意
, 都有 ………(14分)