福州八中学年度高三年级第二次质量检查
数学（理）
YCY
考试时间：120分钟 试卷满分：150分
一 
选择题：本小题共12小题，每小题5分，共60分，在每小题给出年四个选项中，只有一项，只有一项是符合题目要求的
1．函数
的导数为 （ ）
A．
B．
C．
D．
2．如果随机变量ζ服从正态分布N（1，0 52），则对3ζ来说，有 （ ）
A．E（3ζ）=3，D（3ζ）=0 5 B．E(3ζ)=1，D(3ζ)=
C．E(3ζ)=3，D（3ζ）=1 5 D．E(3ζ)=3，D(3ζ)=2 25
3．函数
的单调减区间为 （ ）
A．
B．
C．[－1，1] D．
4．抛掷两颗骰子，所得点数之和记为ζ，则ζ=4表示的随机试验的结果是 （ ）
A．两个都是4点 B．一个是1点，另一个是3点
C．两个都是2点 D．一个是1点，另一个是3点；或两个都是2点
5．曲线
在点P（－1，3）处的切线方程是 （ ）
A．
B．
C．
D．
6．
（ ）
A．
B．
C．
D．
7．若
，其中a b∈R，i是虚数单位，则
= （ ）
A．0 B．2 C．5 D．10
8．有一笔统计资料，共有5个数据如下（不完全以大小排列）：4，5，7，6，x，已知这组
数据的平均数为6，则这组数据的方差为 （ ）
A．4 B．2 C．
D．2 5
9．函数
，已知
在
时取得极值，则
= （ ）
A．2 B．3 C．4 D．5
10．从数字1，2，3，4，5，中随机抽取3个数字（允许重复）组成一个三位数，其各位数字之和等于9的概率为 （ ）
A．
B．
C．
D．
11．设函数y=的图象如右图所示，则导函数
y=
的图像可能为（ ）
12．有限数列A=（
，…，
），Sn为其前n项和，定义
为A的“凯森和”；如有2004项的数列（，…，
）的“凯森和”为2005，则有2005项的数列（1，，…，）的“凯森和”为 （ ）
A．2004 B．2005 C．2006 D．2008
二 填空题：本大题共4小题，每小题4分，共16分，请把答案填在答题纸的空格中
13．若
则
14．设随机变量
服从二项分布B（6，），则P（=3）=
15．用数学归纳法证明等式1+2+3+…+（2n+1）=（n+1）（2n+1）时，当n=1左边所得的项是1+2+3；从“k→k+1”需增添的项是
16．设l为平面上过点（0，1）的直线，l的斜率等可能地取
，
用表示坐标原点到l的距离，则随机变量的数学期望E=
三 解答题：本大题共6小题，共74分，解答过程应写出文字说明 证明过程或演算步骤
17．（本大题满分12分）
高三数学暑期办有竞赛班和提高班，一次考试中，两班的成绩如下：
竞赛班：
|
| 110 | 115 | 125 | 130 | 140 |
| P | 0 | 0 | 0 | 0 | 0 |
提高班：
|
| 100 | 115 | 125 | 130 | 145 |
| P | 0 | 0 | 0 | 0 | 0 |
其中A B分别表示竞赛班 提高班的成绩 试问哪一班的学习成绩较好？
18．（本大题满分12分）
已知数列{an}的通项公式是
，记
（1）写出数列{bn}的前三项；
（2）猜想数列{bn}通项公式，并用数学归纳法加以证明；
（3）令
，求
的值
19．（本大题满分10分）
已知函数
，当且仅当
，
时取得极值，且极大值比极小值大4，求a b的值
20．（本大题满分12分）
某县农民年均收入服从μ=500元，σ=30元的正态分布
（1）求此县农民年收入在500元~530元间人数的百分比；
（2）如果要使农民的年均收入在（μ－a，μ+a）内的概率不小于0 95，则a至少为多大？
（Φ（0）=0 5000 Φ（0 05）=0 5199 Φ（1）=0 8413 Φ（1 96）=0 9750
Φ（2）=0 9772）
21．（本大题满分14分）
在
上为增函数，在[0，2]上减函数，又方程
三个根为α，2，β
（1）求c；
（2）比较
与2的大小的大小；
（3）求α－β的范围
22．（本大题满分14分）
已知二次函数
的图象的顶点坐标是（
，且
（1）求
的表达式，并求出 
的值；
（2）数列{an} {bn}，若对任意的实数
都满足
，
其中
是定义在实数R上的一个函数，求数{an} {bn}的一个通项公式；
（3）设圆Cn：
，若圆Cn与圆Cn+1外切，{
}是各项都是正
数的等比数列，记Sn是前n个圆的面积之和，求
福州八中2005—2006学年度高三年级第二次质量检查
数学（理）试题参考答案
YCY
一 选择题
1．B 2．D 3．A 4．D 5．C 6．A 7．D 8．B 9．D 10．C 11．D 12．B
二 填空题
13．4 14．
15．（2k+2）+（2k+3） 16．
三 解答题：（共80分）
17．解：
=110×0 1+115×0 2+125×0 4+130×0 1+140×0 2=125
=100×0 1+115×0 2+125×0 4+130×0 1+145×0 2=125
两个班的平均成绩都是125，此时我们再看它们与平均成绩的偏离程度，即它们的方差大小
0 1×(110－125)2+0
2×(115－125)2+0
4×(125－125)2+0
1×(130－125)2+0
2×(140－125)2=90
0 1×(110－125)2+0 2×(115－125)2+0
4×(125－125)2+0
1×(130－125)2+0
2×(140－125)2+0
2×(145－125)2=165
∴提高班的成绩与其平均值偏差很大，即取值较分散，所以尽管它们中有的成绩较高，但不合格的人数也较多，故认为竞赛班比提高班的成绩质量要好
18．（1）
；（2）
，
（3）
19．解：
因为当且仅当
时取得极值，所以，一方面，
即 
另一方面，由于
，所以，
所以，必有取得极大值，在取得极小值，所以，
，即
与
联立，解得：
20．解：设表示此县农民的年均收入，则～N（500，302）
（1）P（500<<530）=
即此县农民年均收入在500元－530元间的人数约为34 31%
（2）
则：
查表得：
∴要使农民的年均收入在（500－a，500+a）内的概率小于0 95，a不能小于3 92
21．（1）
为增函数，（0，2）为减函数
………………………………………………4分
（2）
两根
……………………9分
（3）
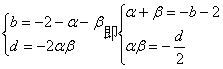
……………………………………………………………………14分
22．（1）由已知得
………………4分
（2）
即
=1 ①
即
=2n+1 ①
由①②得
…………………………………………8分
（3）
设数列
的公比为q，则
……………10分 即
，
…………………………12分
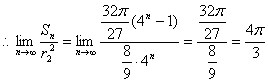……………………………………14分