第一讲 集合
知识点及方法 集合的概念;集合的运算;子集的个数;集合中元素的个数;集合间的关系;集合与充要条件;方程、不等式中与集合有关的问题;补集的思想.
1. 子集的个数
(1)
若
,求满足这个关系式的集合A的个数
(2)
已知
①求集合
的子集个数 ②求满足条件
的集合
的个数
2. 集合中元素的个数
(1) 已知集合M,N分别含有8个、13个元素,若
中有6个元素, ①求
中的元素个数. ②当 含多少个元素时,
.
(2) 对某城市1000户的居民生活水平进行调查，统计结果有彩电的有682户，有电冰箱的有819户， 彩电和电冰箱二者都有的535户，问彩电和电冰箱至少有一种的有多少户。
(3) 某文艺小组共有10名成员,每人至少会唱歌和跳舞中的一项,其中7人会唱歌跳舞5人会,现从中选出会唱歌和会跳舞的各一人，表演一个唱歌和一个跳舞节目,问有多少种不同的选法？
(4) 某运动队有10名赛艇运动员,其中7人会划左桨,6人会划右桨，要选出6名运动员参加比赛，其中3名左桨选手，3名右桨选手,问有多少种不同的组队方案？
(5) 某班一天排7节不同的课，要求体育课不排第一节，语文课不排第七节，问有多少种不同的排法？（只列式，不计算）
3. 集合间的关系
判断下列两集合之间的关系
⑴
(2)
(3)
(4)
(5)
(6)
4. 集合与充要条件
判断充要条件关系
(1) x>0 是 x2>0
(2) x2=1 是 x=1
(3) lgf(x)>lgg(x) 是 f(x)>g(x)
(4) 0<x<5 是 ∣x-2∣<3
(5) 
是 
,
(6) 
是 
(7) 
是
(8) 
是 
(9) 
是
(10) 
是 
(11) 
是
4. 方程、不等式与集合
(1) 已知方程
的解集分别为
写出方程
的解集
写出方程
的解集
写出方程
的解集
(2) 已知不等式
的解集分别为
的解集分别为
写出不等式
的解集.
(3)
设全集为R,记
,试写出
的解集.
(4)
已知
求p的取值范围
(5)
设集合
若
,求a的取值范围.
(6)
已知集合
,且
求p的取值范围.
(7)
已知集合
且求a的取值范围.
(8)
已知集合
且
求A的取值范围.
(9)
已知集合
且,求a的取值范围.
(10) 已知 
,且
求m的取值范围.
(11) 已知集合
且
求p的取值范围.
(12) 设
若求m的取值范围.
(13) 已知函数
集合
且
求a的取值范围.
(14) 已知
若
求a的值.
(15) 已知
①若
求a的取值范围.②若
且
求b,c的值.
(16) 集合
,若
求a的取值范围.
(17) 
求实数m的取值范围.
(18) 已知集合
且
求m的取值范围.
5. 用补集思想解题
(1)
已知函数
的图象与x轴的交点至少有一个在原点左侧，求实数m的取值范围.
(2) 从5本中文书和6本英文书中任取3本,其中至少有一本英文书的取法种数是多少？
(3) 从8名男生和4名女生中选出5名学生参加数学竞赛,至少有两名女生的取法种数是多少？
第二讲 函数的定义域
知识点及方法求函数的定义域;定义域在函数、方程、不等式中的应用
1.求函数的定义域
(1)
(2) 
(3) 
(4) 设函数
的定义域是[0,1],求
的定义域.
(5) 设函数的定义域是[0,2],
求
的定义域.
(6) 设函数的定义域是
求函数
的定义域.
(7) 设函数的定义域是[
],
求函数
的定义域.
(8) 设函数的定义域是 
, 求函数
的定义域.
(9) 设函数
的定义域是[0,1],
求函数
的定义域.
2. 定义域的“隐藏”性
2.1换元法引起的变量范围即函数定义域的变化
(1) 求函数
的值域.
(2) 求函数
的值域.
(3) 求函数
的值域
(4) 若方程
有解,求实数
的取值范围.
(5) 若方程
有负根,求实数的取值范围.
(6) 若方程
的两根都大于2,求
的取值范围.
(7) 若方程
的所有解都大于1,求的取值范围.
2.2 在求条件值域、最值中,注意条件关系式中变量的范围
(1) 已知
求
的取值范围.
(2) 已知
,求
的取值范围.
(3) 已知
,求
的取值范围.
(4) 
是方程
的两个实根，求
的取值范围.
2.3 方程、不等式的同解原理本质上是保持方程和不等式中的函数的定义域在变形中不变
(1) 解不等式 
(2)
比较大小: 
与
(3)
求函数f(x)=
的最值.
(4)
求函数
的值域.
(5)
考察函数
的奇偶性.
第三讲 函数的值域和最值
知识点及方法 二次函数法；函数单调性法；反解法（反函数法）；数形结合法；均值不等式法
1. 二次函数法（用换元法化为二次函数）
求下列函数的值域
(1)
(2)
(3)
(4)
(5)
)
(6)
(7)
(8)
(9)
(10) 已知函数的值域是
,求函数
的值域.
(11) 
,
(12) 
(13) 若
求函数
的取值范围.
(14) 若
求函数
的值域.
2. 含参的二次函数的值域、最值
(1) 求a, 使函数y=2x2+5ax+2a的图象的顶点最高.
(2) m为何值时, 二次函数y=x(2m-3x)+4m的顶点位置最低？
(3) 设y=x2+px+q的最小值为0, 求q.
(4) 已知y=x2+2x+a,x∈[-3,2]最大值为4, 求a的值.
(5) 已知y=x2+2ax+1,x∈[-1,2]最大值为4, 求a的值.
(6) 已知y=ax2+2ax+1,x∈[-3,2]最大值为4, 求a的值.
(7) 巳知y=4mx2-2x+1,
最小值为7, 求m的值.
(8) 设y=x(2a-x),x∈[0,2]最大值为a2,求的取值范围.
(9) 求函数y=2msinx-cos2x的最大值.
(10)若函数y=asin2x+2cosx-a-2(a∈R)的最小值为m, 求m的表达式.
(11)当函数y=sin2x+acosx+
(0≤x≤
)取最大值1, 求a.
(12)设关于x的函数y=2cos2x-2acosx-(2a+1)的最小值为f(a). ①用a写出的f(a)表达式. ②试确定能使f(a)=
的a, 并对这个a, 求y的最小值.
(13)已知函数y=x2-2x,x∈[t,t+1],求函数在[t,t+1]上取最小值.
(14)设y=-x2-4x+1,x∈[t-1,t+1], 试写出函数在[t-1,t+1]上的最大值.
(15)设函数
的最大值为3，求a的值.
(16)
设A为曲线
上任意一点, B（0, b）（b≥0）为y轴上一点, 求｜AB｜的最小值。
(17) 在长、宽分别是a（a＞1）, 1的矩形中, 截得平行四边形ABCD，
求平行四边形ABCD面积的最大值。
(18) 已知a,b∈R+,a≠b,
,
求m.
(19) 0<a<1,x,y满足
如果
,求a.
(20) 求函数
的最小值.
(21) 已知函数
在区间[－1，1]上的最大值是14，求 .
(22) 已知椭圆
,B是短轴上一个端点, P是椭圆上一动点, 求｜PB｜最大值.
(23) 已知点P（a,0）（a∈R）,M是双曲线
上的动点, 求｜PM｜的最小值.
(24) 已知点P是抛物线y2=4px(p>0)上动点，Q（1, 0）, 求｜PQ｜的最小值.
3. 函数单调性法
求下列函数的值域
(1)
(2)
(3)
(4)
已知二次函数
的定义域和值域都为
,求b的值.
(5)
(6)
(7)
(8)
(9)
(10) 函数
在区间
上的最大值与最小值之差为1，求a的值.
4.反解法（反函数法）
求下列函数的值域
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
5. 数形结合法
求下列函数的值域
(1)
(2)
(3)
(4)
(5)
(6)
已知
求
的最大值和最小值.
(7)
对于任意实数
,设函数是
与中较小者,求的最大值.
方法的综合
求函数
的最大值.
6. 已知函数的值域求参数的值
(1) 已知函数
的值域是
,求的值.
(2) 已知函数
的值域是
求的值.
7. 函数的值域与均值不等式
7.1 求下列函数的值域或最值
(1)
.
(2) 若下面各式中字母均为正数
① 求
的最大值. ② 求x +
的最小值. ③ 当log4x+log4y=2时, 求
的最小值.
(3)
(4)
(5)
点
在直线
上, 求
的最小值.
7.2 在解析几何中的应用
(1)
过点
作直线
与
轴正方向交于两点,
①当△
面积最小时，求直线的方程．
②当在两轴上截距之和最小时，求直线的方程．
③当
最小时,求直线的方程．
(2)
在直线
上求一点
使点
对
的张角最大.
(3)
已知
的图象中，有一长为定值的线段
的端点分别在两条射线上移动.
①求的中点的轨迹方程.
②设方程为
,求
的关系.
③当
时，求
的取值范围.
(4)
定长为的线段两端点在抛物线
上移动.求动点的中点的轨迹方程.
求离
轴最近的中点
的坐标.
7.3 若干应用题
(1) 某罐装饮料厂为降低成本要将制罐材料减少到最小，假设罐装饮料筒为圆柱体（视上、下底为平面），上下底半径为r，高为h，若体积为V，上下底厚度分别是侧面厚度的2倍，试问当r与h之比是多少时用料最少？
(2)
商店经销某种商品，年销售量为D件，每件商品库存费用为I元，每批进货量为Q件，每次进货所需费用为S元，现假设商店卖完该货物时立即进货，使库存量为平均
件，问每批进货件数Q为多大时，整个费用最省？
(3) 某轮船公司争取到一个相距1000海里的甲、乙两地的客运航线权．已知轮船限载人数为400人，轮船每小时使用的燃料费用和轮船速度的立方成正比例，轮船的最大时速是25海里/时，当船速为10海里/时，它的燃料费用是每小时30元，其余费用（不论速度如何）都是每小时480元．你能为该公司设计一种较为合理的船票价格吗？
(4) 为了确保交通安全，交通部门规定：某事故易发地段内的车距d正比于车速v（千米/时）的平方与车身长（米）的积，且最小车距不得少于半个车身长．假定车身长均为s（米），且车速为50（千米/时）时，车距恰为车身长S．问交通繁忙时，应规定怎样的车速，才能使此地段车流量Q最大？
(5)
铁道车运行1小时所需的成本由两部分组成，固定部分m元，变动部分与运行速度
（千米/时）的平方成正比例，比例系数为 k（k＞0），如果机车匀速从甲站开往乙站，为使成本最省，应以怎样的速度运行？
(6) 某罐装饮料厂为降低成本要将制罐材料减少到最小，假设罐装饮料筒为正圆柱体（视上、下底为平面），上、下底半径为r，高为h．若体积为V，上、下底厚度分别是侧面厚度的2倍，试问当r与h之比是多少时用料最少？
(7) 商店经销某种货物，年销售量是5万件．因集装运输要求，这批货物可分为若干次等量进货，每次运费500元．商店进货后，需人库暂存，销售完后可立即进货．仓库年租金按最大储存量时每件4元收费（以后不超量的各次货物进出不再收费），为尽量减少运费和库存费总开支，每次进货应是多少件？全年运费和库存费总开支最少多少元？
(8) 在半径为R的球内挖去一个以球的直径为轴的圆柱型孔．当孔的面积（即圆柱的侧面积）最大时，球套在杆上不易打滑，此时的孔半径为多少？
(9) 要建造一个底面为正方形，容量为32m3的柱形露天水池．(A)问水池尺寸如何选取，才能使所用材料最省？(B) 若池底材料成本30元／m2，池壁材料成本为20元/m2，问选取怎样的尺寸，水池造价最低？
(10) 已知圆柱的表面积为S , 求圆柱体积V的最大值.
(11)
已知一个长方体的长、宽、高之和等于
，求它的体积的最大值.
(12) 圆锥底面半径为R，高为H，求它内接圆柱的最大体积。
|
|
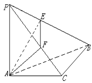
(13)
如图，已知直线角三角形ABC的斜边为AB，过A作AP
平面ABC，
AEPB交PB于E，AFPC交PC于F，① 求证：PB平面
AEF；② 设AP＝AB＝2，
是变量，求四面体PAEF体积的
最大值，并求出这时
的值.