天津市培英外语实验学校第二学期高三年级总复习质量调查(二)
数学试卷(理科)
第I卷(选择题 共50分)
一. 选择题:(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案的标号字母填在题后的括号内)
1. 过点(2,-2)且与双曲线![]() 有相同渐近线的双曲线方程是( )
有相同渐近线的双曲线方程是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
2. 函数![]() ,
,![]() 的最小正周期是( )
的最小正周期是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
3. 若m、n都是正整数,那么“m、n中至少有一个等于1”是“![]() ”的( )
”的( )
A. 充分而不必要的条件 B. 必要而不充分的条件
C. 充要条件 D. 既不充分也不必要的条件
4. 已知x、y满足约束条件: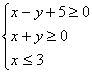 ,则
,则![]() 的最小值为( )
的最小值为( )
A. -3 B.
![]() C.
0 D.
C.
0 D.
![]()
5. 在空间,下列命题正确的是( )
A. 若三条直线两两相交,则这三条直线确定一个平面
B. 若直线m与平面![]() 内的一条直线平行,则m//
内的一条直线平行,则m//![]()
C. 若平面![]() ,则过
,则过![]() 内一点P与l垂直的直线垂直于平面
内一点P与l垂直的直线垂直于平面![]()
D. 若直线a//b,且直线![]() ,则
,则![]()
6. 函数![]() 的定义域是( )
的定义域是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
7. 已知![]() ,且
,且![]() 的值是( )
的值是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
8. 若随机变量![]() 的分布列为
的分布列为 其中
其中![]() ,则下列结果中正确的是( )
,则下列结果中正确的是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
9. 已知函数f(x)是定义在R上的奇函数,当x<0时,![]() ,如果
,如果![]() 是f(x)的反函数,则
是f(x)的反函数,则![]() 的值是( )
的值是( )
A. ![]() B.
2 C.
B.
2 C.
![]() D.
D.
![]()
10. 已知![]() ,
,![]() ,则a、b、c的大小关系是( )
,则a、b、c的大小关系是( )
A. c<b<a B. a<b<c
C. b<c<a D. b<a<c
第II卷(非选择题 共100分)
二. 填空题:(本大题共6小题,每小题4分,共24分,请把答案直接填在题中横线上)
11. 若![]() 在复平面内对应的点位于_________象限。
在复平面内对应的点位于_________象限。
12. 若椭圆经过点(2,3),且焦点为![]() ,则这个椭圆的离心率等于_________________。
,则这个椭圆的离心率等于_________________。
13. 一个正方体的全面积为![]() ,它的顶点全都在一个球面上,则这个球的表面积为______________。
,它的顶点全都在一个球面上,则这个球的表面积为______________。
14. 已知![]() 的夹角的余弦值等于_________________。
的夹角的余弦值等于_________________。
15. 6本不同的书分给4个学生,每人至少1本,共有_________种不同的分法。(用数字作答)
16. 定义一种运算“![]() ”为
”为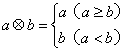 ,那么函数
,那么函数![]() 的值域为_________________。
的值域为_________________。
三. 解答题:(本大题共6小题,共76分,解答应写出文字说明,证明过程或演算步骤)
17. (本小题满分12分)
解关于x的不等式![]()
18. (本小题满分12分)
袋子内装有大小相同的15个小球,其中有n个红球,5个黄球,其余为白球。
(I)从中任意摸出2个小球,求得到2个都是黄球的概率;
(II)如果从中任意摸出2个小球,得到都是红球或都是黄球的概率为![]() ,求红球的个数;
,求红球的个数;
(III)根据(II)的结论,试计算从袋中任意摸出3个小球得到至少有1个白球的概率。
19. (本小题满分12分)
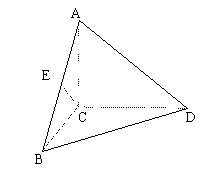
如图:已知在![]() 中,
中,![]() ,BC=CD=1,
,BC=CD=1,![]() 平面BCD,
平面BCD,![]() ,E是AB的中点。
,E是AB的中点。
(I)求直线BD和CE所成的角;
(II)求点C到平面ABD的距离;
(III)若F是线段AC上的一个动点,请确定点F的位置,使得平面![]() 平面DEF。
平面DEF。
20. (本小题满分12分)
已知a>0且![]() ,数列
,数列![]() 是首项为a,公比为a的等比数列,又
是首项为a,公比为a的等比数列,又![]()
![]() 。
。
(I)求数列![]() 的前n项和
的前n项和![]() ;
;
(II)若a=3,求![]() 。
。
21. (本小题满分14分)
已知函数![]()
(I)若函数![]() 在x=2时取得极植,求实数a;
在x=2时取得极植,求实数a;
(II)若![]() ,求
,求![]() 上的最大值。
上的最大值。
22. (本小题满分14分)
在以O为坐标原点的直角坐标系中,已知点T(-8,0),点M在y轴上,点N在x轴的正半轴上,且满足![]() 。
。
(I)当M在y轴上移动时,求点P的轨迹C;
(II)若动直线l经过点D(4,0),交曲线C于A、B两点,求是否存在垂直于x轴的直线![]() 被以AD为直径的圆截得的弦长恒为定值?若存在,求出
被以AD为直径的圆截得的弦长恒为定值?若存在,求出![]() 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
天津市培英外语实验学校第二学期高三年级总复习质量调查(二)
数学试卷(理科)参考答案及评分标准
一. 选择题:(每小题5分,共50分)
1. D 2. B 3. C 4. A 5. D 6. B 7. A 8. C 9. B 10. B
二. 填空题:(每小题4分,共24分)
11. 第四; 12. ![]() ; 13.
; 13.
![]() ; 14.
; 14. ![]() 15.
2640; 16.
15.
2640; 16. ![]()
三. 解答题:(共76分,以下各题为累计得分,其他解法请相应给分)
17. 解:①当a=0时,化为![]() …………2分
…………2分
解集为![]() …………4分
…………4分
②当a>0时原不等式等价于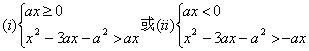 …6分
…6分
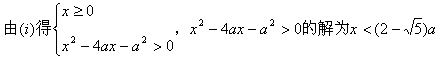
![]() …………8分
…………8分
![]()
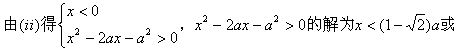
![]() …………11分
…………11分
![]()
![]() ,a>0时,解集为
,a>0时,解集为![]()
![]()
18. 解:(I)从15个小球中摸出2个小球都是黄球的概率为
![]()
(II)设有n个红球,由题意知![]()

(III)由(II)知有4个红球,故有6个白球,设摸出3个小球得到至少有1个白球为事件A
则无白球的概率为![]()
![]()
19. 解:(I)延长AC到G,使CG=AC,连结BG、DG,E是AB中点
![]()
故直线BG和BD所成的锐角(或直角)就是CE和BD所成的角……2分

(II)设C到平面ABD的距离为h
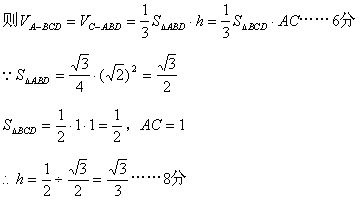

20. 解:(I)![]() …2分 故
…2分 故![]()
![]() …3分
…3分
于是![]() …
…![]() …
…![]() ,…4分
,…4分
![]() …
…![]() ,两式相减得
,两式相减得
![]() …
…![]() …6分
…6分![]() …8分
…8分
∴![]() …9分
…9分
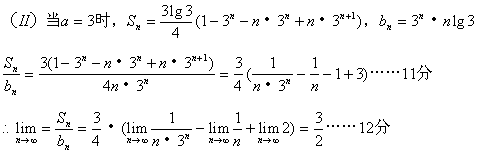
21. 解:(I)![]()

![]()
有

……9分


22. 解:(I)设点P(x,y),由![]() ,知P是M、N中点,又M在y轴上,N在x轴正半轴上
,知P是M、N中点,又M在y轴上,N在x轴正半轴上
故M坐标为(0,2y),N坐标为(2x,0)(x>0)……1分
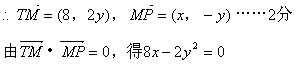
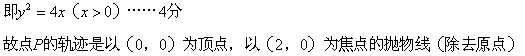
……5分
(II)设AD中点为H,垂直于x轴的直线l’的方程为![]()
以AD为直径的圆交l’于E、F两点
EF的中点为G……7分