襄樊市高三调研测试(2006.4)
数 学(文史类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页,第Ⅱ卷3至4页,共150分,考试时间120分钟。
注意事项:
1.请考生将自己的学校、班级、姓名、考号填写在答题卷内密封栏中,将考号最后两位填在答题卷右下方座位号内,同时请认真阅读答题卷上的注意事项。
2.第Ⅰ卷每小题选出正确答案后用2B铅笔把答题卡上对应题目的答案代号涂黑,如需改动,必须用橡皮擦干净后,再选涂其它答案。第Ⅱ卷用黑色签字笔直接答在答题卷每题对应的答题区域内,答在试题卷上无效。
3.考试结束后,监考人员将试题卷、答题卡和答题卷一并收回。
试题卷 第 Ⅰ 卷 (选择题,共50分)
一.选择题(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1. “两条直线没有公共点”是“这两条直线异面”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2. 函数![]() 的反函数为
的反函数为![]() ,若
,若![]() ,则x的取值范围是
,则x的取值范围是
A.(-∞,0) B.(-1,1) C.(1,+∞) D.(-∞,-1)
3. 若命题P:x∈A∩B,则命题非P是
A.x∈A∪B B.![]() A∪B C.x
A∪B C.x![]() A或x
A或x![]() B D.x
B D.x![]() A且x
A且x![]() B
B
4. 已知l、m为两条不重合的直线,α、β为两个不重合的平面,则下列条件中可以判断平面α与平面β平行的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5. 定义运算![]() ,则符合条件
,则符合条件![]() 的点P(x,y)的轨迹方程为
的点P(x,y)的轨迹方程为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6. Sn为等差数列{an}的前n项和,S9=-36,S13=-104,等比数列{bn}中, b5=a5,b7=a7,则b6等于
A.![]() B.
B.![]() C.
C.![]() D.无法确定
D.无法确定
7. 设点P是曲线:![]() 为实常数)上任意一点,P点处切线的倾斜角为
为实常数)上任意一点,P点处切线的倾斜角为![]() ,则
,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]()
C.[0,![]() )∪
)∪![]() D.[0,
D.[0,![]() )∪
)∪![]()
8. 已知定义在R上的偶函数f(x)的单调递减区间为[0,+∞![]() ,则不等式
,则不等式![]() 的解集是
的解集是
A.(1,2) B.(2,+∞) C.(1,+∞) D.(-∞,1)
9.
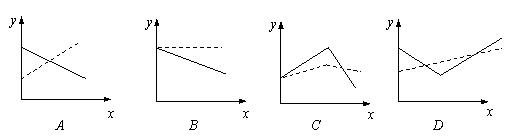 在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线
在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线![]() ,另一种是平均价格曲线
,另一种是平均价格曲线![]() (如f (2) = 3是指开始买卖后二个小时的即时价格为3元;g (2)
= 3表示二个小时内的平均价格为3元),下图给出的四个图像中,实线表示
(如f (2) = 3是指开始买卖后二个小时的即时价格为3元;g (2)
= 3表示二个小时内的平均价格为3元),下图给出的四个图像中,实线表示![]() ,虚线表示
,虚线表示![]() ,其中可能正确的是
,其中可能正确的是
10. 用0、1、2、3、4这五个数字组成无重复数字的五位数,其中恰有一个偶数字夹在两个奇数字之间的五位数的个数是
A.12 B.28 C.36 D.48
试题卷 第 Ⅱ 卷(非选择题,共100分)
二.填空题(本大题共5小题,每小题5分,共25分.将正确答案填在答题卷对应题号的横线上.)
11. ![]() 展开式中的常数项是 ▲ .
展开式中的常数项是 ▲ .
12. 将函数![]() 的图像按向量a平移后与
的图像按向量a平移后与![]() 的图像重合,则向量a= ▲ .
的图像重合,则向量a= ▲ .
13. 设抛物线![]() 的焦点为F,经过点P(2,1)的直线l与抛物线相交于A、B两点,且点P恰为AB的中点,则 AF + BF = ▲ .
的焦点为F,经过点P(2,1)的直线l与抛物线相交于A、B两点,且点P恰为AB的中点,则 AF + BF = ▲ .
14.  某地区有A、B、C三家养鸡场,鸡的数量分别为12 000只、8 000只、4 000只,为了预防禽流感,现用分层抽样的方法从中抽取一个容量为120只的样本检查疫情,则从A鸡场抽取的个数为 ▲ .
某地区有A、B、C三家养鸡场,鸡的数量分别为12 000只、8 000只、4 000只,为了预防禽流感,现用分层抽样的方法从中抽取一个容量为120只的样本检查疫情,则从A鸡场抽取的个数为 ▲ .
15. 一个表面积为![]() 的球放在如图所示的墙角处,正三角形木板ABC恰好将球盖住,则墙角O到木板的距离为 ▲ .
的球放在如图所示的墙角处,正三角形木板ABC恰好将球盖住,则墙角O到木板的距离为 ▲ .
三.解答题(本大题共6小题,满分75分。解答应写出文字说明、证明过程或演算步骤。)
16. (本大题满分12分)已知△ABC是锐角三角形,三个内角为A、B、C,已知向量p![]() ,q
,q![]() ,若p与q是共线向量,求函数
,若p与q是共线向量,求函数![]() 的最大值.
的最大值.
17. 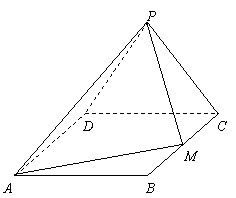 (本大题满分13分)如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC
(本大题满分13分)如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC![]() ,M为BC的中点.
,M为BC的中点.
(1)证明:AM⊥PM;
(2)求二面角P-AM-D的大小;
(3)求点D到平面AMP的距离.
18.
|
(1)每天不超过20人排队结算的概率是多少?
(2)一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,商场就需要增加结算窗口,请问该商场是否需要增加结算窗口?
19. (本大题满分12分)已知中心在原点的椭圆C的左焦点为![]() ,右顶点为(2,0).
,右顶点为(2,0).
(1)求椭圆C的方程;
(2)若直线l:![]() 与椭圆C有两个不同的交点A和B,且
与椭圆C有两个不同的交点A和B,且![]() (其中O为原点), 求实数m的取值范围.
(其中O为原点), 求实数m的取值范围.
20. (本大题满分12分)已知曲线C:![]() ,过C上一点
,过C上一点![]() 作一斜率为
作一斜率为![]() 的直线交曲线C于另一点
的直线交曲线C于另一点![]() ,点列An(n=1,2,3,…)的横坐标构成数列
,点列An(n=1,2,3,…)的横坐标构成数列![]() ,其中
,其中![]() .
.
(1)求xn与xn+1的关系式;
(2)求证:![]() 是等比数列;
是等比数列;
(3)若![]() 为偶数,求证:-x1+x2-x3+x4-…+(-1)nxn<1.
为偶数,求证:-x1+x2-x3+x4-…+(-1)nxn<1.
21. (本大题满分14分)已知函数![]() 在区间(-∞,-2]上单调递增,在区间[-2,2]上单调递减,且b≥0.
在区间(-∞,-2]上单调递增,在区间[-2,2]上单调递减,且b≥0.
(1)求![]() 的表达式;
的表达式;
(2)设0<m≤2,若对任意的x1、x2∈[m-2,m],不等式![]() ≤16m恒成立,求实数m的最小值.
≤16m恒成立,求实数m的最小值.
襄樊市高三调研测试题(2006.4)
数学(文科)参考答案及评分标准
一.选择题:BDCBA CDCCB
二.填空题:11.6 12.(![]() ,1) 13.8 14.60 15.
,1) 13.8 14.60 15.![]()
三.解答题:
16.解:∵p与q是共线向量
∴(2-2sin A)(1+sin A)-(cos A+sin A)(sin A-cos A)=0 2分
整理得:![]() ,∴
,∴![]() 4分
4分
∵△ABC为锐角三角形,∴A=60° 6分
![]()
![]() 10分
10分
当B=60°时取函数取最大值2.
此时三角形三内角均为60° 12分
17.(1)证:以D点为原点,分别以直线DA、DC为x轴、y轴,建立的空间直角坐标系D-xyz,
则D(0,0,0),P(0,1,![]() ),C(0,2,0),A(
),C(0,2,0),A(![]() ,0,0),M(
,0,0),M(![]() ,2,0) 2分
,2,0) 2分
∴![]() (
(![]() ,1,
,1,![]() ),
),![]() (
(![]() ,2,0) 4分
,2,0) 4分
∴![]()
即![]() ,∴AM⊥PM. 6分
,∴AM⊥PM. 6分
(2)解:设n=(x,y,z),且n⊥平面PAM,则
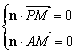 ,即
,即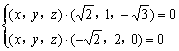
∴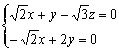 Þ
Þ 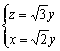
令y=1,得![]() ,得
,得![]() 8分
8分
取p=(0,0,1),显然p⊥平面ABCD
∴![]()
结合图形可知,二面角P-AM-D为45°; 10分
(3)解:设点D到平面PAM的距离为d,由(2)可知![]() 与平面PAM垂直,则
与平面PAM垂直,则
![]()
即点D到平面PAM的距离为![]() . 13分
. 13分
18.(1)解:每天不超过20人排队结算的概率为:P=0.1+0.15+0.25+0.25=0.75,即不超过20人排队结算的概率是0.75. 4分
(2)解:每天超过15人排队结算的概率为:0.25+0.2+0.05=![]() , 6分
, 6分
一周7天中,没有出现超过15人排队结算的概率为![]() ;
;
一周7天中,有一天出现超过15人排队结算的概率为![]() ;
;
一周7天中,有二天出现超过15人排队结算的概率为![]() ; 9分
; 9分
所以有3天或3天以上出现超过15人排队结算的概率为:
![]() ,
,
故该商场需要增加结算窗口. 12分
19.(1) 解:设椭圆方程为![]() (a>b>0)
(a>b>0)
由已知得a=2,c=![]() ,b=1
,b=1
故椭圆C的方程为![]() . 4分
. 4分
(2)将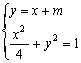 得
得![]()
由已知,![]() ,即m2<5 ① 8分
,即m2<5 ① 8分
设![]() ,则
,则![]()
![]()
而![]()
![]() 10分
10分
于是![]() ,即
,即![]() ②
②
由①、②得 ![]()
故m的取值范围为![]() 12分
12分
20.(1)解:由已知得:![]()
即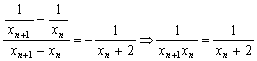
∴![]() 4分
4分
(2)证: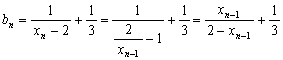
![]()
∴![]() 是等比数列 8分
是等比数列 8分
(3)证:由![]() 得:
得:![]()
∴![]() Þ
Þ ![]()
当![]() 为偶数时,
为偶数时,![]()
![]() 10分
10分
∴-x1+x2-x3+x4-…+(-1)nxn=(x2-x1)+(x4-x3)+…+ (xn-xn-1)
=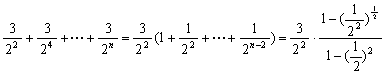
![]() 12分
12分
21.(1)解:f (x)=x3+bx2+cx+1,f ′ (x)=3x2+2bx+c
∵f (x)在区间(-∞,-2)上单调递增,在区间[-2,2]上单调递减,
∴方程f ′ (x)=3x2+2bx+c=0有两个不等实根x1、x2,且x1=-2,x2≥2 2分
∴![]() Þ b≤0
Þ b≤0
又已知b≥0,∴b=0
∴x2=2,c=-12,∴f (x)=x3-12x+1. 6分
(2)解:对任意的x1、x2∈[m-2,m],不等式 f (x1)-f (x2) ≤16m恒成立,等价于在区间[m-2,m]上,[f (x)]max-[f (x)]min≤16m 8分
f (x)=x3-12x+1,f ′(x)=3x2-12
由f ′ (x)=3x2-12<0解得-2<x<2
∴f (x)的减区间为[-2,2]
∵0<m≤2, ∴[m-2,m]![]() [-2,2]
[-2,2]
∴f (x)在区间[m-2,m]上单调递减, 10分
在区间[m-2,m]上,[f (x)]max=f (m-2)=(m-2)3-12(m-2)+1
[f (x)]min=f (m)=m3-12m-1 12分
[f (x)]max-f (x)]min=[(m-2)3-12(m-2)+1]-(m3-12m+1)=-6m2+12m+16
∵[f (x)]max-f (x)]min≤16m,∴-6m2+12m+16≤16m,3m2+2m-8≥0
解得m≤-2,或m≥![]() ,又0<m≤2,故mmin=
,又0<m≤2,故mmin=![]() . 14分
. 14分