叙永一中高2006级数学阶段测试题
(第一轮复习总结卷)2006.4.1
考试时间:120分钟 班级________姓名________学号__________
一. 选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案的标号字母填在题后的括号内)
1.![]() 的值为( )天((星教育网
的值为( )天((星教育网
A .-3 B.-1 C.1 D.3
2.函数![]() 的最小正周期为( )
的最小正周期为( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
3.已知向量![]() 且
且![]() 与
与![]() 平行,则
平行,则![]() 等于( )
等于( )
A.-6 B.6 C.4 D. -4
4.给出下列关于互不相同的直线m、l、n和平面α、β的四个命题:
①若![]() ;
;
②若m、l是异面直线,![]() ;
;
③若![]() ;
;
④若![]()
其中为假命题的是( )
A.① B.② C.③ D.④
5.一组数据的方差为2,将这组数据中每个扩大为原数的2倍,则所得新的一组数据的方差是( )
A.16 B.8 C.4 D.2
6.把语文、数学、物理、历史、外语这五门课程安排在一天的五节课里,如果数学必须比历史先上,则不同的排法有( )
A.48 B.24 C.60 D.120
7.设命题甲:平面内有两定点![]() 和动点P,使
和动点P,使![]() 是定值;命题乙:点P的轨迹是椭圆,则甲是乙的( )
是定值;命题乙:点P的轨迹是椭圆,则甲是乙的( )
A.充分但不必要条件B.必要但不充分条件C.充要条件D.既不充分也不必要条件
8.在(1-x)5+(1-x)6+(1-x)7+(1-x)8的展开式中,含x3的项的系数是( )
A. 74 B. 121 C. -74 D. -121
9.已知数列![]() 的通项公式为
的通项公式为![]() ,设其前n项和为Sn,则使
,设其前n项和为Sn,则使![]() 成立的自然数n( )
成立的自然数n( )
A.有最小值63 B.有最大值63 C.有最小值31 D.有最大值31
10.正四棱柱ABCD–A1B1C1D1中,AB=3,BB1=4.长为1的线段PQ在棱AA1上移动,长为3的线段MN在棱CC1上移动,点R在棱BB1上移动,则四棱锥R–PQMN的体积是( )
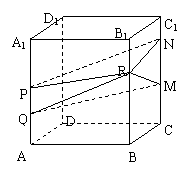 A.6 B.10 C.12 D.不确定
A.6 B.10 C.12 D.不确定
11.已知椭圆的离心率为e,两焦点分别为F1、F2,
抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,
若e|PF2|=|PF1|,则e的值为( )
A.![]() B.
B.![]() C.
C. ![]() D.以上均不对
D.以上均不对
12.对于集合![]() 、
、![]() ,定义
,定义![]() ,
, ![]() =
=![]()
![]()
![]() .设
.设![]() ,
,![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共4小题,每小题4分,共16分)
13.某中学有高一学生400人,高二学生300人,高三学生300人,现通过分层抽样取一个样本容量为n的样本,已知每个学生被抽到的概率为0.2,则n =______
14.若半径为R的球与正三棱柱的各个面相切,则球与正三棱柱的体积比是________.
15.实系数方程![]() 的两根为
的两根为![]() ,且
,且![]() ,则
,则![]() 的取值范围是
的取值范围是
16.已知定义在R上的函数y=f(x)满足以下三个条件:
(1)对任意的x∈R,都有f(x+4)=f(x);
(2)对任意的x1,x2∈R,且0≤x1<x2≤2,都有f(x1)<f(x2);
(3)函数y=f(x+2)的图像关于y轴对称.
则a=f(4.5),b=f(6.5),c=f(7)从小到大的关系是________.
三、解答题
17.(12分)已知向量m=(1,1),向量n与向量m的夹角为![]() ,且m·n=-1.
,且m·n=-1.
(1)求向量n;
(2)设向量a=(1,0),向量b=(cosx,2cos2(![]() )),其中0<x<
)),其中0<x<![]() ,若n·a=0,试求|n+b|的取值范围.
,若n·a=0,试求|n+b|的取值范围.
18.(12分)有红蓝两粒质地均匀的正方体形状骰子,红色骰子有两个面是8,四个面是2,蓝色骰子有三个面是7,三个面是1,两人各取一只骰子分别随机投掷一次,所得点数较大者获胜.
⑴分别求出两只骰子投掷所得点数的分布列及期望;⑵投掷蓝色骰子者获胜的概率是多少?
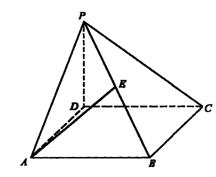
19.(12分)如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,PD⊥面AC,且
为正方形,PD⊥面AC,且![]() ,
,![]() 是
是![]() 的中点.
的中点.
 (1)求异面直线
(1)求异面直线![]() 、
、![]() 所成的角;
所成的角;
(2)在平面![]() 内求一点
内求一点![]() ,使得
,使得![]() 平面
平面![]() ;
;
(3)求二面角![]() 的大小.
的大小.
20.已知函数f(x)=(x2+![]() )(x+a)(a
)(x+a)(a![]() R)
R)
(1)若函数f(x)的图象上有与x轴平行的切线,求a的范围;
(2)若![]() (-1)=0,(I)求函数f(x)的单调区间;(II)证明对任意的x1、x2
(-1)=0,(I)求函数f(x)的单调区间;(II)证明对任意的x1、x2![]() (-1,0),不等式f(x1)-f(x2)<
(-1,0),不等式f(x1)-f(x2)<![]() 恒成立。
恒成立。
21.(12分)已知二次函数![]() 的图象过点
的图象过点![]() ,且
,且![]()
(1)求![]() 的解析式;
的解析式;
(2)若数列![]() 满足
满足![]() ,且
,且![]() ,求
,求![]() 的通项公式并证明
的通项公式并证明 ![]() .
.
22.(14分)已知双曲线的中心在原点,右顶点为A(1,0),点P、Q在双曲线的右支上,
点M(m,0)到直线AP的距离为1.
(1)若直线AP的斜率为k,且k∈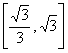 ,求实数m的取值范围;
,求实数m的取值范围;
(2)当m=![]() 时,△APQ的内心恰好是点M,求此双曲线的方程.
时,△APQ的内心恰好是点M,求此双曲线的方程.
参考答案
一、选择题(60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | A | D | C | B | C | B | D | A | A | C | C |
二、填空题(16分)
13.200
14.![]() 15.
15.![]() 16.a<c<b
16.a<c<b
三、解答题
17.解:(1)令n=(x,y),则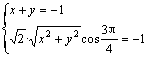
即![]() ,故n=(-1,0)或n=(0,-1)
,故n=(-1,0)或n=(0,-1)
(2)∵a=(1,0)n·a=0
∴n=(0,-1) n+b=![]()
故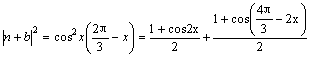 =1+
=1+![]()
![]() =1+
=1+![]()
![]() =1+
=1+![]()
∵0<x<![]()
则-1≤cos![]()
18.解:⑴红色骰子投掷所得点数为![]() 是随即变量,其分布如下:
是随即变量,其分布如下:

![]() 8 2
8 2
P ![]()
![]()
E![]() =8·
=8·![]() +2·
+2·![]() =4
=4
蓝色骰子投掷所得点数![]() 是随即变量,其分布如下:
是随即变量,其分布如下:

![]() 7 1
7 1
P ![]()
![]()
E![]() =7·
=7·![]() +1·
+1·![]() =4
=4
⑵∵投掷骰子点数较大者获胜,∴投掷蓝色骰子这若获胜,则投掷后蓝色骰子点数为7,
红色骰子点数为2,∴投掷蓝色骰子获胜概率是![]() =
=![]() ·
·![]() =
=![]()
19.解:(1)建立如图所示的空间直角坐标系,则A (a,0,0) , B(a,a,0),
C(0,a,0),P(0,0,a) ![]() 。
。![]()
![]() 。
。
![]() 。 又
。 又![]()
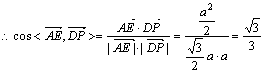 。故异面直线AE、DP所成角为
。故异面直线AE、DP所成角为![]() 。
。
(2)∵F∈平面PAD,故设F(x,0,z),则有![]() 。
。
∵EF⊥平面PBC,∴![]() 且
且![]() 。∴
。∴![]()
又![]() ,
,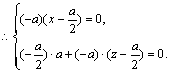
从而![]() ∴
∴![]() ,取AD的中点即为F点。
,取AD的中点即为F点。
(3)∵PD⊥平面ABCD, ∴CD是PC在平面ABCD上的射影。
又∵CD⊥BC,由三垂线定理,有PC⊥BC。取PC的中点G,连结EG,则EG//BC。
∴EG⊥PC。连结FG。∵EF⊥平面PBC,EG是FG在平面PBC上的射影,且PC⊥EG,∴FG⊥PC。∴∠FGE为二面角F―PC―E的平面角。![]() 。
。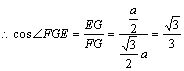 。∴二面角F―PC―E的大小为
。∴二面角F―PC―E的大小为![]() 。
。
20.解:![]() ,
,![]()
⑴![]() 函数
函数![]() 的图象有与
的图象有与![]() 轴平行的切线,
轴平行的切线,![]() 有实数解
有实数解
![]() ,
,![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]()
⑵![]() ,
,![]() ,
,![]() ,
,![]()
(Ⅰ)由![]() 或
或![]() ;由
;由![]()
![]() 的单调递增区间是
的单调递增区间是![]() ;单调减区间为
;单调减区间为![]()
(Ⅱ)易知![]() 的最大值为
的最大值为![]() ,
,![]() 的极小值为
的极小值为![]() ,又
,又![]()
![]() 在
在![]() 上的最大值
上的最大值![]() ,最小值
,最小值![]()
![]() 对任意
对任意![]() ,恒有
,恒有![]()
21.解:(1)![]() ;(2)
;(2)![]() ;
;
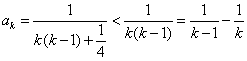 (
(![]() )当
)当![]() 时,显然成立;
时,显然成立;
当![]() 时,
时,![]() ;
;
22.解:(1)由条件得直线AP的方程为![]() ,即
,即![]() ,
,
∵点M到直线AP的距离为1,
∴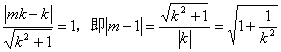 ,………………………………… 3分
,………………………………… 3分
∵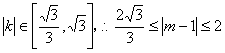 ,
,
即![]() ,或
,或![]() ,
,
∴m的取值范围是![]()
![]() .…………………………………… 6分
.…………………………………… 6分
(2)可设双曲线的方程为![]() ,……………………………………… 7分
,……………………………………… 7分
∵![]() ,
,
∵M是△APQ的内心,且M到直线AP的距离为1,∴∠MAP=45°,………… 9分
即直线AM是∠PAQ的角平分线,不妨设P在第一象限,
则直线AP、AQ的斜率分别为kAP=1,kAQ=-1,……………………………………… 10分
又由双曲线的对称性及点M到PQ的距离为1知直线PQ的方程为![]()
再联立直线AP的方程![]() 得点
得点![]() ,……………………… 11分
,……………………… 11分
将点P的坐标代入双曲线的方程得
![]() ,解得
,解得![]() ,……………………………… 12分
,……………………………… 12分
即![]()
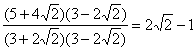 ,…………………………… 13分
,…………………………… 13分
∴双曲线的方程为![]() .………………………………………… 14分
.………………………………………… 14分