![]() 扬中市八桥中学高三数学期末复习练习050126
扬中市八桥中学高三数学期末复习练习050126
班级 姓名
一:选择题
1.若不等式∣ax + 2∣<6的解集为(-1,2),则实数a等于 【 】
A.-4 B.4 C.-8 D. 8
2.下列各组命题中,“![]() 或
或![]() ”形式的复合命题为假命题的是 【 】
”形式的复合命题为假命题的是 【 】
A.![]() :函数
:函数![]() 在
在![]() 上是增函数;
上是增函数;![]() :函数
:函数![]() 在
在![]() 上为奇函数;
上为奇函数;
B.![]() :导数为零的点一定是极值点;
:导数为零的点一定是极值点; ![]() :最大值点的导数一定为零;
:最大值点的导数一定为零;
C.![]() :互斥事件一定是对立事件;
:互斥事件一定是对立事件;![]() :对立事件一定是互斥事件;
:对立事件一定是互斥事件;
D.![]() :
:![]() ;
;![]() :
:![]()
3.已知函数y=3x4+1和y=4x3,它们的图象在公共点处的切线重合,则切线的斜率为
A、0 B、12 C、0或12 D、以上都不对 【 】
4.三个数![]() 成等比数列,若有
成等比数列,若有![]() 成立,则
成立,则![]() 的取值范围是 【 】
的取值范围是 【 】
A.
![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
5.现有200根相同的钢管,把它们堆放成正三角形垛,要使剩余的钢管最少,那么剩余
钢管的根数为 【 】
A.9 B.10 C.19 D.20
二:填空题
6.已知点![]() ,O为坐标原点,
,O为坐标原点,![]() , 若点P在第四象限内,则实数
, 若点P在第四象限内,则实数![]() 的取值范围是
。
的取值范围是
。
7.若函数![]() 在
在![]() 上存在反函数,则
上存在反函数,则![]() 的取值范围是
。
的取值范围是
。
8.F1,F2是双曲线![]() 的两个焦点,P是双曲线上的点,已知PF1,PF2,F1F2依次成等差数列,且公差大于0,则∠F1PF2=
.
的两个焦点,P是双曲线上的点,已知PF1,PF2,F1F2依次成等差数列,且公差大于0,则∠F1PF2=
.
9.若抛物线![]() 与其关于点(1,1)对称的抛物线有两个不同的交点,且过这两个交点的直线的倾斜角为45°,则实数a的值是
。
与其关于点(1,1)对称的抛物线有两个不同的交点,且过这两个交点的直线的倾斜角为45°,则实数a的值是
。
三:解答题
10.已知函数![]() 在[0,2]上有最小值8,求正数a的值.
在[0,2]上有最小值8,求正数a的值.
11.(12分)已知数列{an}的前n项和为Sn,且满足![]() .
.
(1)求证:{![]() }是等差数列;(2)求an的表达式;
}是等差数列;(2)求an的表达式;
(3)若bn=2(1-n)·an(n≥2)时,求证:b22+b32+…+bn2<1.
12.若![]() 的最小值为
的最小值为![]() .(1)求
.(1)求![]() 的表达式.
的表达式.
(2)求能使![]() 的
的![]() 值,并求出当
值,并求出当![]() 取此值时
取此值时![]() 的最大值.
的最大值.
13.某学生骑自行车上学,从家到学校的途中有2个交通岗.假设他在这两个交通岗处遇到红灯的事件是相互独立的,并且概率都是0.6.计算:
(Ⅰ)2次都遇到红灯的概率;
(Ⅱ)至少遇到1次红灯的概率.
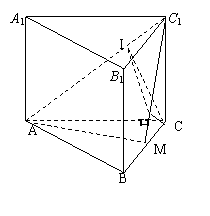
 14.如图,正三棱柱
14.如图,正三棱柱![]() 的底面边长为
的底面边长为![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() 是以点M为直角顶点的等腰直角三角形.
是以点M为直角顶点的等腰直角三角形.
(Ⅰ) 求证点![]() 为边
为边![]() 的中点;
的中点;
(Ⅱ) 求点![]() 到平面
到平面![]() 的距离;
的距离;
(Ⅲ) 求二面角![]() 的大小.
的大小.
参考答案
一、选择题:
ABBDB
二、填空题:
6.(-![]() ),7.
),7.![]() ,8.1200,9.2;
,8.1200,9.2;
三、解答题:
10.解:设![]() ,当x∈[0,2]时,可得
,当x∈[0,2]时,可得![]() .
.
(1) 若a>1时,则![]() ,解得a=16>1.
,解得a=16>1.
(2) 若0<a<1时,则![]() ,解得a=2,此与0<a<1矛盾,舍去.
,解得a=2,此与0<a<1矛盾,舍去.
故正数a =16.
11.证明:![]() ……1分
……1分
![]() ……2分 又
……2分 又![]()
![]() 是以2为首项,2为公差的等差数列……4分
是以2为首项,2为公差的等差数列……4分
(2)解:由(1)![]()
![]() ……5分 当n≥2时,
……5分 当n≥2时,
![]() (或n≥2时,
(或n≥2时,![]() )
)
当n=1时,![]() ………………7分
………………7分 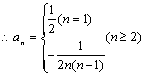 ………………8分
………………8分
(3)由(2)知,![]() ………………………………9分
………………………………9分
![]() …………………10分
…………………10分
![]() …………11分
…………11分 ![]() …………………………12分
…………………………12分
12. 解:(1)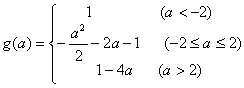
(2)当![]()
13.解:(Ⅰ)记“他第一次遇到红灯”为事件A,记“他第二次遇到红灯”为事件B.由题知,A与B是相互独立的,因此,“他两次都遇到红灯”就是事件A·B发生. 根据相互独立事件的概率乘法公式,得 P(A·B)=P(A)·P(B)=0.6×0.6=0.36.
答:他两次都遇到红灯的概率是0.36.
(Ⅱ)解法一:![]() =“他第一次没有遇到红灯”,
=“他第一次没有遇到红灯”,
![]() =“他第二次没有遇到红灯”.
=“他第二次没有遇到红灯”.
![]() “他第一次没有遇到红灯,第二次遇到红灯”,
“他第一次没有遇到红灯,第二次遇到红灯”,
![]() =“他第一次遇到红灯,第二次没有遇到红灯”,并有
=“他第一次遇到红灯,第二次没有遇到红灯”,并有![]() 与
与![]() 是互斥的,因此,他恰有一次遇到红灯的概率是
是互斥的,因此,他恰有一次遇到红灯的概率是
P(![]() +
+![]() )=P(
)=P(![]() )+P(
)+P(![]() )=(1-0.6)×0.6+0.6×(1-0.6)=0.48.
)=(1-0.6)×0.6+0.6×(1-0.6)=0.48.
![]() 他至少遇到1次红灯的概率是 P(A·B)+P(
他至少遇到1次红灯的概率是 P(A·B)+P(![]() +
+![]() )=0.36+0.48=0.84.
)=0.36+0.48=0.84.
答:至少遇到1次红灯的概率是0.84.
解法二:![]() =“他第一次没有遇到红灯”,
=“他第一次没有遇到红灯”,
![]() =“他第二次没有遇到红灯”.
=“他第二次没有遇到红灯”.
![]() “他两次没有遇到红灯”.
“他两次没有遇到红灯”.
P(![]() ·
·![]() )=P(
)=P(![]() )·P(
)·P(![]() )=(1-0.6)×(1-0.6)=0.16,
)=(1-0.6)×(1-0.6)=0.16,
∴他至少遇到1次红灯的概率是P=1-P(![]() ·
·![]() )=1-0.16=0.84.
)=1-0.16=0.84.
答:至少遇到1次红灯的概率是0.84.
14.解: (Ⅰ)∵△AMC1为以点M为直角顶点的等腰直角三角形,
∴![]() .
.
![]() 正三棱柱ABC-A1B1C1,
正三棱柱ABC-A1B1C1,
∴CC1⊥底面ABC且底面ABC为正三角形
∴![]() 在底面内的射影为
在底面内的射影为![]() ,
,![]() .
.
![]() 底面ABC为正三角形
∴点
底面ABC为正三角形
∴点![]() 为BC边的中点.
为BC边的中点.
(Ⅱ) 过点C作CH⊥MC1,,
 由(Ⅰ)知
由(Ⅰ)知![]() ,
,
∴![]()
![]()
![]() ,∴
,∴![]() ,
,
∴![]() ,
,
由(Ⅰ)知,![]() ,
,![]() 且
且![]() .
.
∴![]() .∴
.∴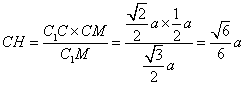 .
.
∴点![]() 到平面
到平面![]() 的距离为底面边长为
的距离为底面边长为![]() .
.
(Ⅲ) 过点![]() 作
作![]() ,
,![]()
![]() ,
,
∴![]() 为
为![]() 在平面
在平面![]() 内的射影,
内的射影,
∴![]() ,
,![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在直角三角形![]() 中,
中,
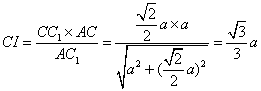 ,
, 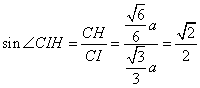 ,
,
∴![]() ,
,
∴二面角![]() 的大小为45O.
的大小为45O.