2006年高考预测
数学(文)试题
| 题 号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得 分 | |||||||||
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.第I卷为选择题,共12小题,60分;第II卷为填空题和解答题,共11小题,90分.全卷满分150分,考试时间120分钟.
 |
第Ⅰ卷 (选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一
项是符合题目要求的.请把所选项前的字母填在题后的括号内.
1.以下满足A![]() B的非空集合A、B的四个命题中正确的个数是 ( )
B的非空集合A、B的四个命题中正确的个数是 ( )
①若任取x∈A,则x∈B ②若x![]() A,则x∈B是必然事件
A,则x∈B是必然事件
③若任取x∈B,则x∈A是随机事件 ④若x![]() B,则x
B,则x![]() A是必然事件
A是必然事件
A.4 B.3 C.2 D.1
2.定义运算![]() ( )
( )
A.(0, 1) B.(-¥, 1) C.(0, 1) D.[1, +¥]
3.已知数列![]() 满足
满足![]() ,且
,且![]() ,其前
,其前![]() 项之和为
项之和为![]() ,则满足不等
,则满足不等
式![]() 的最小整数
的最小整数![]() 是 ( )
是 ( )
A.5 B.6 C.7 D.8
4.△ABC中,A>B,则下列四个不等式中恒成立的个数是 ( )
①sinA>sinB ②cosA<cosB ③sin2A>sin2B ④cos2A<cos2B
A.4个 B.3个 C.2个 D.1个
5.函数![]() 的图象只可能是 (
)
的图象只可能是 (
)
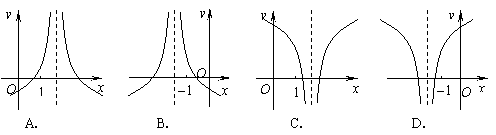
6.已知m、l是异面直线,有下面四个结论:
①必存在平面α过m且与l平行; ②必存在平面β过m且与l垂直;
③必存在平面γ与m、l都垂直; ④必存在平面π与m、l距离都相等.
其中正确的结论是 ( )
A.①② B.①③ C.②③ D.①④
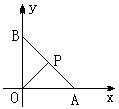
7.已知O为原点,点A,B的坐标分别为(a,0),(0,a),a是正的常数,点P在线
段AB上,且![]() ,则
,则![]() 的最大值是
( )
的最大值是
( )
A.a B.2a C.a2 D.3a
8.点![]()
![]()
![]() 所在平面区
所在平面区
域的面积是 ( )
A. 1 B. 2 C. 4 D.8
9.按照以下规律:
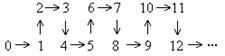
那么从![]() 到
到![]() 的顺序为
( )
的顺序为
( )
A.→ ↑ B.↑ → C.↓ → D.→ ↓
10.设![]() ,则
,则![]() = ( )
= ( )
A.256 B.96 C.128 D.112
11.下列三图中的多边形均为正多边形,M、N是所在边上的中点,双曲线均以图中的F1、
F2为焦点,设图①、②、③中的双曲线的离心率分别为e1,e2,e3,则 ( )
A.e1>e2>e3 B. e1<e2<e3 C. e1=e3<e2 D.e1=e3>e2
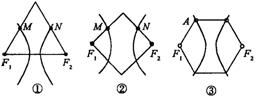 |
12.设![]() 是曲线
是曲线![]() 上的点C,F1(-4,0),F2(4,0),则 ( )
上的点C,F1(-4,0),F2(4,0),则 ( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
第Ⅱ卷(填空题和解答题,10小题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在题中横线上.
13.某中学的一个研究性学习小组共有10名同学,其中男生x名(3≤x≤9),现在从中选出
3人参加一次调查活动,若至少有1名女生去参加的概率为p,则p的最大值为_______.
14.给出下面的3个命题:(1)函数![]() 的最小正周期是
的最小正周期是![]() ;(2)函数
;(2)函数![]() 在区间
在区间![]() 上单调递增;(3)
上单调递增;(3)![]() 是函数
是函数![]() 的图象的一条对称轴.其中正确命题的序号是
.
的图象的一条对称轴.其中正确命题的序号是
.
15.已知凸函数的性质定理:如果函数f(x)在区间D上是凸函数,则对于区间内的任意![]() ,有
,有![]() ,已知y=sinx在区间(0,π)上是凸函数,那么在△ABC中,sinA+sinB+sinC的最大值为
.
,已知y=sinx在区间(0,π)上是凸函数,那么在△ABC中,sinA+sinB+sinC的最大值为
.
16.已知![]() ,
, ![]() ,
, ![]() . 若将坐标平面沿x轴折成直二面角, 则折后
. 若将坐标平面沿x轴折成直二面角, 则折后
![]() 的余弦值为
.
的余弦值为
.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)在![]() 中,
中,![]() 所对的边长分别为
所对的边长分别为![]() ,设
,设
![]() 满足条件
满足条件![]() 和
和![]() ,求
,求![]() 和
和![]() 的值.
的值.
18.(本小题满分12分)一位学生每天骑自行车上学, 从他家到学校有5个交通岗, 假设他在
交通岗遇到红灯是相互独立的, 且首末两个交通岗遇到红灯的概率均为p , 其余3个交通
岗遇到红灯的概率均为![]() .
.
(I) 若![]() , 求该学生在第三个交通岗第一次遇到红灯的概率;
, 求该学生在第三个交通岗第一次遇到红灯的概率;
(II) 若该学生至多遇到一次红灯的概率不超过![]() , 求p的取值范围.
, 求p的取值范围.
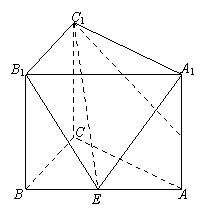
19.(本小题满分12分)如图,已知直三棱柱ABC—A1B1C1的侧棱长为2,底面△ABC是等
腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
(Ⅰ)求异面直线AB和C1D所成的角(用反三角函数表示);
(Ⅱ)若E为AB上一点,试确定点E在AB上的位置,使得A1E⊥C1D;
(Ⅲ)在(Ⅱ)的条件下,求点D到平面B1C1E的距离.
20.(本小题满分12分)已知函数![]() ,
,
(I)求函数![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(II)过点![]() 作曲线
作曲线![]() 的切线,求此切线的方程.
的切线,求此切线的方程.
21.
(本小题满分12分)已知函数![]() 数列
数列![]() 中,
中, ![]()
![]() . 当a取不同的值时,得到不同的数列
. 当a取不同的值时,得到不同的数列![]() , 如当
, 如当![]() 时, 得到无穷数列
时, 得到无穷数列![]() 当
当![]() 时, 得到有穷数列
时, 得到有穷数列![]()
(I) 求a的值, 使得![]() ;
;
(II) 设数列![]() 满足
满足![]()
求证: 不论a取![]() 中的任何数, 都可以得到一个有穷数列
中的任何数, 都可以得到一个有穷数列![]() ;
;
(III) 求a的取值范围, 使得当![]() 时, 都有
时, 都有![]() .
.
22.(本小题满分14分)在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 满足
满足
![]() ,
,![]()
(I)当![]() 变化时,求点
变化时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(II)若过点![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两点,求证:直线
两点,求证:直线![]() 的斜率依次成
的斜率依次成
等差数列.
文科数学参考答案
一、选择题:本题考查基本知识和基本运算.每小题5分,满分60分.
1.解:B.根据A![]() B的意义,以及必然事件、不可能事件、随机事件的概念,可知①③
B的意义,以及必然事件、不可能事件、随机事件的概念,可知①③
④正确,选B.
2.解:C. ![]() ,
,
故![]() 的取值范围是
的取值范围是![]() .选C.
.选C.
评:正确理解函数的定义,结合常见的函数图象来得到值域是解决本题的关键.本题实际上就是求函数![]() 的值域.
的值域.
3.解:C. 设![]() ,则
,则![]()
![]() ,
,
![]() 是以8为首项,
是以8为首项,![]() 为公比的等比数列,
为公比的等比数列,![]() ,不等式可化为
,不等式可化为![]() ,
,
最小整数![]() 是7. 选C.
是7. 选C.
4.解:B.①成立,![]() .
.
②成立,因为![]() 在
在![]() 上是减函数,∴
上是减函数,∴![]() .
.
③不成立,可举反例,![]() ,
,![]() ,
,![]() .
.
∴③不对.
④成立,∵![]() ,∴正确.
,∴正确.
或者![]()
故选B.
5.解:B. ![]() ,由图象可知
,由图象可知
![]() .故
.故![]() .由函数单调性知选B.
.由函数单调性知选B.
 6.解:D. 对于②若m、l不垂直,则满足条件的平面不存在.对于③m、l应为平行线.
6.解:D. 对于②若m、l不垂直,则满足条件的平面不存在.对于③m、l应为平行线.
①④可推出,故选D.
7.解:C. ![]()
由图可知,当P与A重合,![]() ,选C.
,选C.
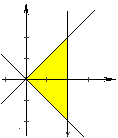 8.解:C.设
8.解:C.设![]() ,则
,则![]() 即
即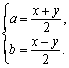
据题意,有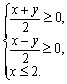 即
即 如图,故选C.
如图,故选C.
9.解:C. 观察↓→处可见均为4的倍数,从而2004也在此位置,所以2003到2005的顺
序为↓→,所以选C.
10.解:D. 与二项式定理有关的问题,常常需进行合理的赋值,在本题中,分别令![]() ,可求出结果,选D.
,可求出结果,选D.
11. 解:D. 由图知显然①与③是同一曲线,不妨令|F1F2|=1,则①中|MF1|=![]() ,
,
c1=![]() ,|MF2|=
,|MF2|=![]() ,a1=
,a1=![]() e1=
e1=![]() +1,而②c=
+1,而②c=![]() ,
,
|MF2|=![]() ,
,
∴e2=![]() <e1, ∴e1=e3>e2.答案:D.
<e1, ∴e1=e3>e2.答案:D.
12.解:A. 曲线![]() 可化简为
可化简为![]() ,它表示椭圆
,它表示椭圆![]() 内的一个菱形及其内部,故曲线上点满足PF1+PF2≤10,选A.
内的一个菱形及其内部,故曲线上点满足PF1+PF2≤10,选A.
二、填空题:本题考查基本知识和基本运算.每小题4分,满分16分.
13. 解:![]() .提示:由题意,
.提示:由题意,![]() ,要使p最大,只要
,要使p最大,只要![]() 最小,则x要最小,即x=3.∴此时p=
最小,则x要最小,即x=3.∴此时p=![]() .
.
14. 解:①②.提示:③中![]() 是
是![]() 的对称中心.
的对称中心.
15.解:![]() .提示:
.提示:![]() .
.
16.解:![]() .提示:画好图象,注意折叠前后的不变量和改变量。
.提示:画好图象,注意折叠前后的不变量和改变量。
三、解答题:本大题考查分析问题和解决问题的能力.共6小题,满分共74分.
17.本小题主要考查余弦定理、正弦定理,三角函数的恒等变形等基本解题方法.
满分12分.
解:由余弦定理![]() ,因此
,因此![]() .……………4分
.……………4分
在![]() 中,
中,![]() . ……………6分
. ……………6分
由已知条件,应用正弦定理
![]() ,
,
……………10分
解得![]() ,从而
,从而![]() .
……………12分
.
……………12分
18.本小题主要考查概率的基础知识,以及运用概率知识解答实际问题的能力.满分12分.
解: (I) 记该学生在第![]() 个交通岗遇到红灯
个交通岗遇到红灯![]()
![]() ,
,
![]()
答:该学生在第三个交通岗第一次遇到红灯的概率为![]() ……………6分
……………6分
(II) 该学生至多遇到一次红灯指没有遇到红灯(记为A)或恰好遇到一次红灯(记为B)
![]() ……………7分
……………7分
![]()
![]() …………………9分
…………………9分
![]()
![]() ……………11分
……………11分
又![]() 所以p的取值范围是
所以p的取值范围是![]() ……………12分
……………12分
19.本小题主要考查直三棱锥、异面直线的角、线线垂直、点面距离等基础知识,同时考
查空间想像能力和推理、运算能力.满分12分.
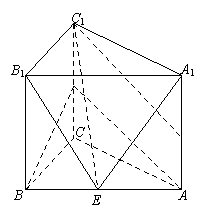 解(Ⅰ)法一:取CC1的中点F,连接AF,BF,则AF∥C1D.
解(Ⅰ)法一:取CC1的中点F,连接AF,BF,则AF∥C1D.
∴∠BAF为异面直线AB与C1D所成的角或其补角.…1'
∵△ABC为等腰直角三角形,AC=2,∴AB=![]() .
.
又∵CC1=2,∴AF=BF=![]() .
.
∵cos∠BAF=![]() ,…………3'
,…………3'
∴∠BAF=![]() ,
,
即异面直线AB与C1D所成的角为
![]() .…………………………4'
.…………………………4'
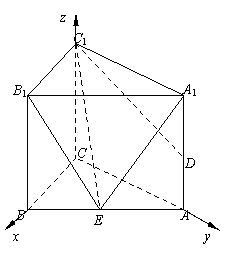
法二:以C为坐标原点,CB,CA,CC1分别为x轴,
y轴,z轴建立空间直角坐标系,
则A(0,2,0),B(2,0,0),
C1(0,0,2),D(0,2,1),
∴![]() =(2,-2,0),
=(2,-2,0),![]() =(0,2,-1).
=(0,2,-1).
由于异面直线AB与C1D所成的角
为向量![]() 与
与![]() 的夹角或其补角.…………1'
的夹角或其补角.…………1'
设![]() 与
与![]() 的夹角为
的夹角为![]() ,
,
 则cos
则cos![]() =
=![]() =
=![]() ,…………3'
,…………3'
∴![]() =
=![]() ,
,
即异面直线AB与C1D所成的角为
![]() .………………4'
.………………4'
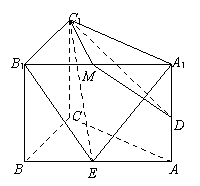
(Ⅱ)法一:过C1作C1M⊥A1B1,垂足为M,
则M为A1B1的中点,且C1M⊥平面AA1B1B.连接DM.
 ∴DM即为C1D在平面AA1B1B上的射影.…6'
∴DM即为C1D在平面AA1B1B上的射影.…6'
要使得A1E⊥C1D,
由三垂线定理知,只要A1E⊥DM. ………7'
∵AA1=2,AB=2![]() ,
,
由计算知,E为AB的中点. ……………8'
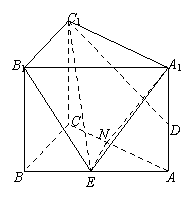
法二:过E作EN⊥AC,垂足为N,则EN⊥平面AA1C1C.
连接A1N.
∴A1N即为A1E在平面AA1C1C上的射影.………6'
要使得A1E⊥C1D,
由三垂线定理知,只要A1N⊥C1D.……………7'
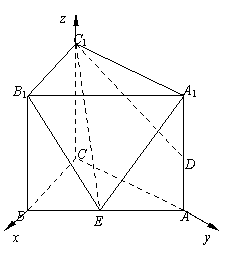 ∵四边形AA1C1C为正方形,
∵四边形AA1C1C为正方形,
∴N为AC的中点,
∴E点为AB的中点.…………………………8'
法三:以C为坐标原点,CB,CA,CC1分别为x轴,
y轴,z轴建立空间直角坐标系,
则A1(0,2,2),B(2,0,0),
C1(0,0,2), D(0,2,1),
设E点的坐标为(x,y,0),
要使得A1E⊥C1D,
只要![]() ·
·![]() =0,………………………6'
=0,………………………6'
∵![]() =(x,y-2,-2),
=(x,y-2,-2),
![]() =(0,2,-1),
=(0,2,-1),
∴y=1.……………………………………7'
又∵点E在AB上,∴![]() ∥
∥![]() .∴x=1.
.∴x=1.
∴E点为AB的中点.……………………8'
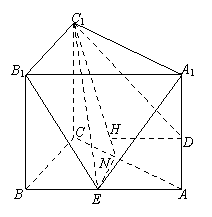
(Ⅲ)法一:取AC中点N,连接EN,C1N,
则EN∥B1C1.
∵B1C1⊥平面AA1C1C,
∴面B1C1NE⊥平面AA1C1C.
过点D作DH⊥C1N,垂足为H,
则DH⊥平面B1C1NE,
∴DH的长度即为点D到
 平面B1C1E的距离.…………………10'
平面B1C1E的距离.…………………10'
在正方形AA1C1C中,由计算知DH=![]() ,
,
即点D到平面B1C1E的距离为![]() .………12'
.………12'
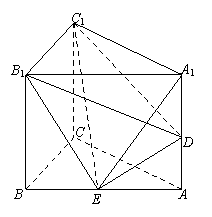
法二:连接DE,DB1.
在三棱锥D—B1C1E中,点C1到平面DB1E的距离
为![]() ,B1E=
,B1E=![]() ,DE=
,DE=![]() ,
,
又B1E⊥DE,∴△DB1E的面积为![]() ,
,
∴三棱锥C1—DB1E的体积为1.……10'
设点D到平面B1C1E的距离为d,在△B1C1E中,B1C1=2,B1E= C1E=![]() ,
,
∴△B1C1E的面积为![]() .由
.由![]() ,
,
得d=![]() ,即点D到平面B1C1E的距离为
,即点D到平面B1C1E的距离为![]() .………………………12'
.………………………12'
20.本小题主要考查导数的基础知识及其应用,以及综合应用知识分析问题和解决问题的
能力.满分12分.
解:(I)![]() ,
……………………………………………2分
,
……………………………………………2分
当![]() 或
或![]() 时,
时,![]() ,
,
![]() 为函数
为函数![]() 的单调增区间 …………………………………………3分
的单调增区间 …………………………………………3分
当![]() 时,
时,![]() ,
,
![]() 为函数
为函数![]() 的单调减区间
………………………………………………4分
的单调减区间
………………………………………………4分
又因为![]() ,
,
所以当![]() 时,
时,![]() ………………………………………………5分
………………………………………………5分
当![]() 时,
时,![]() ………………………………………………6分
………………………………………………6分
(II)设切点为![]() ,则所求切线方程为
,则所求切线方程为
![]() ………………………………………………8分
………………………………………………8分
由于切线过点![]() ,
,![]() ,
,
解得![]() 或
或![]() .
………………………………………………10分
.
………………………………………………10分
所以切线方程为![]() ,即
,即
![]() 或
或![]() .
…………………………………………12分
.
…………………………………………12分
21.本小题主要考查数列和不等式等数学知识的综合运用,以及代数推理能力、分析问题
和解决问题的能力,考查数学的基本思想和综合解答问题的能力.满分12分.
解: (I) 因为![]()
![]()
所以![]()
![]() ……………2分
……………2分
要![]() 即要
即要![]() . 所以,
. 所以, ![]() 时,
时, ![]() ……………4分
……………4分
(II)由题知![]()
![]() 不妨设a取
不妨设a取![]() ,
,
所以![]()
![]() ……………6分
……………6分
……,
![]() 所以
所以![]() ……………8分
……………8分
所以不论a取![]() 中的任何数, 都可以得到一个有穷数列
中的任何数, 都可以得到一个有穷数列![]() .……………9分
.……………9分
(III) ![]() ……………11分
……………11分
因为![]()
![]()
![]() , 所以只要有
, 所以只要有![]() 就有
就有![]() ………12分
………12分
由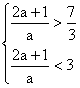 , 解得:
, 解得: 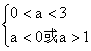 , 即
, 即![]() .
.
所以, a的取值范围是![]() .……………14分
.……………14分
22.本小题主要考查向量、轨迹和等差数列等数学知识的综合运用,考查数学的推理能
力、分析问题和解决问题的能力以及基本数学思想和综合解答问题的能力.满分14分.
(I)解:设点![]() 的坐标为
的坐标为![]() ,
,
由![]() ,得点
,得点![]() 是线段
是线段![]() 的中点,则
的中点,则![]() ,
,![]() ,…1分
,…1分
又![]() , ……………………………2分
, ……………………………2分
由![]() ,得
,得![]() ,
①…………………………………4分
,
①…………………………………4分
由![]() ,得
,得![]() ②…………………………5分
②…………………………5分
由①②消去![]() ,得
,得![]() 即为所求点
即为所求点![]() 的轨迹
的轨迹![]() 的方程 …………………………6分
的方程 …………………………6分
(II)证明:设直线![]() 的斜率依次为
的斜率依次为![]() ,并记
,并记![]() ,
,![]() ,
,
则![]() ……………………………………………………………………7分
……………………………………………………………………7分
设直线![]() 方程为
方程为![]()
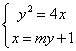 ,得
,得![]() ,
…………………………………………8分
,
…………………………………………8分
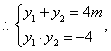 …………………………………………………9分
…………………………………………………9分
![]() ,
……………………………………10分
,
……………………………………10分
![]() ……………………………………11分
……………………………………11分
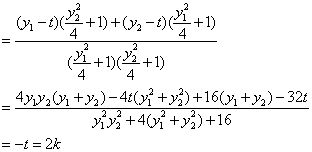
![]() 成等差数列
………………………………………………………………14分
成等差数列
………………………………………………………………14分