高级中学2004届普通毕业班综合测试六
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1、已知全集![]() ,集合
,集合![]() ,
,![]() ,则
,则![]() 为( )
为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、等差数列![]() 共有
共有![]() 项,其中奇数项的和为90,偶数项的和为72,且
项,其中奇数项的和为90,偶数项的和为72,且![]() ,则该数列的公差为 ( )
,则该数列的公差为 ( )
A、3 B、![]() C、
C、![]() D、
D、![]()
3、函数![]() 的单调递增区间是( )
的单调递增区间是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、函数![]() 的反函数是( )
的反函数是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5、过点![]() 作直线,使其在两坐标轴上的截距相等,则满足条件的直线的斜率为( )
作直线,使其在两坐标轴上的截距相等,则满足条件的直线的斜率为( )
A、![]() B、±1 C、
B、±1 C、![]() 或2 D、±1或2
或2 D、±1或2
6、不等式![]() 在
在![]() 上恒成立,则实数a的取值范围是( )
上恒成立,则实数a的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、在等差数列{![]() }中,若
}中,若![]() ,则
,则![]() 的值为( )
的值为( )
A、20 B、22 C、24 D、28
8、2个好朋友一起去一家公司应聘,公司人事主管通知他们面试时间的时候说:“我们公司要从面试的人中招3个人,你们同时被招聘进来的概率是![]() ”。根据他的话可推断去面试的人有( )个.
”。根据他的话可推断去面试的人有( )个.
A、70 B、21 C、42 D、35
 9、
9、![]() ( )
( )
A、![]() B、0 C、
B、0 C、![]() D、
D、![]()
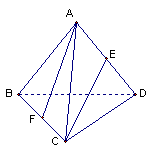
10、如图:在棱长都相等的四面体![]() 中,
中,![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() ,则直线
,则直线![]() 、
、![]() 所成角的余弦值为( )
所成角的余弦值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、已知双曲线的中心在原点,两个焦点为![]() 和
和![]() ,P在双曲线上,满足
,P在双曲线上,满足![]() 且△F1PF2的面积为1,则此双曲线的方程是( )
且△F1PF2的面积为1,则此双曲线的方程是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、北京市为成功举办2008年奥运会,决定从2003年到2007年5年间更新市内现有的全部出租车.若每年更新的车辆数比前一年递增10%,则2003年应更新现有车辆总数的(必要时,可参考1.14≈1.46;1.15≈1.61) ( )
A、10% B、16.4% C、16.7% D、20%
二、填空题:把答案填在题中横线上.
13、等差数列{an}中,若a1+a4+a7=15,a3+a6+a9=3,则S9= .
14、![]() 分别表示等比数列
分别表示等比数列![]() 的前
的前![]() 项、前
项、前![]() 项、前
项、前![]() 项的和,若
项的和,若![]() ,
,![]() 等于
(用
等于
(用![]() 表示).
表示).
15、过点![]() 的直线
的直线![]() 将圆:
将圆:![]() 分成两段弧,当其中的劣弧最短时,直线
分成两段弧,当其中的劣弧最短时,直线![]() 的方程为
_____
__ .
的方程为
_____
__ .
16、给出下列四个命题:① 函数![]() 为奇函数的充要条件是
为奇函数的充要条件是![]() =0;②函数
=0;②函数![]() 的反函数是
的反函数是![]() ;③若函数
;③若函数![]() 的值域是R,则
的值域是R,则![]() 或
或![]() ; ④ 若函数
; ④ 若函数![]() 是偶函数,则函数
是偶函数,则函数![]() 的图象关于直线
的图象关于直线![]() 对称。其中所有正确命题的序号是
.
对称。其中所有正确命题的序号是
.
三、解答题:解答应写出文字说明,证明过程或演算步骤.
17、已知函数![]()
(Ⅰ)求![]() 的最小正周期;
的最小正周期;
(Ⅱ)求![]() 的单调递减区间;
的单调递减区间;
(Ⅲ)函数![]() 的图象经过怎样的平移才能使所得图象对应的函数成为奇函数?
的图象经过怎样的平移才能使所得图象对应的函数成为奇函数?
18、已知:![]() 、
、![]() 、
、![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中![]()
(Ⅰ)若![]() ,且
,且![]() ,求
,求![]() 的坐标;
的坐标;
(Ⅱ)若![]() 且
且![]() 与
与![]() 垂直,求
垂直,求![]() 与
与![]() 的夹角θ.
的夹角θ.
19、求曲线![]() 与直线
与直线![]() 垂直的切线方程.
垂直的切线方程.
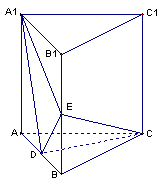 20、如图:直三棱柱
20、如图:直三棱柱![]() 中,
中,![]() ,
,![]() 。
。![]() 为
为![]() 的中点,
的中点,![]() 点在
点在![]() 上且
上且![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
21、设a>0,且a≠1. 给定下列两个命题:
P:函数![]() 在定义域上单调递增;
在定义域上单调递增;
Q:不等式![]() 的解集为
的解集为![]() .
.
若P、Q有且只有一个正确,求实数a的取值范围.
22、在平面直角坐标系中,![]() 为坐标原点,已知两点
为坐标原点,已知两点![]() 、
、![]() ,若点
,若点![]() 满足
满足![]() (
(![]() ),点
),点![]() 的轨迹与抛物线:
的轨迹与抛物线:![]() 交于
交于![]() 、
、![]() 两点.
两点.
(Ⅰ)求证:![]() ;
;
(Ⅱ)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得过点
,使得过点![]() 任作抛物线的一条弦,并以该弦为直径的圆都过原点。若存在,请求出
任作抛物线的一条弦,并以该弦为直径的圆都过原点。若存在,请求出![]() 的值及圆心的轨迹方程;若不存在,请说明理由.
的值及圆心的轨迹方程;若不存在,请说明理由.
高级中学2004届普通毕业班综合测试六参考答案
一、选择题:CBBCC CCBAC CB
二、填空题: 13、27 14、![]() 15、
15、![]() 16、①②③
16、①②③
三、解答题:
17、解:(Ⅰ)由![]()
由![]()
![]()
∴函数![]() 的最小正周期T=
的最小正周期T=![]()
(Ⅱ)由![]()
∴![]() 的单调递减区间是
的单调递减区间是![]()
![]() .
.
(Ⅲ)![]() ,∴奇函数
,∴奇函数![]() 的图象左移
的图象左移![]() 即得到
即得到![]() 的图象,
的图象,
故函数![]() 的图象右移
的图象右移![]() 个单位后对应的函数成为奇函数. (注:第Ⅲ问答案不唯一)
个单位后对应的函数成为奇函数. (注:第Ⅲ问答案不唯一)
18、解:(Ⅰ)设![]() ,
, ![]()
![]()
由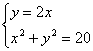 得
得 ![]() 或
或 ![]()
∴![]()
(Ⅱ)![]()
![]()
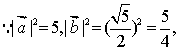 代入(※)中,
代入(※)中,
![]()
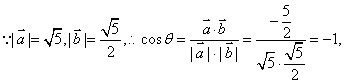
![]()
19、解:∵直线![]() 的斜率为
的斜率为![]() ,∴切线的斜率为2
,∴切线的斜率为2
又![]() ,∴
,∴![]()
∴切线方程为![]()
20、解:1)证:依题意知![]() ,
,![]() 且
且
![]() 为
为![]() 的中点,则
的中点,则![]() 也为
也为![]() 中点, ∴
中点, ∴![]()
又∵三棱柱![]() 为直三棱柱, ∴
为直三棱柱, ∴![]()
又![]() 且
且 ![]() 、
、![]() ,
故
,
故 ![]() .
.
2)解:由1)知![]() ,在
,在![]() 中过
中过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
连![]() ,由三垂线定理有
,由三垂线定理有![]() 为所求二面角得平面角
为所求二面角得平面角
易知![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]()
故![]()
![]()
在![]() 中
中 ![]() , 故所求二面角的大小为
, 故所求二面角的大小为![]() .
.
21、解:若命题P成立,即函数![]() 在定义域上单调递增,∴
在定义域上单调递增,∴![]()
若命题Q成立,即不等式![]() 的解集为
的解集为![]()
①当![]() 时,原式变为
时,原式变为![]() ,不等式的解集为
,不等式的解集为![]() ,
,
②当![]() 时,由不等式
时,由不等式![]() 的解集为
的解集为![]() ,
,
可得![]()
∴若命题Q成立,则有![]() 。
。
∴要使命P或Q有且只有一个成立,则![]() 的取值范围是
的取值范围是![]() 。
。
22、解:(Ⅰ)解:由![]() (
(![]() )知点
)知点![]() 的轨迹是
的轨迹是![]() 、
、![]() 两点所在的直线,故 点
两点所在的直线,故 点![]() 的轨迹方程是:
的轨迹方程是:![]() 即
即![]()
由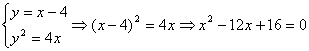
∴![]()
![]()
∴![]()
∴![]() 故
故 ![]()
(Ⅱ)解:存在点![]() ,使得过点
,使得过点![]() 任作抛物线的一条弦,以该弦为直径的圆都过原点
任作抛物线的一条弦,以该弦为直径的圆都过原点
由题意知:弦所在的直线的斜率不为零
故设弦所在的直线方程为:![]() 代入
代入 ![]() 得
得 ![]()
∴ ![]()
![]()
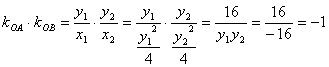
∴![]() 故以
故以![]() 为直径的圆都过原点
为直径的圆都过原点
设弦![]() 的中点为
的中点为![]() 则
则![]()
![]()
![]()
∴弦![]() 的中点
的中点![]() 的轨迹方程为:
的轨迹方程为: 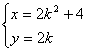 消去
消去![]() 得
得 ![]() .
.