曲阜师大附中2006届高三期末统考
数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分.考试时间120分钟.
第Ⅰ卷 (选择题共60分)
一、选择题:本大题共12小题,每小题5分,共60贫,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集![]()
![]()
![]() 则
则![]() 等于
等于
A.(2,4) B.(2,4] C.(2,3)![]() (3,4)
D.(2,3)
(3,4)
D.(2,3)![]() (3,4]
(3,4]
2.(理科学生做)在下列电路图中,表示开关A闭合是灯炮B亮的必要但不充分条件的是
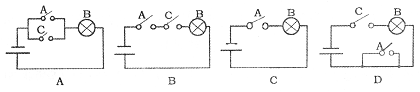 |
(文科学生做)设P、g为简单命题,则“P且q”为假是“P或q”为假的
A.必要不充分条件 B.充分不必要条件
C.充分条件 D.既不充分也不必要条件
3.在等差数列![]() 中,若
中,若![]() 则
则![]() 等于
等于
A.45 B.75 C.180 D.300
4.若函数![]() 为R上的奇函数,则函数
为R上的奇函数,则函数![]() 的图象,关于点( )对称
的图象,关于点( )对称
A.(O,0) B.(2,一3) C.(一2,一3)D.(2,3)
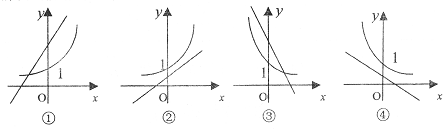 |
5.(理科学生做)若
A.①② B.③④ C.①③ D.②④
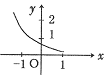 (文科学生做)函数
(文科学生做)函数![]() 的图象如右图,其中
的图象如右图,其中![]() 为常数,则下列结论正确的是
为常数,则下列结论正确的是
A.a>1,b<0 B.a>1,b>0
C.0<a<1,b<0 D.0<a<1,b>0
6.已知![]() ,则下列关系中必定成立的是
,则下列关系中必定成立的是
![]()
![]()
![]()
![]()
![]()
7.若关于![]() 的不等式
的不等式![]() 的解集是(1,+∞),则关于x的不等式
的解集是(1,+∞),则关于x的不等式![]() 的解集是
的解集是
A.(一∞,一1)![]() (2,+∞) B.(一1,2)
(2,+∞) B.(一1,2)
C.(1,2)
D.(一∞,1)![]() (2,+
(2,+![]() )
)
8.一条信息,若1人得知后用1小时将信息传给2人,这2人又用1小时分别传给未知
此信息的2人,如此继续下去,要传遍100万人口的城市,所需的时间大约是
A.1个月 B.10天 C.2天 D.1天
9.曲线![]() 和直线
和直线![]() 在y轴右侧的交点按横坐标从小到大依次设为
在y轴右侧的交点按横坐标从小到大依次设为![]() …,则
…,则![]() 等
等
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.(理科学生做)已知0是![]() 所在平面上一点,若
所在平面上一点,若![]() , 则O是
, 则O是![]() 的
的
A.垂心 B.重心 C.外心 D.内心
(文科学生做)若![]() 且
且![]() 则向量
则向量![]() 与b的夹角为
与b的夹角为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.如果直线l沿![]() 轴负方向平移5个单位,再沿
轴负方向平移5个单位,再沿![]() 轴正方向平移一个单位后,又回到原来的位置,那么直线
轴正方向平移一个单位后,又回到原来的位置,那么直线![]() 的斜率是
的斜率是
A.![]() B.
B.![]() C.
C.![]() D.5
D.5
12.(理科学生做)定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且在[一3,一2]上是减函数,若
,且在[一3,一2]上是减函数,若![]()
![]() 是锐角三角形的两个内角,则有
是锐角三角形的两个内角,则有
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(文科学生做)若函数![]() 是定义在
是定义在![]() 上的偶函数,在
上的偶函数,在![]() 上是减函数且
上是减函数且![]() ,则使得
,则使得![]() 的
的![]() 的取值范围是
的取值范围是
![]()
![]()
![]()
![]()
![]()
第Ⅱ卷(选择题共90分)
| 题号 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
二、填空题:本大题共4小题,每小题4分。共16分,把答案填在题中横线上.
13.已知实数![]() 满足不等式组
满足不等式组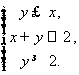 ,那么目标函数
,那么目标函数![]() 的最大值是
的最大值是
。
14.不等式![]() 的解集是
。
的解集是
。
15.将函数![]() 的图象按向量
的图象按向量![]() 平移得到
平移得到![]() 的图象,则
的图象,则![]() =
。(写出一个符合条件的向量。即可)
=
。(写出一个符合条件的向量。即可)
16.数列![]() 的首项为
的首项为![]() 且
且![]() ,设
,设![]() 为数列
为数列![]() 的前n项和,则
的前n项和,则![]() 。
。
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知![]()
(I)当向量![]() 与向量
与向量![]() 垂直时,求实数
垂直时,求实数![]() 的值﹔
的值﹔
(Ⅱ)当向量![]() 与向量
与向量![]() 平行时,求实数
平行时,求实数![]() 的值.
的值.
18.(本小题满分12分)
设![]() 为等比数列,
为等比数列,![]() ,已知
,已知![]()
(Ⅰ)求数列![]() 的首项和公比;
的首项和公比;
(Ⅱ)求数列![]() 的通项公式。
的通项公式。
19.(本小题满分12分)
已知在![]() 中,
中,![]()
求角![]() 、
、![]() 、
、![]() 的大小.
的大小.
20. (本小题满分12分)
设函数![]() 其中
其中![]() 为常数.
为常数.
(Ⅰ)解不等式![]()
(Ⅱ)试推断函数![]() 是否存在最小值,若存在,求出最小值;若不存在,说明理由.
是否存在最小值,若存在,求出最小值;若不存在,说明理由.
21.(本小题满分12分)
某市现有从事第二产业人员100万人,平均每人每年创造产值a万元(a为正常数),现在决定从中分流x万人去加强第三产业.分流后,继续从事第二产业的人员平均每人每年创造产值可增加![]() .而分流出的从事第三产业的人员平均每人每年可创造产值1.2a万元.在保证第二产业的产值不减少的情况下,分流出多少人,才能使该市第二、三产业的总产值增加最多?
.而分流出的从事第三产业的人员平均每人每年可创造产值1.2a万元.在保证第二产业的产值不减少的情况下,分流出多少人,才能使该市第二、三产业的总产值增加最多?
22. (本小题满分12分)
如果函数![]() 满足
满足![]() 且
且![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)是否存在各项均不为零的数列![]() 满足
满足![]() 为该数列的前
为该数列的前![]() 项和),如果存在,写出数列的一个通项公式
项和),如果存在,写出数列的一个通项公式![]() ,并说明满足条件的数列是
,并说明满足条件的数列是![]() 否唯一确定;如果不存在,请说明理由.
否唯一确定;如果不存在,请说明理由.
高三数学参考答案及评分意见
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | 理B 文A | C | D | 理D 文C | B | A | D | A | 理A 文C | A | 理A 文C |
13.4
14.![]()
![]()
15.![]()
16.![]()
17.解(I)![]()
![]() ……………………2ˊ
……………………2ˊ
又![]()
![]()
![]() ……………………4ˊ
……………………4ˊ
![]()
解得![]() …………………………………6ˊ
…………………………………6ˊ
(II)![]()
![]() ……………………………10ˊ
……………………………10ˊ
解得![]() ………………………………………12ˊ
………………………………………12ˊ
18.解:(I)![]()
又![]() 为等数列,故
为等数列,故![]() 故
故![]()
(Ⅱ)![]()
![]()
![]() ①
①
![]()
![]() ②
②
②-①得
![]()
![]()
![]()
![]()
![]()
![]()
![]()
由![]() 从而
从而![]()
![]()
![]()
![]()
![]()
![]()
所以![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
21.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]() 由
由![]()
![]()
又![]() 当
当![]() ,不符合题意
,不符合题意
当![]()
![]()
![]()
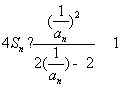
![]()
![]()
当![]()
整理得![]()
若对一切![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ……14分
……14分