2006年各地高考模拟创新试题之三——数列部分
1.把数列![]() 依次按第一个括号一个数,第二个括号两个数,第三个括号三个数,第四个括号四个数,第五个括号一个数,…循环分为(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39,41),(43)…则第104个括号内各数之和为
依次按第一个括号一个数,第二个括号两个数,第三个括号三个数,第四个括号四个数,第五个括号一个数,…循环分为(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39,41),(43)…则第104个括号内各数之和为
A.2036 B
2.数列![]() 满足
满足![]() 并且
并且![]() (
(![]() )。则数列的第100项为
)。则数列的第100项为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.在数列![]() 中,a1=2,
中,a1=2, ![]() ,则a5等于
,则a5等于
A.12 B
4.已知数列![]() 满足
满足![]() ,
,![]() ,若
,若![]() ,则
,则![]()
A.![]() B
B
5.已知数列![]() 中,
中,![]() 且对任意自然数n都有
且对任意自然数n都有![]() ,数列
,数列![]() 对任意自然数n都有
对任意自然数n都有![]()
(Ⅰ)求证数列![]() 是等比数列;
是等比数列;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)设数列![]() 前n项的和为Sn,求
前n项的和为Sn,求![]() 的值。
的值。
6.设函数![]() 在
在![]() 上为增函数.
上为增函数.
(Ⅰ)求正实数a的取值范围.
(Ⅱ)若![]() ,求证:
,求证:![]()
![]() ,
,![]() 且
且![]() .
.
7.定义如下运算:
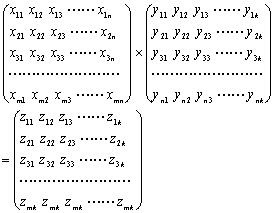
其中![]() ,
,![]() .
.
现有![]() 个正数的数表A排成行列如下:(这里用
个正数的数表A排成行列如下:(这里用![]() 表示位于第i行第j列的一个正数,
表示位于第i行第j列的一个正数,![]() ).
).

其中每横行的数成等差数列,每竖列的数成等比数列,且各个等比数列的公比相同,若![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求![]() 的表达式(用i,j表示);
的表达式(用i,j表示);
(Ⅱ)若 ,求
,求![]() .
.![]() ,用i,n表示) .
,用i,n表示) .
8.随着国家政策对节能环保型小排量车的调整,两款![]() 大致满足关系式:
大致满足关系式:![]() 0.
0.
(Ⅰ)求Q型车第n个月的月销售量![]() 的表达式;
的表达式;
(Ⅱ)求Q型车前n个月的销售总量![]() 的表达式;
的表达式;
(Ⅲ)比较两款车前n个月的销售总量![]() 与
与![]() 的大小关系.
的大小关系.
参考答案:
1.D
2.D
3.C
4.B
5.解:(Ⅰ)an+1 = ![]() ①
①
2an+2 = ![]() ②
②
②-①得2an+2-an+1 = ![]()
即bn+1 = ![]()
∴![]() 为常数
为常数
即{bn}为等比数列
(Ⅱ)an+1 = ![]()
![]()
= ![]()
= …
= ![]()
= 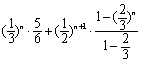
= ![]()
即{an}通项公式为
an = ![]()
(Ⅲ)an = ![]()
![]()
![]() = 3-1 = 2
= 3-1 = 2
6.解:(Ⅰ)由已知:![]()
依题意得:![]() 对
对![]() 恒成立,
恒成立,
∴![]() 对
对![]() 恒成立
恒成立
∴![]() 即:
即:![]() .
.
(Ⅱ)∵![]() ,∴由(Ⅰ)知:
,∴由(Ⅰ)知:![]() 在
在![]() 上为增函数,
上为增函数,
∴![]() 时
时 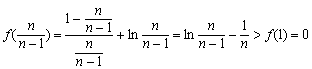
即 ![]() .
.
∴![]() .
.
设![]() ,
,![]() 则
则![]() 对
对![]() 恒成立,
恒成立,
∴![]() 在
在![]() 为减函数.
为减函数.
∴![]() 时
时 ![]() ,
,
即 ![]() ,
,
∴![]()
![]() .
.
综上所证::![]()
![]() ,
,![]() 且
且![]() 成立.
成立.
7.解:(Ⅰ)∵![]() ,
,![]() ,且每横行成等差数列,
,且每横行成等差数列,
∴ ![]() ,
,
∴ ![]() ,又∵
,又∵![]() ,∴
,∴![]() (∵
(∵![]() )
)
∴ ![]() ;
;
(Ⅱ)![]()
![]()
![]() ①
①
∴
![]() ②
②
②-①得
![]()
![]()
![]()
∴![]()
8.解:(Ⅰ)Q型车每月的销售量![]() 是以首项
是以首项![]() ,公比
,公比![]() 的等比数列,
的等比数列,![]() .
.
(Ⅱ)前n个月的销售总量![]() ,(
,(![]() ,且
,且![]() ).
).
(Ⅲ)![]()
![]()
![]() ,
,
又![]() ,
,![]() ,∴
,∴![]() .
.