2006年各地高考模拟创新试题之五——解析几何部分
1.设曲线C的方程为![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() 是曲线C的渐近线.根据以上定义可得曲线
是曲线C的渐近线.根据以上定义可得曲线![]() 的一条渐近线方程为 .
的一条渐近线方程为 .
2.设[x]表示不超过x的最大整数,又设x、y满足方程组![]() ,如果x不是整数,那么x + y是
,如果x不是整数,那么x + y是
A.在5与9之间 B.在9与11之间
C.在11与15之间 D.在15与16之间
3.已知向量![]() ,
,![]() ,
,![]() 与
与![]() 的夹角为60°,则直线
的夹角为60°,则直线![]() 与圆
与圆![]() 的位置关系是
的位置关系是
A.相切
B.相离 C.相交 D.随![]() 的值而定
的值而定
4.已知O平面上的一定点,A、B、C是平面上不共线的三个动点,点P满足![]()
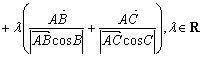 ,则动点P的轨迹一定通过△ABC的
,则动点P的轨迹一定通过△ABC的
A.重心 B.垂心 C.外心 D.内心
5.已知A、B、C是平面上不共线的三点,O为△ABC的外心,动点P满足![]()
![]() ,则P的轨迹一定通过△ABC的
,则P的轨迹一定通过△ABC的
A.内心 B.垂心 C.重心 D.AB边的中点
6.已知C为线段AB上一点,P为直线AB外一点,满足![]() ,
,![]() ,
,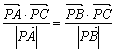 ,I为PC上一点,且
,I为PC上一点,且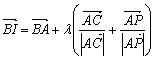
![]() ,则
,则![]() 的值为
的值为
A.1 B.2 C.![]() D.
D.![]()
7. 如果直线![]() 与圆
与圆![]() 交于M、N两点,且M、N关于直线
交于M、N两点,且M、N关于直线![]() 对称,动点
对称,动点![]() 在不等式组:
在不等式组: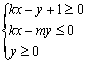 表示的平面区域内部及边界上运动,则
表示的平面区域内部及边界上运动,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若⊙C1:![]() 与⊙C2:
与⊙C2:![]() 在交点 处的切线互相垂直,则实数a的值为
.
在交点 处的切线互相垂直,则实数a的值为
.
9.过x轴上一点P向圆C:![]() 作切线,切点分别为A、B,则△PAB面积的最小值是
作切线,切点分别为A、B,则△PAB面积的最小值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.以椭圆![]() 的一个顶点C (0,1)为直角顶点作此椭圆的内接等腰直角三角形ABC,试问:这样的三角形是否存在?若存在,最多有几个?若不存在,说明理由.
的一个顶点C (0,1)为直角顶点作此椭圆的内接等腰直角三角形ABC,试问:这样的三角形是否存在?若存在,最多有几个?若不存在,说明理由.
11.已知椭圆![]() 两焦点分别为F1、F2,P是椭圆在第一象限弧上一点,并满足
两焦点分别为F1、F2,P是椭圆在第一象限弧上一点,并满足![]() ,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
(Ⅰ)求P点坐标;
(Ⅱ)求证直线AB的斜率为定值;
(Ⅲ)求△PAB面积的最大值.
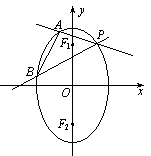
12.某校兴趣小组运用计算机对轮船由海上行驶入内陆海湾进行了一次模拟试验。如图,内陆海湾的入口处有暗礁,图中阴影所示的区域为暗礁区,其中线段AA1、B1B、CC1、D1D关于坐标轴或原点对称,线段B1B的方程为![]() ,过O有一条航道。有一艘正在海面上航行的轮船准备进入内陆海湾,在点
,过O有一条航道。有一艘正在海面上航行的轮船准备进入内陆海湾,在点![]() 处测得该船发出的汽笛声的时刻总晚
处测得该船发出的汽笛声的时刻总晚![]() (设海面上声速为
(设海面上声速为![]() )。若该船沿着当前的航线航行(不考虑轮船的体积)
)。若该船沿着当前的航线航行(不考虑轮船的体积)
(Ⅰ)问兴趣小组观察到轮船的当前的航线所在的曲线方程是什么?
(Ⅱ)这艘船能否由海上安全驶入内陆海湾?请说明理由。

参考答案:
1.解析:依题目提供的信息有:
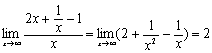 ,且
,且![]() ,由此可知曲线
,由此可知曲线![]() 的一条渐近线方程为
的一条渐近线方程为![]() .
.
2.D
3.B
4.C
5.D
6.C
7.D
8.![]()
9.A
10.解:设A、B两点分别居于y轴的左右两侧,
设CA的斜率为k,则![]() ,CA所在直线的方程为
,CA所在直线的方程为![]() ,代入椭圆的方程并整理
,代入椭圆的方程并整理
得![]() ,∴
,∴![]() 或
或![]() .
.
∴A点的横坐标为![]() .∴
.∴![]() .
.
同理, ![]() ,由
,由![]() 得
得![]() ,∴
,∴![]() ①
①
当![]() 时,
时,![]() ,
,![]() 无实数解;
无实数解;
当![]() 时,①的解是
时,①的解是![]() ,
,![]() 的解也是k=1;当
的解也是k=1;当![]() 时,①的解除
时,①的解除![]() 外,方程
外,方程![]() 有两个不等的正根,且都不等于1,故①有3个正根.
有两个不等的正根,且都不等于1,故①有3个正根.
∴符合题意的等腰直角三角形一定存在,最多有3个.
11.解:(Ⅰ)由题可得![]() ,
,![]() ,设
,设![]()
则![]() ,
,![]() ,
,
∴![]() ,∵点
,∵点![]() 在曲线上,则
在曲线上,则![]() ,∴
,∴![]() ,从而
,从而![]() ,得
,得![]() .则点P的坐标为
.则点P的坐标为![]() .
.
(Ⅱ)由题意知,两直线PA、PB的斜率必存在,设PB的斜率为![]() ,
,
则BP的直线方程为:![]() .由
.由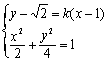 得
得![]()
![]() ,设
,设![]() ,则
,则![]() ,
,
同理可得![]() ,则
,则![]() ,
,![]() .
.
所以:AB的斜率![]() 为定值.
为定值.
(Ⅲ)设AB的直线方程:![]() .
.
由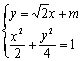 ,得
,得![]() ,
,
由![]() ,得
,得![]()
P到AB的距离为![]() ,
,
则![]()
![]() 。
。
当且仅当![]() 取等号
取等号
∴三角形PAB面积的最大值为![]() 。
。
12.解:设轮船所在的位置为P,由题意可得![]() 。
。![]() ,
,
故点P的轨迹是以M、N为焦点的双曲线的右支。
设点P的轨迹方程为![]()
![]() 则
则![]() ,
,![]() .
.
∴兴趣小组观察到轮船的当前航线所在的曲线方程是![]()
![]() .
.
(Ⅱ)这艘船能由海上安全驶入内陆海湾。
设直线![]() 的方程为
的方程为![]() 。
。
当![]() 时,设l与双曲线右支、直线
时,设l与双曲线右支、直线![]() 分别交于点Q1、S1,
分别交于点Q1、S1,
则 ![]() ,
,![]()
∵![]() .
.
∴点Q1在点S1的左侧,∴船不可能进入暗礁区.
当![]() 时,设l与双曲线右支、直线
时,设l与双曲线右支、直线![]() 分别交于点Q2、S2,
分别交于点Q2、S2,
则![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,∴Q2在点S2的右侧,∴船不可能进入暗礁区。
,∴Q2在点S2的右侧,∴船不可能进入暗礁区。
综上,在x轴上方,船不可能进入暗礁区,由对称性可知,船能由海上安全驶入内陆海湾。