湖北省黄石二中2004年高考模拟试卷(一)
数 学
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)
已知条件![]() ,条件
,条件![]() ,则
,则![]() 的
的
(A) 充分不必要条件 (B)必要不充分条件
(C) 既不充分也不必要条件 (D)充要条件
(2)
设![]() 表示两条直线,
表示两条直线,![]() 表示平面,给出下列四个命题
表示平面,给出下列四个命题
①若![]() ∥
∥![]()
②若![]() ∥
∥![]()
③若![]() ∥
∥![]()
④若![]() ∥
∥![]()
其中正确的命题个数是
(A) 1 (B) 2 (C)3 (D)4
(3)
若![]() ~
~![]() ,则下列说法正确的是
,则下列说法正确的是
(A) ![]() (B)
(B)
![]()
(C) 当![]() 时,若总体小于
时,若总体小于![]() 的取值为
的取值为![]() ,则
,则![]()
(D) 总体落在区间![]() 内的事件称为小概率事件.
内的事件称为小概率事件.
(4) 给出下列命题;
①若![]() 均为第一象限角,且
均为第一象限角,且![]() ,则
,则![]() ;
;
②若函数![]() 的最小正周期是
的最小正周期是![]() ,则
,则![]() ;
;
③函数![]() 是奇函数;
是奇函数;
④函数![]() 在
在![]() 上是增函数.
上是增函数.
其中正确命题个数是
(A) 0 (B) 1 (C) 2 (D)3
(5)
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为
(A) ![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(6)
椭圆![]() 的焦点在
的焦点在![]() 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的![]() 倍.则曲线
倍.则曲线![]() 的离心率为
的离心率为
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)![]()
(7)
设函数 ,
,![]() 的反函数为
的反函数为![]() .则
.则![]()
(A) ![]() (B)
1 (C)
(B)
1 (C)![]() (D)2
(D)2
(8) 如图所示为![]() 在
在![]() 上的图像,则它们所对应的图像编号顺序是
上的图像,则它们所对应的图像编号顺序是

(A) ①②③④ (B) ①③②④ (C) ③①②④ (D) ③①④②
(9)
(理科)设![]() 在
在![]() 上总是增函数,则实数
上总是增函数,则实数![]() 取值范围是
取值范围是
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)![]()
(文科)函数![]() 在区间
在区间![]() 上递减,且有最小值1,则
上递减,且有最小值1,则![]() 的值是
的值是
(A)2 (B)![]() (C)3 (D)
(C)3 (D)
![]()
(10)(理科)已知![]() ,
,![]() ,则
,则
(A) ![]() ≤
≤![]() ≤6 (B)
≤6 (B)
![]() ≤
≤![]() ≤8
≤8
(C) ![]() ≤
≤![]() ≤
≤![]() (D)
(D)
![]() ≤
≤![]() ≤7
≤7
(文科)若不等式![]() 成立的充分条件是
成立的充分条件是![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是
(A) ![]() ≥3 (B)
≥3 (B)
![]() ≥1 (C)
≥1 (C)![]() ≤1 (D)
≤1 (D)![]() ≤3
≤3
(11)等比数列![]() 中,
中,![]() ,
,![]() ,则
,则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(12)若函数![]() 没有最小值,则实数
没有最小值,则实数![]() 的取值范围是
的取值范围是
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() ≤1 (D)
≤1 (D)![]()
第Ⅱ卷(非选择题 共90分)
二. 填空题: 本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
(13)已知数列![]() 前
前![]() 项和为
项和为![]() ,则
,则![]() ____________________.
____________________.
(14)已知函数![]() 在R上连续,且
在R上连续,且![]()
![]() ,则
,则 ____________-.
____________-.
(15)(理)复数![]() 和
和![]() 满足
满足![]() ,若
,若![]() .则
.则![]() ______________.
______________.
(文)设![]() ,则
,则![]() __________________.
__________________.
(16) 今年某校有4位报考艺术专业的学生参加艺术类的考试,同时该校有4名老师参加监考. 考试中心有10个考室,若要求该校任何两名考生不在同一考室,4位老师每两位必须在同一考室,但不得监考本校学生,则安排方法共有__________种.(结果用数据回答)
三. 解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
一出租车司机从某饭店到火车站途中有六个交通岗,假设他在各交通岗遇到红灯这一事件是相互独立的,并且概率都是![]() .
.
(1) 求这位司机遇到红灯前,已经通过了两个交通岗的概率;
(2)
求这位司机遇到红灯数![]() 的期望与方差.
的期望与方差.
(18)(本小题满分12分)
已知向量![]() 且
且![]() .
.
(1)
求![]() ;
;
(2)
求函数![]() 的最值.
的最值.
(19)(本小题满分12分,以下两题选做一题,若甲,乙都做,只按甲题计分)
(甲)长方体![]() 中,
中,![]() 连接
连接![]() 过B作
过B作![]() 交
交![]() ,交
,交![]() 于F.
于F.
(1)
求证:![]() ;
;
(2)
求三棱锥![]() 的体积;
的体积;
(3)
求二面角![]() 的正切值.
的正切值.

(乙)直四棱柱![]() 的高为6,底面是边长为4,
的高为6,底面是边长为4,![]() 的菱形,
的菱形,![]() 相交于
相交于![]() 点,
点,![]() 与
与![]() 相交于
相交于![]() 点,点
点,点![]() 是
是![]() 的中点.
的中点.
(1)
求二面角![]() 的大小;
的大小;
(2)
分别以射线![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正半轴建立空间直角坐标系,求点
轴的正半轴建立空间直角坐标系,求点![]() 的坐标,并求异面直线
的坐标,并求异面直线![]() 所成角的大小.
所成角的大小.

(20)(本小题满分12分)
我国北方某城市严重缺水,曾一度取消全市的洗车行业.时间久了,车容影响了市容市貌.今年该市决定引进一种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车.污水净化器的价格是每台100万元,全市统一洗车价格10元.该市今年的汽车总量是101000辆,预计今后每年汽车数量将增加2000辆.洗车行A经过测算,如果全市的汽车总量是x,那么一年内在该洗车行洗车的平均辆次是![]() x,该洗车行每年的其他费用是1万元.问:洗车行A从今年开始至少经过多少年才能收回购买净化器的成本?
x,该洗车行每年的其他费用是1万元.问:洗车行A从今年开始至少经过多少年才能收回购买净化器的成本?
(21)(本小题满分12分)
已知![]() 为抛物线
为抛物线![]() 上任意一点,直线
上任意一点,直线![]() 为过点
为过点![]() 的切线,设直线
的切线,设直线![]() 交
交![]() 轴于点
轴于点![]() .
.![]() ,且
,且![]() .
.
(1)
当![]() 点运动时,求点
点运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)
求点![]() 到动直线
到动直线![]() 的最短距离,并求此时
的最短距离,并求此时![]() 的方程.
的方程.
(22)(本小题满分14分,文科学生做(1),(2),理科学生做(1),(2),(3))
已知函数![]() 与函数
与函数![]() 图像关于
图像关于![]() 对称.且函数
对称.且函数![]() ,(其中
,(其中![]() ,
,![]() 为常数)
为常数)
(1)
求函数![]() 的定义域;
的定义域;
(2)
问是否存在实数![]() ,使得
,使得![]() ,若存在,请求出
,若存在,请求出![]() ,若不存在,说明理由;
,若不存在,说明理由;
(3)
函数![]() 的定义域与值域能否同时为实数集
的定义域与值域能否同时为实数集![]() ?并证明你的结论.
?并证明你的结论.
数学答案
一 选择题
1.A 2.C 3.B 4.A 5.B 6.C 7.C 8.D 9.理D文D 10.理A文A 11.C 12.C
二 填空题
(13)61 (14)1 (15)理![]() 文
文![]() (16)18900
(16)18900
三 解答题
(17)(1)因为这位司机第一二个交通岗未遇到红灯,在第三个交通岗遇到红灯.所以![]()
(2)设司机遇到红灯次数为随机变量![]() ~
~![]()
![]()
![]() .
.
(18)(1)![]()
![]()
![]()
(2)![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
(19)甲
(1)由已知![]() ,又
,又![]()
∴![]() 又 ∵
又 ∵![]() ∴
∴![]()
![]()
![]()
∴![]()
∵ ![]()
∴
![]() 又 ∵
又 ∵![]()
![]()
由三垂线定理 ![]()
∵
![]()
∴
![]()
![]()
(2)在![]() 中,
中,![]() ~
~![]()
则![]()
故![]()
(3)由于![]()
![]() 在平面
在平面![]() 上的射影/
上的射影/
又 ![]()
![]()
![]() 又
又 ![]()
![]() 故
故 ![]() 故
故 ![]() .
.
乙
(1)
由已知过![]() 作
作![]() ,连接
,连接![]() ,由
,由![]()
![]() 故
故 ![]() 即为二面角
即为二面角![]() 的平面角.
的平面角.
易求 ![]()
(2)
由已知![]()
由![]()
设![]() 的夹角为
的夹角为![]()

故异面直线![]() 与
与![]() 所成角为
所成角为![]()
(20)设从今年开始至少经过![]() 年收回成本,
年收回成本,
![]() 年内的汽车数量构成以101000为首,2000为公差的等差数列,汽车数量总和为
年内的汽车数量构成以101000为首,2000为公差的等差数列,汽车数量总和为
![]()
![]() 年内的洗车收入为
年内的洗车收入为![]()
![]() )
)
依题意有
![]()
![]() )
)![]()
化简得 ![]()
解得 ![]() (年)
(年)
答:至少经过20年才能收回成本.
(21)设![]() 因为
因为![]() ,所以过点A的切线方程为
,所以过点A的切线方程为![]() .令
.令![]() ,B点坐标为(0,
,B点坐标为(0,![]()
又![]()
 消去
消去![]() ,得
,得![]()
(2)设C到![]() 的距离为
的距离为![]() ,则
,则
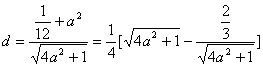
设![]() ,则
,则 的增函数
的增函数
![]()
故C到![]() 的最短距离为
的最短距离为![]() ,此时
,此时![]() 的方程为
的方程为![]() 。
。
(22)由已知![]() 关于
关于![]() 对称可知
对称可知
![]() 因此
因此 ![]()
(1)
若使![]() 有意义,则须使
有意义,则须使![]() ,由于
,由于![]()
![]()
当![]()
当![]()
综上,函数![]() 的定义域
的定义域
当![]() 时,
时, ![]()
当![]()
(2)由于![]() 的定义域关于直线
的定义域关于直线![]() 对称,且
对称,且![]() 的图像也关于直线
的图像也关于直线![]() 对称,∴
对称,∴![]() 的图像有对称轴
的图像有对称轴![]() ,且平行于
,且平行于![]() 轴, 即
轴, 即![]()
![]() .
.
(3)
当![]() 的定义域为
的定义域为![]() 时,由(1)知须有
时,由(1)知须有![]()
当![]() 的值域为
的值域为![]() 时,只要
时,只要![]() 的值域
的值域![]()
![]()
![]()
即须有使![]() ≥0,但此时
≥0,但此时![]() ≤1矛盾
≤1矛盾
∴函数![]() 的定义域的值域不能同时为
的定义域的值域不能同时为![]() 。
。