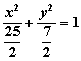2006年天利38套高考模拟卷汇编精华B
一、选择题:
1.下列命题中,使命题M是命题N成立的充要条件的一组命题是
A.M:a>b N:ac2>bc2
B.M:a>b,c>d N:a-d>b-c
C.M:a>b>0,c>d>0 N:ac>bd
D.M:a-b=a+b N:ab≤0
2. 如果![]() 的方差为3,那么2
的方差为3,那么2![]() 、2
、2![]() 、2
、2![]() 、
、
2![]() 、2
、2![]() 、2
、2![]() 的方差是 ( )
的方差是 ( )
A.0 B.3 C.6 D.12
3. 已知![]() 、
、![]() 是抛物线
是抛物线![]() (
(![]() >0)上异于原点
>0)上异于原点![]() 的两点,则“
的两点,则“![]() ·
·![]() =0”
=0”
是“直线![]() 恒过定点(
恒过定点(![]() )”的………………………………………………( B
)
)”的………………………………………………( B
)
A)充分非必要条件 B)充要条件
C)必要非充分条件 D)非充分非必要条
4.地球表面上从A地(北纬45°,东经120°)到B地(北纬45°,东经30°)的最短距离为(地球半径为R)( )
A.R B.![]() C.
C.![]() D.
D.![]()
5.(文)设F1、F2为椭圆![]() +y2=1的两焦点,P在椭圆上,当△F1PF2面积为1时,
+y2=1的两焦点,P在椭圆上,当△F1PF2面积为1时,![]() 的值为 ( )
的值为 ( )
A.0 B.1 C.2 D.![]()
(理)△ABC边上的高线为AD,BD=a,CD=b,且a<b,将△ABC沿AD折成大小为![]() 的二面角B—AD—C.若cos
的二面角B—AD—C.若cos![]() =
=![]() ,则三棱锥A—BDC的侧面△ABC是
,则三棱锥A—BDC的侧面△ABC是
A.锐角三角形
B.钝角三角形
C.直角三角形
D.形状与a、b的值有关的三角形
6. 已知F1、F2是椭圆![]() =1(5<a<10)的两个焦点,B是短轴的一个端点,则△F1BF2的面积的最大值是
=1(5<a<10)的两个焦点,B是短轴的一个端点,则△F1BF2的面积的最大值是
A.![]() B.
B.![]() C.100(3-2
C.100(3-2![]() ) D.
) D.![]() a2
a2
7、已知向量![]() ,其中
,其中![]() 、
、![]() 均为非零向量,则
均为非零向量,则![]() 的取值范围是
的取值范围是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8 、函数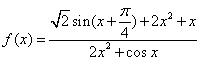 的最大值为M,最小值为N,则M+N=
的最大值为M,最小值为N,则M+N=
A、2 B、3 C、 4 D、5
9、甲、乙两人约定在6时到7时之间在某处会面,并且约定先到者应等候另一个人15分钟,过时即不再等了,则两人能会上面的概率为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、已知定义域为实数集上的函数![]() 满足
满足![]() ,且
,且![]() 不恒为零,则
不恒为零,则![]() 是
是
A 、奇函数 B、偶函数 C 、非奇非偶函数 D、不能确定
11、设函数![]() ,
,![]() ,
,![]() 是函数
是函数![]() 的单调递增区间,将
的单调递增区间,将![]() 的图象按
的图象按![]() 平移得到一个新的函数
平移得到一个新的函数![]() 的图象,则
的图象,则![]() 的单调递增区间必定是
的单调递增区间必定是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、假设每一架飞机的引擎在飞行中出现故障率为1-p,且各引擎是否有故障是独立的,如有至少50%的引擎能正常运行,飞机就可成功飞行。若使4引擎飞机比2引擎飞机更为安全,则p的取值范围是
A、(![]() )
B、(
)
B、(![]() ) C、(
) C、(![]() ) D、(
) D、(![]() )
)
13、对一切实数![]() ,不等式
,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是
A、![]() B、
B、![]() C、
C、![]() D
D ![]()
14、已知![]() 是异面直线,有下面四个结论:
是异面直线,有下面四个结论:
⑴
必存在平面![]() 过
过![]() 且与
且与![]() 平行;⑵ 必存在平面
平行;⑵ 必存在平面![]() 过
过![]() 且与
且与![]() 垂直;
垂直;
⑶ 必存在平面![]() 与
与![]() 都垂直; ⑷ 必存在平面
都垂直; ⑷ 必存在平面![]() 与
与![]() 距离都相等。
距离都相等。
A、⑴⑵ B、⑴⑷ C、⑴⑶ D ⑵⑶
15、已知A、B、C是表面积为48![]() 的球面上三点,AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成的角是
的球面上三点,AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成的角是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
16、已知数列![]() 满足
满足![]() ,
,![]()
![]() ,则当
,则当![]() 时,
时,![]() 为
为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
17、方程![]() =
=![]() 的实根个数是
的实根个数是
A、3 B、2 C、1 D、0
18、同时具有性质“⑴ 最小正周期是![]() ;⑵ 图象关于直线
;⑵ 图象关于直线![]() 对称;⑶ 在
对称;⑶ 在![]() 上是增函数”的一个函数是
上是增函数”的一个函数是
A、![]() B、
B、![]()
C、![]() D、
D、![]()
19、函数f(x)在x=0处无意义,对于所有的非零实数x都成立![]() ,
,
则适合方程![]() 的
的![]() 值的个数
值的个数
A、恰好只有一个 B、恰好有两个
C、为0个 D、为无穷多个,但不是所有的非零实数
20、若函数f(x)=log2(x+1)且a>b>c>0,则![]() 、
、![]() 、
、![]() 的大小关系是
的大小关系是
A、![]() >
>![]() >
>![]() B、
B、![]() >
>![]() >
>![]()
C、![]() >
>![]() >
>![]() D、
D、![]() >
>![]() >
>![]()
二、填空题:
21、某公司生产三种型号的轿车,产量分别为1200辆,6000辆和2000辆,为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车依次应抽取______,_______,_______辆.
22、某班有50名同学,现报名参加两项比赛,参加A项的有30人,参加B项的有33人,且A、B两项都不参加的同学人数比A、B两项都参加的同学人数的三分之一多一人,则仅参加B项的人数为_________________
23、若关于![]() 的方程
的方程![]() 的两根分别在区间
的两根分别在区间![]() 与
与![]() 内,则
内,则![]() 的取值范围是
。
的取值范围是
。
24、经过△OAB的重心G的直线与OA、OB两边分别交于P、Q,设![]() ,
,![]() 向量,则m+n=
。(写出m、n的关系式)
向量,则m+n=
。(写出m、n的关系式)
25、设函数![]() ,给出下列4个命题:
,给出下列4个命题:
①![]() 时,
时,![]() 只有一个实数根; ②
只有一个实数根; ②![]() 时,
时,![]() 是奇函数;
是奇函数;
③![]() 的图象关于点
的图象关于点![]() 对称;
④方程
对称;
④方程![]() 至多有2个实数根
至多有2个实数根
上述命题中的所有正确命题的序号是 .
26、对于正整数![]() 和
和![]() ,定义
,定义![]() !=
!=![]() ,其中
,其中![]() ,且
,且![]() 是满足
是满足![]() 的最大整数,则(
的最大整数,则(![]() !)/(10
!)/(10![]() !)=___________
!)=___________
27、关于![]() 的方程
的方程![]() 在区间
在区间![]() ]上有两个相异实根
]上有两个相异实根![]() ,则实数
,则实数![]() 的取值范围是___________________
的取值范围是___________________
28、已知![]() (
(![]() 为锐角),那么
为锐角),那么![]() 的最大值为________________________
的最大值为________________________
29、若平移椭圆![]() ,使平移后的椭圆的中心在第一象限,且它与
,使平移后的椭圆的中心在第一象限,且它与![]() 轴、
轴、![]() 轴分别只有一个交点,则平移后的椭圆方程是____________________
轴分别只有一个交点,则平移后的椭圆方程是____________________
三、解答题:
30、已知向量![]() ,ω>0,记函数
,ω>0,记函数![]() =
=![]() ,已知
,已知![]() 的最小正周期为
的最小正周期为![]() .
.
⑴ 求ω的值;
⑵ 设△ABC的三边a、b、c满足b2=ac,且边b所对的角为![]() ,
,
求此时函数![]() 的值域。
的值域。
31、阅读下列文字,然后回答问题:
对于任意实数![]() ,符号[
,符号[![]() ]表示
]表示![]() 的整数部分,即[
的整数部分,即[![]() ]是不超过
]是不超过![]() 的最大整数”.在实数轴R(箭头向右)上[
的最大整数”.在实数轴R(箭头向右)上[![]() ]是在点
]是在点![]() 左侧的第一个整数点,当
左侧的第一个整数点,当![]() 是整数时,[
是整数时,[![]() ]就是
]就是![]() .这个函数[
.这个函数[![]() ]叫做“取整函数”,也叫做高斯(Gauss)函数,它在数学本身和生产实践中有广泛的应用.例如当您在学习和使用计算器时,在用到的算法语言中,就有这种取整函数.
]叫做“取整函数”,也叫做高斯(Gauss)函数,它在数学本身和生产实践中有广泛的应用.例如当您在学习和使用计算器时,在用到的算法语言中,就有这种取整函数.
试求![]() 的和.
的和.
32、(本小题满分12分)
设事件A发生的概率为P,若在A发生的条件下B发生的概率为P/,则由A产生B的概率为PP/,根据这一规律解答下题:一种掷硬币走跳棋的游戏:棋盘上有第0,1,2,3,…,100,共101站,设棋子跳到第![]() 站的概率为
站的概率为![]() ,一枚棋子开始在第0站(即
,一枚棋子开始在第0站(即![]() ),由棋手每掷一次硬币,棋子向前跳动一次,若硬币出现正面则棋子向前跳动一站,出现反面则向前跳动两站,直到棋子跳到第99站(获胜)或100站(失败)时,游戏结束。已知硬币出现正反面的概率都为
),由棋手每掷一次硬币,棋子向前跳动一次,若硬币出现正面则棋子向前跳动一站,出现反面则向前跳动两站,直到棋子跳到第99站(获胜)或100站(失败)时,游戏结束。已知硬币出现正反面的概率都为![]() 。
。
⑴ 求![]() ,并根据棋子跳到第
,并根据棋子跳到第![]() 站的情况,试用
站的情况,试用![]() 表示
表示![]() ;
;
⑵ 设![]() ,求证:数列
,求证:数列![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
⑶ 求玩该游戏获胜的概率
33、(本小题满分12分)
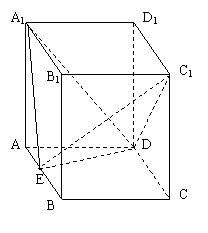 如图:直平行六面体ABCD-A1B1C1D1,底面ABCD是边长为2a的菱形,∠BAD=600,E为AB中点,二面角A1-ED-A为600
如图:直平行六面体ABCD-A1B1C1D1,底面ABCD是边长为2a的菱形,∠BAD=600,E为AB中点,二面角A1-ED-A为600
(I)求证:平面A1ED⊥平面ABB1A1;
(II)求二面角A1-ED-C1的余弦值;
(III)求点C1到平面A1ED的距离。
34、(本小题满分14分)
椭圆E的中心在原点O,焦点在x轴上,离心率![]() ,过点C(-1,0)的直线l交椭圆于A、B两点,且满足:
,过点C(-1,0)的直线l交椭圆于A、B两点,且满足:![]() (λ≥2)。
(λ≥2)。
(1)若λ为常数,试用直线l的斜率k(k≠0)表示三角形OAB的面积;
(2)若λ为常数,当三角形OAB的面积取得最大值时,求椭圆E的方程;
(3)若λ变化,且λ=k2+1,试问:实数λ和直线l的斜率k(k∈R)分别为何值时,椭圆E的短半轴长取得最大值?并求出此时的椭圆方程。
35、已知函数![]()
![]()
(1)若![]() 且函数
且函数![]() 的值域为
的值域为![]() ,求
,求![]() 的表达式;
的表达式;
(2)在(1)的条件下,
当![]() 时,
时, ![]() 是单调函数, 求实数k的取值范围;
是单调函数, 求实数k的取值范围;
(3)设![]() ,
, ![]()
![]() 且
且![]() 为偶函数, 判断
为偶函数, 判断![]() +
+![]() 能否大于零?
能否大于零?
36、已知:f(x)=![]() (x<-2),f(x)的反函数为g(x),点An(an,
(x<-2),f(x)的反函数为g(x),点An(an,![]() )在曲线y=g(x)上(n∈
)在曲线y=g(x)上(n∈![]() ),且a1=1.
),且a1=1.
(I)求y=g(x)的表达式;
(II)证明数列{![]() }为等差数列;
}为等差数列;
(Ⅲ)求数列{an}的通项公式;
(Ⅳ)设bn=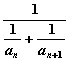 ,记Sn=b1+b2+……+bn,求Sn.
,记Sn=b1+b2+……+bn,求Sn.
37、已知动圆与圆F1:x2+y2+6x+4=0和圆F2:x2+y2-6x-36=0都外切。
(I)求动圆圆心的轨迹C的方程;
(II)若直线l被轨迹C所截得的线段的中点坐标为(-20,-16),求直线l的方程;
(Ⅲ)若点P在直线l上,且过点P的椭圆C∕以轨迹C的焦点为焦点,试求点P在什么位置时,椭圆C∕的长轴最短,并求出这个具有最短长轴的椭圆C∕的方程。
参考答案
一、选择题:1-5,DDBCA; 6-10,BCADA; 11-15,DCBBD 16-20,CCCBB
二、填空题:21、6,30,10; 22、12人; 23、![]() ; 24、3mn; 25、1,2,3;
; 24、3mn; 25、1,2,3;
26、![]() ; 27、
; 27、![]() ; 28、
; 28、![]() ; 29、
; 29、![]() ;
;
三、解答题:
30、解:(1)∵![]()
∴f(x)=![]() =
=![]() =
=![]()
=![]() =
=![]() (4分)
(4分)
∴周期T=![]() =
=![]() ∴ω=2(6分)
∴ω=2(6分)
(2)由(1)知:![]() (7分)
(7分)
∵b2=ac,∴在△ABC中由余弦定理得:
![]() ≥
≥![]() (9分)
(9分)
又因为余弦函数在[0,π]上是减函数,∴![]() (10分)
(10分)
且![]() (10分)∴
(10分)∴![]()
∴![]() (11分)
(11分)
即:函数f(x)的值域为[![]() ].(12分)
].(12分)
31、解:![]()
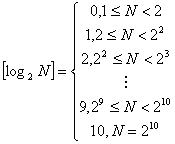 (6分)
(6分)
故原式=![]()
=![]() . (12分)
. (12分)
32、解:(1)![]() ,
,![]()
![]() (5分)
(5分)
![]() (7分)
(7分)
(2) 依题意:![]()
∴ ![]()
∴![]() 表示等比数列 (9分
表示等比数列 (9分
又![]()
![]() (11分)
(11分)
答:(1);(2) (12分)
33、(I) 证明:连结BD,在菱形ABCD中,∠BAD=600,
∴△ABD为正三角形,
∵E为AB的中点,∴ED⊥AB (1分)
在直六面体ABCD-A1B1C1D1中:平面ABB1A1⊥平面ABCD且交于AB,
∵ED![]() 面ABCD∴ED⊥面ABB1A1 (2分)
面ABCD∴ED⊥面ABB1A1 (2分)
∴平面A1ED⊥平面ABB1A1 (3分)
(II)解: 由(I)知:ED⊥面ABB1A1
∵A1E![]() 面ABB1A1 ∴A1E⊥ED
面ABB1A1 ∴A1E⊥ED
又在直平行六面体ABCD-A1B1C1D1中:AA1⊥面ABCD,
由三垂线定理的逆定理知:AE⊥ED,∴∠A1EA=600 (4分)
取BB1的中点F,连EF、AB1,则EF![]()
![]() ,
,
在直平行六面体ABCD-A1B1C1D1中:AB1![]() DC1∴EF
DC1∴EF![]()
![]()
∴E、F、C1、D四点共面(5分)
∵ED⊥面ABB1A1且EF![]() 面ABB1A1
面ABB1A1
∴EF⊥ED ∴∠A1EF为二面角A1-ED-C1的平面角(6分)
在Rt△EBF中:![]() ,
,![]()
在Rt△A1AE中:![]() ,
,
在Rt△A1B1F中:![]() (7分)
(7分)
∴在Rt△A1EF中: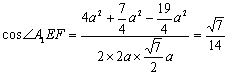
∴二面角A1-ED-C1的余弦值为![]() (8分)
(8分)
(III)过F作FG⊥A1E交A1E于G点
∵平面A1ED⊥面ABB1A1 且平面A1ED∩面ABB1A1=A1E
∴FG⊥平面A1ED,即:FG是点F到平面A1ED的距离(10分)
在Rt△EGF中:![]()
∴![]() ∴
∴![]() (11分)
(11分)
∵EF![]()
![]() 且E、D∈面A1ED
且E、D∈面A1ED
∴点C1到平面A1ED的距离为![]() (12分)
(12分)
34、设椭圆方程为:![]() (a>b> 0),由
(a>b> 0),由![]() 及a2=b2+c2得a2=3b2,故椭圆方程为x2+3y2=3b2①
及a2=b2+c2得a2=3b2,故椭圆方程为x2+3y2=3b2①
(1)∵直线L:y=k(x+1)交椭圆于A(x1,y1),B(x2,y2)两点,
并且![]() (λ≥2)
(λ≥2)
∴(x1+1,y1)=λ(-1-x2,-y2),即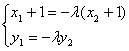 ②把y=k(x+1)代入椭圆方程,得:(3k2+1)x2+6k2x+3k2-3b2=0,且△=k2(3b2-1)+b2>0,
②把y=k(x+1)代入椭圆方程,得:(3k2+1)x2+6k2x+3k2-3b2=0,且△=k2(3b2-1)+b2>0,
∴![]() ③
③![]() ④
④
∴![]() 联立②、③得:
联立②、③得:![]() ∴
∴![]() (6分)
(6分)
(2)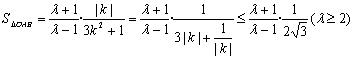 当且仅当
当且仅当![]()
即![]() 时,S△OAB取得最大值。此时
时,S△OAB取得最大值。此时![]() ,又∵x1+1=-λ(x2+1),
,又∵x1+1=-λ(x2+1),
∴![]() ,代入④得:
,代入④得:![]()
故此时椭圆的方程为 ![]() (10分)
(10分)
(3)由②、③联立得:![]()
![]()
将x1、x2代入④得:![]() 由k2=λ-1
由k2=λ-1
得:![]()
易知:当λ≥2时,3b2是λ的减函数,故当λ=2时,(3b2)max=3.故当λ=2,
k=±1时,椭圆短半轴长取得最大值,此时椭圆方程为x2+3y2=3。(14分)
35、(1) ∵![]() , ∴
, ∴![]()
又![]() 恒成立,
恒成立,
∴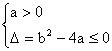 , ∴
, ∴![]() ,
, ![]() ……2分
……2分
∴![]() . ∴
. ∴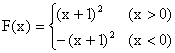 ……4分
……4分
(2)![]()
![]() , 当
, 当![]() 或
或![]() 时,
时,
即![]() 或
或![]() 时,
时, ![]() 是单调函数……………………8分
是单调函数……………………8分
(3) ∵![]() 是偶函数
是偶函数
∴![]()
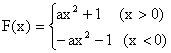 ,
,
∵![]() 设
设![]() 则
则![]() .
.
又![]() ∴
∴![]() ……………………10分
……………………10分
![]() +
+![]()
![]() ,
,
∴![]() +
+![]() 能大于零. ……………………14分
能大于零. ……………………14分
36、(Ⅰ)由y=![]() 得
得![]() ,∴
,∴![]()
∵x<—2,∴![]() ,∴g(x)=
,∴g(x)= ![]() (x>0)
(x>0)
(II)∵点An(an,![]() )在曲线y=g(x)上(n∈N+),∴
)在曲线y=g(x)上(n∈N+),∴![]() =g(an)=
=g(an)=![]() ,并且an>0
,并且an>0
![]() ,
,![]() ,∴数列{
,∴数列{![]() }为等差数列。
}为等差数列。
(III)∵数列{![]() }为等差数列,并且首项为
}为等差数列,并且首项为![]() =1,公差为4,
=1,公差为4,
∴![]() =1+4(n—1),∴
=1+4(n—1),∴![]() ,∵an>0,∴
,∵an>0,∴![]() ,
,
(Ⅳ)bn=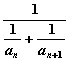 =
=![]() ,
,
∴Sn=b1+b2+…+bn=![]() =
=![]()
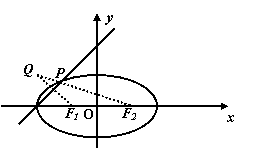 37、.解:(I)圆F1:(x+3)2+y2=5 , 圆F2:(x-3)2+ y2=45
37、.解:(I)圆F1:(x+3)2+y2=5 , 圆F2:(x-3)2+ y2=45
设动圆半径为r,圆心为M,则由已知得:
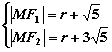 ,∴MF2-MF1=2
,∴MF2-MF1=2![]()
∴动圆圆心的轨迹C为以F1,F2为焦点,实轴长为2![]() 的双曲线的左支,
的双曲线的左支,
易得其方程为:![]() (x<0)
(x<0)
(Ⅱ)设l方程为:y+16=k(x+20),并设l与轨迹C交点坐标为(x1,y1),(x2,y2),则由已知得:![]() , 即x1+x2=-40……①
, 即x1+x2=-40……①
由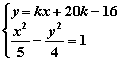 消去y得:
消去y得:
(4-5k2)x2-10k(20k-16)x-5(20k-16)2-20=0
∴x1+x2=![]() ……②
……②
由①、②得:![]() =-40,∴k=1
=-40,∴k=1
∴所求直线l的方程为y=x+4
(Ⅲ)椭圆的长轴长等于PF1+PF2,要长轴最短,只需在直线l上找一点P,使点P到F1、F2的距离之和最小。
由平面几何知识知:作F1关于l的对称点Q,连结QF2交直线l于点P,则点P即为所求点,坐标为(![]() )
)
此时长轴2a=PF1+PF2=PQ+PF2=QF2=5![]() 从而a2=
从而a2=![]() ,c=3
,c=3
∴b2=a2—c2=![]()
∴椭圆C′的方程为: