宣威六中2005年高考第一轮总复习同步试卷（十六）（期中卷）
（集合、函数、数列、三角函数）出题人：符佐玺
考试时间：2004年11月23日
一、选择题（5×12=60）
1．已知集合M={0，x}，N={1，2}，若M∩N={1}，则M∪N为 ( )
A．｛0,x,1,2｝ B．{1,2,0,1} C．{0,1,2} D．不能确定
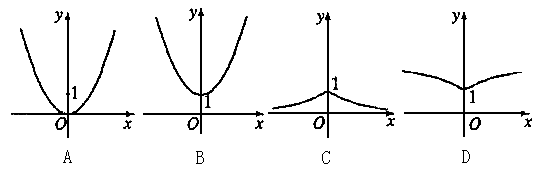
4. 成等差数列的3个正数的和等于15，并且这三个数分别加上1，3，9后又成等比数列。那么这三个数的乘积等于（ ）
A. 210 B. 105 C. 70 D. 35
5. 把函数y=f(2x)的图象变成函数y=f(2x+4)的图象，要经过的变换为（ ）
A. 把图象向左平移2个单位 B. 把图象向右平移2个单位
C. 把图象向左平移4个单位 D. 把图象向右平移4个单位
7. 已知集合A={1，2，3}，B={4，5，6}，映射f：A→B，且满足1的象是4，则这样的映射共有（ ）
A. 2个 B. 4个 C. 6个 D. 9个
8．“
”的含义是( )
A．
不全为0
B． 全不为0
C．至少有一个为0 D．
不为0且
为0，或不为0且为0
9．已知等差数列
的通项公式为
其前n项和为Sn，则数列
的前10项的和为（ ）
A．120 B．70 C．75 D．100
10．函数
的最小正周期是(
)
A．
B．2π
C．π
D．
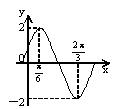
11. 函数y＝Asin(ωx＋φ)
的图象如图所示，则y的表达式为( )
A.y＝2sin(
) B.y＝2sin(
)
C.y＝2sin(2x＋
) D.y＝2sin(2x－)
12 设
的值为（ ）
A、1 B、－1 C、－
D、
二、填空题（4×4＝16）
13、（文）如果扇形的半径为
，面积为
，那么这个扇形的圆心角的弧度数为________。（理）
14．（文）黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：
则第n个图案中有白色地面砖____________块.
（理）已知
，把数列
的各项排成三角形状；记A（m,n）表示第m行，第n列的项，则
A（10，8）= .
15、函数
的单调递减区间是________________________。
16．若不等式
对一切实数x恒成立,则实数a的取值范围是
三、解答题（17－21每题12分，22题14分）
17 （理科）
（文科）
18
19．（本小题满分12分）已知函数f(x)=sin(wx+j)，xÎR，(其中w>0)的图象与x轴在原点右侧的第一个交点为N（6,0）,又f(2+x)=f(2－x),f(0)<0,求这个函数的解析式.
20.(本小题满分12分) 已知、
，函数
，若函数的值域为[－5,1]，求常数、的值.
21 已知函数f(x)=2
－1的反函数为f-1(x)，g(x)=log
(3x+1).
(1)若f-1(x)≤ g(x)，求x的取值范围D;
(2)设函数H(x)= g(x)－ f－1(x)，当x∈D时,求函数H(x)的值域.
22 已知数列中，a1=1，前n项和为Sn，对于任意的
总成等差数列.
（Ⅰ）求
的值；
（Ⅱ）求数列的通项an;
（Ⅲ）证明
宣威六中2005年高考第一轮总复习同步试卷（十六）（期中卷）
参考答案
一、选择题（5×12=60）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | C | C | B | A | B | D | A | C | C | C | D |
二、填空题（4×4＝16）
13、（文）
(理）
14.（文）
（理）2·
15 (2,+∞) 16.
三解答题（17－21每题12分，22题14分）
17 解： 
（理科评分）
（文科评分）
18 解：
19. 解：
f(2+x)=f(2-x)
f(x)关于x=2对称，又x轴在原点右侧的第一个交点为N（6,0）
=6-2=4，即T=16，
=
。
……4分
将N（6,0）代入f(x)=sin(x+j)得：sin(
+j)=0，
得：j=2k
+
或j=2k+
(kÎZ),
……8分
f(0)<0, j=2k+(kÎZ),满足条件的最小正数j=, ……10分
所求解析式f(x)=sin(x+)。
……12分
20解：
…………3分
…………6分
当
时，
………………8分
当
时，
……………10分
当
时，不合题意.………………………………………………………11分
综上所述，
或
……………………………………12分
21．解：（1）由
--2分
若
即x的范围D=[0，1]……………………6分
（2）
令
.
有
………………………………12分
22．解：（Ⅰ）
……4 分
（Ⅱ）
①（
②
②—①:
10 分
（Ⅲ）
