重庆市重点中学高2006级高考最后演练试卷
数 学（文科）
第Ⅰ卷(选择题 共60分)
参考公式：
如果事件A、B互斥，那么 球的表面积公式
P(A+B)=P(A)+P(B)
如果事件A、B相互独立，那么 其中R表示球的半径
P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是 球的体积公式
P，那么n次独立重复试验中恰好发生k
次的概率
其中R表示球的半径
第Ⅰ卷（选择题共60分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1、设
是集合A到B的映射，如果B＝｛1，2｝，则
只可能是
A. 
或｛1｝ B.
｛1｝ C. 或｛2｝ D.
或｛1｝或｛2｝
2、条件
，条件
，则
是
的
A．充分非必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要的条件
3、
的最小正周期为
A.
B.
C.
D.
4、曲线y=x3在点P处的切线斜率为k，当k=3时的P点坐标为
A.(－2,－8)
B.(－1,－1),(1,1) C.(2,8) D.(－1
,－1 )
5、若
，则
A．2003 B．0 C．2004 D．2006
6、向量
，
，则向量
与向量
的夹角的范围是
A．
B．
C．
D．
7、已知函数
，且满足
，
，则
的取值范围是
A．
B．
C．
D．
8、函数
与
,(其中
且
)的图象关于
A．直线
对称
B．直线
对称
C．直线
对称
D．直线
对称
9、设集合A=
,若点P（2，3）
，则m+n的最小值是
A．-6 B．
10、如图，正方体ABCD－A1B
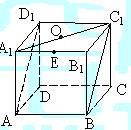A．
B．
C．
D． 
11、已知集合A={a,b,c,d,e},B={1,2,3,4,5},则从A到B的所有函数中，
存在反函数的概率为
A．
B．
C．
D． 
12、已知
是定义在R上的函数，且
，若
，则
的值为
A．
B．
C．
D．
第II卷（非选择题共90分）
二、填空题：(本大题共4小题，每小题4分，共16分。把答案填在答题卷中相应位置上。)
13、已知
,sinθ=a,(0≤θ≤
)，则cotθ=
14、可行域
内的所有的点中,横坐标与纵坐标均为整数的整点共有
个．
15、已知函数
，则不等式
的解集是
16、定义一种运算“*”，对于正整数n满足以下运算性质：（1）1*1=2，（2）(n+1)*1=2(n*1)，则n*1用含n的代数式表示是
三.解答题(本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤)
17、（本题满分13分）已知
，
。
（1）求y关于x的函数关系式
（2）若
时，的最大值为4，求a的值，并说明此时的图象的对称轴方程及对称中心的坐标。
18、（本题满分13分）从10个元件中（其中4个相同的甲品牌元件和6个相同的乙品牌元件）随机选出3个参加某种性能测试. 每个甲品牌元件能通过测试的概率均为
，每个乙品牌元件能通过测试的概率均为
.试求：
（1）选出的3个元件中，至少有一个甲品牌元件的概率；
（2）若选出的三个元件均为乙品牌元件，现对它们进行性能测试，求至少有两个乙品牌元件同时通过测试的概率.
19、（本题满分12分）已知函数
在
时有极大值
（1）求
的解析式并求出单调区间；
（2）解不等式
。
20、（本题满分12分）如图，P—ABCD是正四棱锥,
是正方体，其中
.
（1）求证：
；
（2）求平面PAD与平面
所成的锐二面角
的大小；
21、（本题满分12分）在
中，两个定点
，的垂心H（三角形三条高线的交点）是AB边上高线CD的中点。
（1）求动点C的轨迹方程；
（2）斜率为2的直线l交动点C的轨迹于P、Q两点，求
面积的最大值（O是坐标原点）。
22、（本题满分12分）
已知在（－1，1）上有定义，
=1，且满足
对数列
（1）证明：在（－1，1）上为奇函数；
（2）求
的表达式；
（3）是否存在自然数m，使得对于任意
成立？若存在，求出m的最小值.
重庆市重点中学高2006级高考最后演练试卷
数学参考答案（文科）
一、 选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1、A 解析:A等于{1}或{-1} 或{
} 或{- }或这些集合的并集。
2、A 解析: 由
得
或
, 则为
,又由得为
, ∵
, ∴是的充分非必要条件 ,故选A
3、C
解析:
，∴最小正周期为，故选C。
4、B
解析：由y=x3，得y′=3x2.由已知得3x2=3，x=±1.
当x=1时，y=1,当x=－1时，y=－1，
故P点的坐标为(1，1)或(－1，－1)，故选B.
5、A 解析:
令
得 , 得
, 令
, 得
,
. 故选A
|
|
6、B 解析:由题意点A坐标（2，0），
点B是圆
上的动点，
由图形知与向量的夹角的范围是．故选B
7、A 解析:∵
，
∴
，
∵
．又
，
，
∴
．∴的取值范围是．故选A
8、C 解析: ∵函数
与
的图象关于直线对称 ,而函数与的图象分别是由函数与的图象向左平移1个单位而得,
∴函数与的图象的对称轴可以是由直线向左平移1个单位可得对称轴为 故选C .
9、C
解析:由点P（2，3），得
即
；
，即
故选C。
10、B 解析：因为在正方体ABCD-A1B1C1D1中，A1B1平行于平面ABC1D1。
所以点E到平面ABC1D1距离转化为点B1到平面AB C1D1距离，即
故选B。
11、 D
解析:从A到B的所有函数共有55=3125个，而从A到B的所有反函数共有
个， 故存在反函数的概率为
12、A． 解析：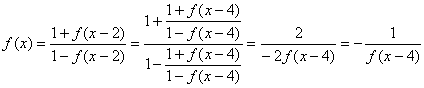
，即函数的周期为8，
故=f(6)=
故选A。
二、填空题：(本大题共4小题，每小题4分，共16分。把答案填在答题卷中相应位置上。)
13、
解析: 
,
sinθ=a=
，0≤θ≤则cotθ=
14、12 解析:作出可行域如图所示, 可得共有12个整点.。
15、[-2，2]
解析:`当
时
；
当
时
故不等式的解集是[-2，2]
16、2n 解析:由（2）（2）可得2*1=2（1*1）=22，3*1=2（2*1）=23，……n*1=2n
三.解答题(本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤)
17、解：（1）
因为，
所以
（2）因为时，的最大值为4，
所以
故
所以函数
即
时函数有最大值或最小值；
故函数的图象的对称轴方程为
时函数值为2，
故函数的对称中心的坐标为
。
18、解：（1）随机选出的3个元件中，至少有一个甲品牌元件的概率为
1－
；………………6分
（2）至少有两个乙品牌元件同时通过测试的概率为
=
；………………12分
19、解：
（1）
，
函数在时有极大值
即
即
故
此时
令
得
| x |
| -1 |
|
|
|
|
| + | 0 | - | 0 | + |
|
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
故的增区间是
，
减区间是
（2），
不等式即为
即为
故
，原不等式的解集为{xx>0,或x<-1}
20、解法一:
(1) 连结AC , 交BD于点O , 连结PO ,
则PO⊥面ABCD
, 又∵AC⊥BD , ∴
,
∵BD∥B1D1 , ∴ .
(2) ∵AO⊥BD , AO⊥PO ,
∴AO⊥面PBD ,
过点O作OM⊥PD于点M,连结AM ,
则AM⊥PD , ∴∠AMO 就是二面角A-PD-O的平面角,
又∵, ∴AP=,PO=
,
∴
,
即二面角的大小为
. -
21、解：
（1）设动点C（x,y）则D(x,0)。
因为H是CD的中点，故
因为
所以
故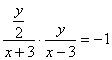
整理得动点C的轨迹方程
（2）设
并代入得
即
又原点O到直线l的距离为
当且仅当
即
时等号成立，故面积的最大值为
。
22、解：（1）当x=y=0时，
；令x=0，得
∴对任意的
故在（－1，1）上为奇函数.
（2）∵
满足
∴
∵
在（－1，1）上为奇函数.
∴
；
由
（3）
假设存在自然数m，使得对于任意
成立.
即
恒成立. ∴
解得
.
∴存在自然数，使得对于任意
成立.
此时，m的最小值为16.