2005年10月湖南省长沙县第三中学高三第二次月考试卷
数 学(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
制卷人:李铁
(满分150分 考试时间120分钟)
说明:本试卷在本校测试后平均分为71.6分,选择题5![]() 7
7![]() 8
8![]() 9
9![]() 10填空题14
10填空题14![]() 15解答题16
15解答题16![]() 20
20![]() 21丢分较多
21丢分较多![]()
一![]() 选择题(每小题5分,共50分)
选择题(每小题5分,共50分)
1![]() 如图,I是全集,M
如图,I是全集,M![]() P
P![]() S是I的子集,则阴影部分所表示的集合是( )
S是I的子集,则阴影部分所表示的集合是( )

A![]() (M∩P)∩S
(M∩P)∩S
B![]() (M∩P)∪S
(M∩P)∪S
C![]() (M∩P)∩(CIS)
(M∩P)∩(CIS)
D![]() (M∩P)∪(CIS)
(M∩P)∪(CIS)
2![]() 已知函数
已知函数![]() ,满足
,满足![]() ,则
,则![]() 的值是( )
的值是( )![]()
A![]() 5 B
5 B![]() -5 C
-5 C![]() 6 D
6 D![]() -6
-6
3![]() 设集合A=
设集合A=![]() ,B=
,B=![]() 满足A
满足A![]() B,则实数a的取值范围是(
)
B,则实数a的取值范围是(
)
A![]() [2,+
[2,+![]() B
B![]() (-∞,1
(-∞,1![]() C
C![]() [1,+
[1,+![]() D
D![]() (-∞,2
(-∞,2![]()
4![]() 函数
函数![]() 的反函数为
的反函数为![]() ,则
,则![]() 等于( )
等于( )
A![]() 1+2
1+2![]() B
B![]() -7
C
-7
C![]() 9
D
9
D![]() -7或9
-7或9
5.命题p:α是第二象限角,命题q:α是钝角,则p是q的 ( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
6![]() 设a<0,角α的终边经过点P(-3a,4a),那么sinα+2cosα的值等于 ( )
设a<0,角α的终边经过点P(-3a,4a),那么sinα+2cosα的值等于 ( )
A. ![]() B. -
B. -![]() C.
C. ![]() D. -
D. -![]()
7. 函数![]() 的定义域是
( )
的定义域是
( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
8![]() 有穷数列1,
有穷数列1,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 的项数是( )
的项数是( )
A![]() 3 n+7
B
3 n+7
B![]() 3 n +6
C
3 n +6
C![]() n +3
D
n +3
D![]() n +2
n +2
9.等比数列{an}中,已知a1+a2+a3=6,a2+a3+a4=-3,则a3+a4+a5+a6+a7+a8等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10![]() 函数
函数![]() 对于x
对于x![]() y∈R
y∈R![]() ,当x>0时
,当x>0时![]() ,且
,且![]() =4,则( )
=4,则( )
A![]()
![]() 在R上是减函数,且
在R上是减函数,且![]() =3 B
=3 B![]()
![]() 在R上是增函数,且
在R上是增函数,且![]() =3
=3
C![]()
![]() 在R上是减函数,且
在R上是减函数,且![]() =2 D
=2 D![]()
![]() 在R上是增函数,且
在R上是增函数,且![]() =2
=2
第Ⅱ卷(非选择题 共100分)
二![]() 填空题(本大题共5小题,每小题4分,共20分.把答案填在题中横线上)
填空题(本大题共5小题,每小题4分,共20分.把答案填在题中横线上)
11![]() 等差数列{
等差数列{![]() }中,若
}中,若![]() +
+![]() +
+![]() =15,
=15,![]() +
+![]() +
+![]() =3,则前9项的和
=3,则前9项的和![]() =
=
![]()
12![]()
![]() tan11°+
tan11°+![]() tan19°+tan11°·tan19°的值是____________.
tan19°+tan11°·tan19°的值是____________.
13![]() cos4
cos4 ![]() 等于__________.
等于__________.
14. 设函数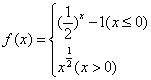 ,已知
,已知![]() ,则
,则![]() 的取值范围为______________.
的取值范围为______________.
15. 已知函数![]() ,则
,则![]() 的单调减区间是______________________.
的单调减区间是______________________.
三![]() 解答题(本大题共6小题,共80分.解答应写出文字说明
解答题(本大题共6小题,共80分.解答应写出文字说明![]() 证明过程或演算步骤)
证明过程或演算步骤)
16.(本小题满分13分)在下列两个坐标系中,分别画出所对应的函数的图象:
(1)![]() (2)
(2)![]()
(本题主要考查函数图像的伸缩平移对称变换 )
17.(本小题满分13分)已知sinα是方程![]() 的根,求
的根,求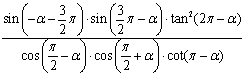 的值.(12分)
的值.(12分)
(本题主要考查诱导公式方程思想)
18.(本小题满分12分)试求函数y=sinx+cosx+2sinxcosx+2的最大值和最小值(12分)
(本题主要考查利用sinx+cosx与sinxcosx的关系,换元法求三角函数的最值)
19.(本小题满分13分)数列{![]() }是首项为23,公差为整数的等差数列,且第6项为正,第7项为负
}是首项为23,公差为整数的等差数列,且第6项为正,第7项为负![]()
(1)求数列{![]() }的公差;
}的公差;
(2)求前n项和![]() 的最大值;
的最大值;
(3)当![]() >0时,求n的最大值
>0时,求n的最大值![]()
(本题主要考查方程![]() 不等式与函数的思想数列中的应用)
不等式与函数的思想数列中的应用)
20.(本小题满分14分)已知定义在R上的函数![]() ,满足:
,满足:![]() ,且
,且![]() 时,
时,![]() ,
, ![]() .
.
(I)求证:![]() 是奇函数; (II)证明
是奇函数; (II)证明![]() 在R上是减函数
在R上是减函数![]()
(III)求![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
(本题借助抽象函数模型考查学生利用定义法研究函数的性质的能力)
21.(本小题满分14分)某工厂从今年起,若不改善生产环境,按现状生产,每月收入为70万元,同时将受到环保部门的处罚,第一个月罚3万元,以后每月递增2万元.如果从今年一月起投资400万元增加回收净化设备以改善生产环境(改造设备时间不计).按测算,新设备投产后的月收入与时间的关系如图所示.
(Ⅰ)设g(n)表示投资改造后的前n个月的总收入,写出g(n)的函数关系式;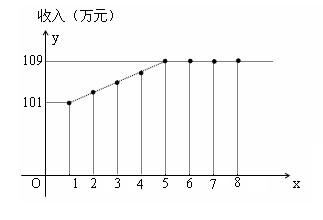
(Ⅱ)问经过多少个月,投资开始见效,即投资改造后的月累计纯收入多于不改造时的月累计纯收入?
(本题是一道与图表有关的数列的综合应用题,目的是考查学生的综合解题能力)
2005年10月长沙县第三中学高三第二次月考试卷答卷
一、选择题(每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二![]() 填空题(本大题共5小题,每小题4分,共20分.把答案填在下面题号对应的横线上)
填空题(本大题共5小题,每小题4分,共20分.把答案填在下面题号对应的横线上)
11._________ 12._________ 13.__________ 14.________________ 15_____________.
三![]() 解答题(本大题共6小题,共80分.解答应写出文字说明
解答题(本大题共6小题,共80分.解答应写出文字说明![]() 证明过程或演算步骤)
证明过程或演算步骤)
16(本小题满分13分)在下列两个坐标系中,分别画出所对应的函数的图象:
(1)![]() (2)
(2)![]()
 |  |
(1) (2)
17.(本小题满分13分)
18.(本小题满分13分)
19.(本小题满分13分)
20.(本小题满分14分)
21.(本小题满分14分)
参考答案
1-5CCACB,6-10ADCAD
11![]() 27
27
12![]() 1
1
13![]()
![]()
14![]()
![]() 或
或![]()
15![]()
![]()
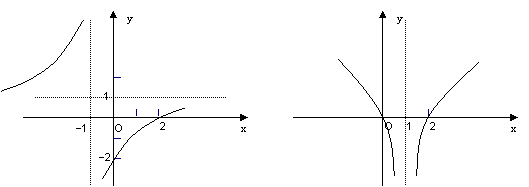 16
16![]() 解:(1)
解:(1)![]() (2)
(2)![]()
(1) (2)
17提示: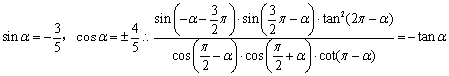 =
=![]()
18![]()
![]()
19![]() 解:(1)数列{
解:(1)数列{![]() }中,
}中,![]() =23,
=23,![]() >0,
>0,![]() <0,公差d∈Z,
<0,公差d∈Z,
则![]() ∴
∴![]() ,
,
∵公差d∈Z,∴d=-4![]()
(2)等差数列{![]() }中,
}中,![]() =23,d=-4,
=23,d=-4,
∴![]() ,
,
当n=6时,![]() 有最大值为
有最大值为![]() =78
=78![]()
(3)∵![]() ,又n>0,∴n<12.5,
,又n>0,∴n<12.5,
∴![]() >0时,n的最大值为12
>0时,n的最大值为12![]()
20![]() 证明略
证明略![]()
21![]() 解(Ⅰ)设
解(Ⅰ)设![]() 表示第
表示第![]() 个月的收入,则由图得a 1 =101,a 5 =109,且数列{ai}的前五项是公差为2的等差数列,第六项开始是常数列,
个月的收入,则由图得a 1 =101,a 5 =109,且数列{ai}的前五项是公差为2的等差数列,第六项开始是常数列,
所以
g(n)=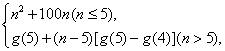
即g(n)= 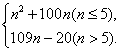
(Ⅱ)不改造时的第n个月累计纯收入: ![]() ,投资改造后的第n个月累计纯收入:
,投资改造后的第n个月累计纯收入:
(1)当n≤5时,纯收入为![]() +100n-400,由
+100n-400,由![]() +100n-400>
+100n-400>![]() ,
,
解得n>-8 +![]() ,由-8+
,由-8+![]() >-8 +
>-8 +![]() =8,得n>8,即前5个月不效.
=8,得n>8,即前5个月不效.
(2)当n>5时,纯收入(109n-20)-400,由(109n-20)-400>![]() ,得
,得
![]() ,解得:
,解得:![]()
而n=9适合上述不等式.
所以,必须经过8个月后,即第9个月才见效.