高考天津市和平区高三调研试卷数学

天津市和平区2005—2006学年度高三调研试卷

数　 学

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。满分150分，考试时间120分钟。

第Ⅰ卷（选择题　共60分）

一、选择题（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）

1．已知集合M=，N=，那么MN等于

A．（0,1），（1,2）　　　　　　　　　　　　B．｛（0,1），（1,2）｝　

C．｛y︱y=1或y=2｝　　　　　　　　　　　D．｛y︱y1｝

2．（理）f（x）=，若f（x）f（3.5），则不等式的解集为

A．（0，）（1，）　　　　　　　　 B．（，+）

C．（0，）（，+）　　　　　　　 D．（，）

（文）不等式组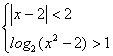的解集为

A．（0，）　　　　B．（，2）　　　　C．（，4）　　　　D．（2，4）

3．已知数列｛a_n｝前n项和S_n=aⁿ－1（a0），那么｛a_n｝是

A．一定是等比数列　　　　　　　　　　　 B．一定是等差数列

C．或是等差数列或是等比数列　　　　 　　D．既非等差数列又非等比数列

4．已知集合A=｛1,2,3,4｝，集合B=｛－1,2｝，设映射f：AB，如果集合B中的元素都是A中元素的f下的象，那么这样的映射f有

A．16个　　　　　　 B．14个　　　　　　 C．12个　　　　　　 D．8个

5．条件甲：“a1”是条件乙：“a”的

A．既不充分又不必要条件　　　　　　　　 B．充要条件

C．充分不必要条件　　　　　　　 　　　　D．必要不充分条件

1	2
0.5	1
	a
		b
			c

6．在如图所示的表格中，每格填上一个数字后，使每一横行成等差数列，每一纵行成等比数列，则a+b+c的值为 天星 教育网

A．1　　　　B．2　　　　C．3　　　　　　D．

7．已知关于x的方程lg²x－2algx+2－a=0的两根均大于1，则a的取值　 范围是

A．(－,1)　　　　 　　B．[1,2]　　　　

C．[1,2]　　　　　　　　D．[2,+ )

8.（理）函数y=（x0）的反函数是

A．y=　　　　　　　　B．y=－

C．y=　　　　　　　　 D．y=－

（文）函数y=的反函数是

A．y=1+　　　　B．y=1+

C．y=1－　　　　　 D．y=1－

9．若a1，且a^－x+log_a^ya^－y+log_a^x，则x，y之间的大小关系是

A．xy0　　　　　B．x=y0　　　　　 C．yx0　　　　　D．不能确定

10．（理）数列｛a_n｝满足 a_n+1=，若a₁=，则a₂₀₀₅的值为

A．　　　　　　　 B．　　　　　　　 C．　　　　　　　 D．

（文）在数列｛a_n｝中，a₁=2，a_n+1=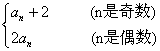，则a₅等于

A．12　　　　　　　 B．14　　　　　　　 C．22　　　　　　　 D．20

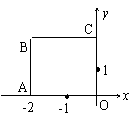11．若函数y=x²（x[a，b]）的值域为[0,4]，则点（a，b）的轨迹是图中的

A．线段BC和OA　　　　　B．线段AB和BC

C．线段AB和OC　　　　　D．点A（－2,0）和C（0,2）

12．给定实数x，定义[x]为不大于x的最大整数，则下列结论不正确的是 天星　教育网

A．x－[x]0　　　　　　　　B．x－[x]1　　　　

C．x－[x]是周期函数　　 D．x－[x]是偶函数

第Ⅱ卷（非选择题  共90分）

二、填空题（本大题共4小题，每小题4分，共16分，把答案填在题中横线上）

13．f（x）=－x²+ax+b²－b+1，对任意xR，f（1+x）=f（1－x）成立，若x[－1，1]时，f（x）0恒成立，则b的取值范围为　　　　　　　  。

14．函数y=的定义域为　　　　　　　

15．已知等差数列｛a_n｝的公差d0，且a₁,a₃,a₉成等比数列，则=　　　　　

16．已知命题P：不等式解集为R，命题q：f（x）=－（5－2m）^x是减函数，若p或q为真命题，p且q为假命题，则m的取值范围是　　　　　　　

三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）

17．（本小题满分12分）

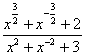已知x+x=3，求的值。

天星 教育网

18．（本小题满分12分）

已知数列｛a_n｝为等差数列（公差d0），｛a_n｝中的部分项组成的数列a_k1，a_k2，…，a_kn，…恰为等比数列，且其中k₁=1，k₂=5，k₃=17，求k₁+k₂+k₃+…+k_n

19．（本小题满分12分）

已知二次函数f（x）的二次项系数为a，且不等式f（x）－2x的解集为（1，3）。

（1）若方程f（x）+6a=0有两个相等的实根，求f（x）的解析式。

（2）若f（x）的最大值为正数，求a的取值范围。

20．（本小题满分12分）

已知f（n）=，且不等式f（n）log_a^（a－1）+，对一切大于1的自然数n成立，求实数a的范围。

21．（本小题满分12分）

设f（x）=log_a的定义域为[m，n]，值域为[log_a^a（n－1）,log_a^a（m－1）]

（1）求证：m2　　　　　

（2）求实数a的取值范围

22．（本小题满分14分）

（理）已知正项数列｛a_n｝满足a₁=a（0a1）且f（x）=又a_n+1f（a_n）（n1且nN）求证：

（1）a_n　　　　　 

（2）+…+1

（文）已知数列｛a_n｝，a₁=1，前n项和为S_n，对于任意的n2，nN₊，S_n-1－8,a_n，8S_n－4恒为等差数列

（1）求a₂，a₃，a₄

（2）证明：在n2时，数列｛a_n｝为等比数列。

参考答案

1—12　 D理（C）文（D） CBB　 DBBAD　BD

13、b－1或b　　 14、[－，0)(，1]　　 15、　　 16、1m2

17、由x+x =3可知　　　

x+x^－1=（x+x）²－2=7

x²+x^－2=（x+x^－1）²－2=47

x+x=（x+x）（x－1+x^－1）=18

原式=

18、由a₁，a₅，a₁₇成等比数列可得a₅²=a₁a₁₇

（a₁+4d）²=a₁（a₁+16d），又d0

a₁=2d

设等比数列｛k_n｝的公比为q，则q==3

a_kn=a₁·3^n－1又a_kn=a₁+（k_n－1）d

2d·3^n－1=2d+（k_n－1）d

k_n=2·3^n－1－1

k₁+k₂+…+k_n=2（3⁰+3¹+…+3^n－1）－n =2·－n=3ⁿ－n－1

19、（1）f（x）+2x0的解集为（1,3），

　　　　设f（x）+2x=a（x－1）（x－3），且a0，因而

　　f（x）=a（x－1）（x－3）－2x=ax²－（2+4a）x+3a　 ①

由方程f（x）+6a=0得ax²－（2+4a）x+9a=0　　  　 ②

方程②有两个相等的实根

　　=[－（2+4a）]²－4a×9a=0

　　即5a²－4a－1=0解得a=1或a=－

　　由于a0　　a=－代入①得f（x）的解析式

　　f（x）=－x²－x－

（2）由f（x）=ax²－2（1+2a）x+3a =a（x－）²－

又a0，可得f（x）的最大值为－

由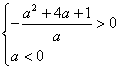解得a或－2+0

故当f（x）的最大值为正数时，实数a的取值范围是

（－，－2－）（－2+，0）

20、f（n）=+…+

f（n+1）－f（n）

　　=（）－（）

　　　=

　　　= =0

f（n）是关于n的递增函数（或者可说数列｛f（n）｝是递增数列）

f（n）f（z）=

要使f（n）（n2）恒成立

f（z）

 －1

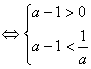
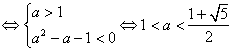
故实数a的范围为：

21、（1）依题意知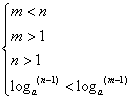

　　　　mn　　　　　m－1n－1

0

由可得x－2或x2

[m,n]（2,+）

m2

（2）由①知0　　f（u）=log_a^u在（0,+）上单调递减

而u（x）=在[m,n]上单调递增

又f（x）的值域为[log_a,log_a]

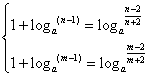
即m,n为方程1+log_a=log_a在（2,+）内的两个不相等的实根，

即方程ax²+（a－1）x－2a+2=0在（2,+）内有两个不相等的实根

令f（x）=ax²+（a－1）x－2a+2，则

有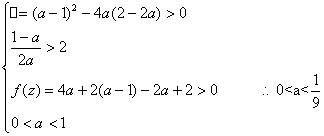

故所求实数a的取值范围为：0

天星　教育网

22、（理）证明：（1）f（x）=，a_n+1f（a_n）

a_n+1　　

由叠加可知

而a₁=a，则a_n

（2）0a1及a_n可知

a_n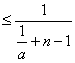

从而

成立

（文）（1）S_n－1－8，a_n，8S_n－4成等差数列

2a_n=8S_n+S_n－1－12=9S_n－a_n－12

即a_n=3S_n－4（n2）　　　　  　　　　①

由a₁=1求得a₂=, a₃=－, a₄=

（1）由①式可知a_n+1=3S_n+1－4　　　　  ②

②－①得　a_n+1－a_n=3a_n+1

又a₂=0

由等比数列的定义可知在n2时，｛a_n｝为等比数列。