天津市河西区2005—2006学年度第一学期高三年级统一调研模拟试卷
数学
第Ⅰ卷(共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.与直线![]() 平行的曲线
平行的曲线![]() 的切线方程是( )
的切线方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.设![]() ,其中
,其中![]() 是大于1的正整数,若
是大于1的正整数,若![]() ,
,![]() ,则
,则![]() 的取值集合是( )
的取值集合是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知![]() ,则
,则![]() 的解析式可取为( )
的解析式可取为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知数列![]() 中,
中,![]() ,
,![]() ,且满足
,且满足![]() (
(![]() ),则
),则![]() ( )
( )
A.16 B.![]() C.32 D.
C.32 D.![]()
5.若![]() ,则下列不等式:①
,则下列不等式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 中,正确的不等式有( )
中,正确的不等式有( )
A.1个 B.2个 C.3个 D.4个
6.已知![]() 、
、![]() 是非零向量且满足
是非零向量且满足![]() ,
,![]() ,则
,则![]() 与
与![]() 的夹角是( )
的夹角是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.从4名男生和5名女生中任意选出3人参加一个会议,其中至少有1名男生和一名女生,则不同的选派方案有( )
A.140种 B.84种 C.70种 D.35种
8.铜质的球体由于温度的变化,其半径增加了![]() ,则它的体积约增加了( )
,则它的体积约增加了( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.函数![]() 和函数
和函数![]() 的图像的交点个数为( )
的图像的交点个数为( )
A.0 B.1 C.2 D.3
10.设全集![]() ,集合
,集合![]() ,集合
,集合![]() ,那么点
,那么点![]() 的充要条件是(
)
的充要条件是(
)
A.![]() 或
或![]() B.
B.![]() 且
且![]()
C.![]() 或
或![]() D.
D.![]() 且
且![]()
11.定义在区间![]() (
(![]() )上的函数
)上的函数![]() 的值域是
的值域是![]() ,则
,则![]() 的最大值
的最大值![]() 和最小值
和最小值![]() 分别是( )
分别是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.若![]() ,定义:
,定义:![]() ,例如:
,例如:![]() ,则函数
,则函数![]() 的奇偶性是( )
的奇偶性是( )
A.是偶函数不是奇函数 B.是奇函数不是偶函数
C.既是奇函数又是偶函数 D.既不是奇函数又不是偶函数
第Ⅱ卷(共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上。
13.不等式![]() 的解集是
。
的解集是
。
14.凸多面体是由4个三角形和5个四边形围成,则其顶点数是 。
15.
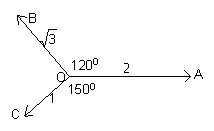
如图,向量![]() 、
、![]() 、
、![]() 的长度分别是2、
的长度分别是2、![]() 、1,
、1,![]() 、
、![]() ,则
,则![]()
![]() +
+ ![]() 。
。
16.某工厂生产A、B、C三种不同型号的产品,产品数量之比依次为![]() ,现用分层抽样方法抽出一个容量为
,现用分层抽样方法抽出一个容量为![]() 的样本,样本中A种型号产品有16件.那么此样本的容量
的样本,样本中A种型号产品有16件.那么此样本的容量![]() =
。
=
。
三、解答题:本大题共6小题,共74分. 解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
函数![]() (其中
(其中![]() 、
、![]() )的图像经过三点
)的图像经过三点![]() 、
、![]() 、
、![]() 。
。
(1)求![]() 的值;
的值;
(2)是否存在常数![]() ,使
,使![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() ,若不存在,说明理由。
,若不存在,说明理由。
18.(本小题满分12分)
设棋子在正四面体![]() 的表面从一个顶点移向另外三个顶点是等可能的。现抛掷骰子根据其点数决定棋子是否移动:若投出的点数是奇数,则棋子不动;若投出的点数是偶数,棋子移动到另一顶点。若棋子的初始位置在顶点
的表面从一个顶点移向另外三个顶点是等可能的。现抛掷骰子根据其点数决定棋子是否移动:若投出的点数是奇数,则棋子不动;若投出的点数是偶数,棋子移动到另一顶点。若棋子的初始位置在顶点![]() ,回答下列问题。
,回答下列问题。

(1)投了2次骰子,棋子才到达顶点![]() 的概率是多少?
的概率是多少?
(2)投了3次骰子,棋子恰巧在顶点![]() 的概率是多少?
的概率是多少?
19.(本小题满分12分)
设函数![]() (常数
(常数![]() 且
且![]() )的定义域是
)的定义域是![]() 。如果对于定义域内的每一个
。如果对于定义域内的每一个![]() ,都有
,都有![]() ,那么
,那么![]() 。
。
(1)证明上述命题;
(2)写出上述命题的逆命题。若逆命题正确,请加以证明;若逆命题不正确,请举出一个反例说明。
20.(本小题满分12分)
如图,在棱长为1的正方体ABCD—A1B1C1D1中,
(1)线段![]() 上是否存在一点
上是否存在一点![]() 使得
使得![]() 平面
平面![]() ,若存在,确定
,若存在,确定![]() 点的位置,若不存在,说明理由;
点的位置,若不存在,说明理由;
(2)点![]() 在线段
在线段![]() 上,若二面角
上,若二面角![]() 的大小是
的大小是![]() ,求
,求![]() 的长;
的长;
(3)点![]() 在对角线
在对角线![]() 上,使
上,使![]() 平面
平面![]() ,求
,求![]() 。
。

21.(本小题满分12分)
已知定点![]() ,定直线
,定直线![]() ,动直线
,动直线![]() (其中
(其中![]() )。
)。
证明:(1)动直线![]() 上一定存在相异两点
上一定存在相异两点![]() ,它们到点
,它们到点![]() 与到直线
与到直线![]() 的距离相等;
的距离相等;
(2)对(1)中的相异两点![]() ,证明:
,证明:![]() ;
;
(3)对(1)中的相异两点![]() ,以
,以![]() 为焦点的动椭圆经过坐标原点
为焦点的动椭圆经过坐标原点![]() ,设动椭圆的离心率是
,设动椭圆的离心率是![]() ,证明:
,证明:![]() 。
。
22.(本小题满分14分)
数列![]() 的前
的前![]() 项和
项和![]() (
(![]() ),且
),且![]() ,
,![]() (
(![]() )。
)。
(1)求数列![]() 的通项;
的通项;
(2)已知定理:“若函数![]() 在区间
在区间![]() 上是凹函数,
上是凹函数,![]() ,且
,且![]() 存在,则有
存在,则有![]() ”。若函数
”。若函数![]() (
(![]() )在
)在![]() 上是凹函数,试判断
上是凹函数,试判断![]() 与
与![]() 的大小;
的大小;
(3)求证:![]() 。
。
数学答案
一、选择题:BDCD CACC CCCA
二、填空题:13.![]() ;14.9;15.
;14.9;15.![]() ;16.72。
;16.72。
三、解答题:
17.(1)由已知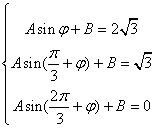 ……2分,
……2分,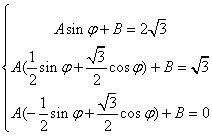 ……4分,解得
……4分,解得![]() ……8分;
……8分;
(2)由![]() ,故存在
,故存在![]() 使
使![]() 恒成立……12分。
恒成立……12分。
18.棋子从顶点![]() 移动到顶点
移动到顶点![]() 的概率都是
的概率都是![]() ,而不移动的概率是
,而不移动的概率是![]() ……2分。(1)分两种情形:①第一次不动,第二次移到
……2分。(1)分两种情形:①第一次不动,第二次移到![]() ,即
,即![]() ;……4分,②两次都动,即
;……4分,②两次都动,即![]() 或
或![]() ,故投了2次骰子,棋子才到达顶点
,故投了2次骰子,棋子才到达顶点![]() 的概率是
的概率是![]() ……6分。
……6分。
(2)①两次停在相同顶点:![]() 、
、![]() 、
、![]() ;②一次停在相同的点:
;②一次停在相同的点:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ;③每次都向其它顶点移动:
;③每次都向其它顶点移动:![]() 、
、![]() 、
、![]() 、
、![]()
![]() 、
、![]() 。……10分
。……10分
所以投三次骰子,棋子恰巧在顶点![]() 的概率是
的概率是![]() 。……12分
。……12分
19.(1)因为![]() 时都有
时都有![]() ,故
,故![]() ……2分,当
……2分,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,即总有
,即总有![]() ……4分,因为
……4分,因为![]() 所以
所以![]() ,即
,即![]() ……6分;
……6分;
(2)逆命题是:设函数![]() (常数
(常数![]() 且
且![]() )的定义域是
)的定义域是![]() 。如果
。如果![]() ,那么对于定义域内的每一个
,那么对于定义域内的每一个![]() ,都有
,都有![]() 。……9分,此逆命题是错误的。容易构造例子:
。……9分,此逆命题是错误的。容易构造例子:![]() 时,
时,![]() ,但是
,但是![]() ,所以逆命题错误。……12分
,所以逆命题错误。……12分

20.(1)如图,若点![]() 存在,由
存在,由![]() 平面
平面![]() ,得
,得![]()
![]() ,因为
,因为![]() ,所以
,所以![]() ,这与
,这与![]() 是正三角形矛盾,故点
是正三角形矛盾,故点![]() 不存在;……4分
不存在;……4分

(2)过![]() 作
作![]() 垂足为
垂足为![]() ,连
,连![]() ,由于
,由于![]() 平面
平面![]() ,故
,故![]() ,
,![]() 是二面角
是二面角![]() 的平面角,
的平面角,![]() ,即
,即![]() ,
,![]() ,在
,在![]() 中,由正弦定理
中,由正弦定理![]() ,故
,故![]() ;……8分
;……8分
(3)由于![]()
![]() ,所以
,所以![]() 平面
平面![]() ,点
,点![]() 是直线
是直线![]() 与平面
与平面![]() 的交点。易见
的交点。易见![]() ∽
∽![]() ,所以
,所以![]() 。……12分
。……12分
21.(1)到点![]() 与到直线
与到直线![]() 的距离相等的点的轨迹是抛物线,方程为
的距离相等的点的轨迹是抛物线,方程为![]() ,由方程组
,由方程组![]() ,即
,即![]() ,因为
,因为![]() ,且
,且![]() ,故方程组有两组不同的解,即直线
,故方程组有两组不同的解,即直线![]() 上一定存在相异两点
上一定存在相异两点![]() ,它们到点
,它们到点![]() 与到直线
与到直线![]() 的距离相等;……4分
的距离相等;……4分
(2)设![]() 、
、![]() ,显然
,显然![]() 都是非零向量,要证
都是非零向量,要证![]() ,只要证
,只要证![]() ,即
,即![]() ,而
,而![]() 、
、![]() ,即证
,即证![]() ,即
,即![]() ,由(1)
,由(1)![]() 是方程
是方程![]() 的两根,即
的两根,即![]() ,
,![]() ,此时
,此时![]() ,故
,故![]() ,即
,即![]() ;……8分
;……8分
(3)动椭圆长轴![]() ,焦距
,焦距![]() ,故
,故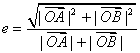 ,
,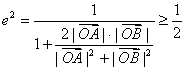 (当且仅当
(当且仅当![]() 时取等号),由于直线
时取等号),由于直线![]() 与
与![]() 轴不垂直,故
轴不垂直,故![]() ,所以
,所以![]() 。……12分
。……12分
22.(1)![]() 时,
时,![]() ,
,![]() ;
;![]() 时,
时,![]() ,所以有
,所以有![]() ,即
,即![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() 。综上
。综上![]() 。5分
。5分
(2)由于![]() ,根据
,根据
![]()
令![]() ,可得
,可得![]()
![]()
![]() ;……10分
;……10分
(3)由于![]() ,所以
,所以![]() ,又由(2)
,又由(2)![]() ,故
,故![]() 。……14分
。……14分