增城市高级中学普通毕业班综合测试四
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.
1、若集合
，则
= （ ）
A、
B、
C、
D、
2、若奇函数
的定义域为
，则有 （ ）
A、
B、
C、
D、
3、若
是异面直线，且
//平面
，那么
与平面的位置关系是 （ ）
A、
B、与相交 C、
D、以上三种情况都有可能
4、已知等比数列
的前
项和
，则
等于 （ ）
A、
B、
C、
D、
5、某校高中生共有2400人，其中高一年级900人，高二年级700人，高三年级800人，现采用分层抽取容量为48的样本，那么高一，高二，高三年级抽取的人数分别为（ ）
A、24，8，16 B、16，16，16 C、14，16，18 D、18，14，16
6、若函数满足
，则的解析式在下列四式中只可能是 （ ）
A、
B、
C、
D、
7、圆
截直线
所得弦长等于 （ ）
A、
B、
C、1 D、5
8、若随机变量
的分布列如下表，则
的值为 （ ）
|
| 0 | 1 | 2 | 3 | 4 | 5 |
| P | 2 | 3 | 7 | 2 | 3 |
|
A、
B、
C、
D、
9、若直线
与圆
有两个不同的公共点，则实数的取值范围是（ ）
A、
B、
C、
D、
10、我国发射的“神舟5号”宇宙飞船的运行轨道是以地球的中心
为一个焦点的椭圆，近地点
距地面为
千米，远地点
距地面为千米，地球半径为千米，则飞船运行轨道的短轴长为（ ）
A、
B、
C、
D、
11、某校有6间不同的电脑室，每天晚上至少开放2间，欲求不同安排方案的种数，现有四位同学分别给出下列四个结果：①
；②
；③
；④
。其中正确的结论是（ ）
A、仅有① B、仅有② C、②和③ D、仅有③
12、将函数
的图像按向量
平移后得到函数
的图像，给出以下四个命题：①的坐标可以是
；②的坐标可以是
；③的坐标可以是或；④的坐标可以有无数种情况。其中真命题的个数是 （ ）
A、1 B、2 C、3 D、4
二、填空题：把答案填在题中横线上.
13、已知函数
，则
=
.
14、已知正方体
，则该正方体的体积与该正方体的外接球的体积之比为 .
15、在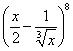
的展开式中，常数项是
.
16、已知函数
在区间
上是增函数，则实数的取值范围是
.
三、解答题：解答应写出文字说明，证明过程或演算步骤.
17、已知函数
（1）若
，求的单调递增区间；
（2）若
时，的最大值为4，求的值，并指出此时
的值。
18、设两个向量
，满足
的夹角为
，若向量
与向量
的夹角为钝角，求实数
的取值范围。
19、如图正方体中，
分别是
的中点，
（1）证明
；
（2）证明
平面
；
（3）求
。
20、若对于某个数学问题，甲解出此题的概率是
，乙解出此题的概率是
，设解出此题的人数为
21、已知数列中，
，数列
满足
（1）求证数列是等差数列；
（2）求数列中的最大项与最小项，并说明理由；
（3）记
，求
。
22、设双曲线
的离心率为
，若右准线
与两条渐进线相交于
两点，
为右焦点，
为等边三角形。
（1）求双曲线
的离心率的值；
（2）若双曲线被直线
截得的弦长为
，求双曲线的方程。
高级中学2004届普通毕业班综合测试四参考答案
一、选择题： DCDDD CACBA CD
二、填空题：13、
14、
15、7 16、
三、解答题：17、解：（1）
解不等式 
得
∴的单调递增区间为
（2）∵
，∴
，∴当
即
时，有最大值
， ∵
，∴
，此时。
18、解：
欲使夹角为钝角，需
设
即
时，向量与的夹角为
∴夹角为钝角时，的取值范围是
。
19、解：以
为轴、以
为
轴、以
为
轴建立空间直角坐标系，设正方体棱长为，则
（1）
，
∵
，∴
（2）
∵
，∴面。
（3）由
|
| 0 | 1 | 2 |
|
|
|
|
|
∴
。
20、解：解出此题的分布列为
∴
，
21、解：（1）
，∴是以
，公差为1的等差数列。
（2）
，对于函数
，在
时，
，在
上为减函数，故当
时，
取得最大值
.
而函数，在
时，
，在
上为减函数，故当
时，取得最小值
.
（3）
22、（1）右准线的方程为：
，渐近线方程为：
，交点坐标为
，
∵
为正三角形，∴
（2）由（1）得双曲线方程为
，将
代入得
∴弦长
，∵
或
，
∴双曲线的方程为：
或
。